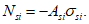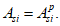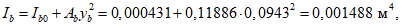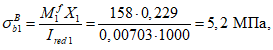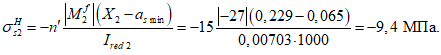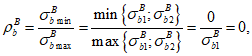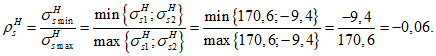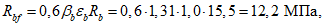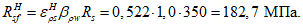СВЕДЕНИЯ О ДОКУМЕНТЕ
Источник публикации
М., 2017
Примечание к документу
Название документа
"Методическое пособие. Методические рекомендации по применению СП 35.13330.2011 "СНиП 2.05.03-84* "Мосты и трубы"
"Методическое пособие. Методические рекомендации по применению СП 35.13330.2011 "СНиП 2.05.03-84* "Мосты и трубы"
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ПРИМЕНЕНИЮ СП 35.13330.2011
"СНиП 2.05.03-84* "МОСТЫ И ТРУБЫ"
Настоящие Методические рекомендации к
СП 35.13330
"Мосты и трубы" разработаны в соответствии с планом НиОКР ФАУ ФЦС Минстроя РФ на 2017 год. Работа выполнена ГУП "Институт Промтрансниипроект" и ООО "Научно-исследовательский институт мостовых и гидротехнических сооружений (НИИ "МИГС") с привлечением специалистов АО ЦНИИС, Мостотреста, ОАО Гипростроймост.
В нашей стране и за рубежом накоплен значительный опыт в создании методических пособий и рекомендаций, разъясняющих и дополняющих нормативные требования к строительным конструкциям. Можно указать в качестве примера "
Пособие
по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003)".
Одной из форм изложения такого рода документов является принятая в нормах проектирования автодорожных мостов AASHTO (США) система, при которой каждая страница разделена вдоль на две половины - в левой половине содержатся нормативные положения, а в правой - разъяснения и комментарии с ссылками на соответствующие исследования.
Строительные нормы, в силу их ограниченного объема, не могут охватить все возможные конструктивные и технологические решения, нюансы проектирования, допускают иногда двойное толкование. Методические рекомендации к сводам правил призваны восполнить эти пробелы. Они помогают проектировщикам выполнять обязательные нормативные требования, могут содержать альтернативные решения, оптимизируют процесс проектирования.
Такие же цели преследуют настоящие Методические рекомендации применительно к проектированию железобетонных мостовых сооружений.
Представляется целесообразным разработать аналогичные документы ко всем разделам
СП 35.13330
.
Следует отметить, что отсутствие методических рекомендаций к сводам правил невозможно восполнить ведомственными документами, которые апробируются на более низком уровне в разных ведомствах и порой противоречат один другому.
Методические рекомендации подготовлены: к.т.н. А.С. Бейвелем, д.т.н. А.И. Васильевым, к.т.н. Б.И. Кришманом (ООО "НИИ МИГС"); инж. Ф.В. Винокуром (ООО "ИЦМИТ"); инж. А.С. Малофеевым (ОАО "Институт Гипростроймост"); к.т.н. Ю.В. Новаком (НИЦ Мосты ОАО ЦНИИС).
Настоящие Методические рекомендации к
СП 35.13330
"Мосты и трубы" используются при проектировании мостовых железобетонных конструкций, на которые распространяется действие
СП 35.13330
.
В данном пункте приведен перечень нормативных документов, которые используются в настоящих Методических рекомендациях, но не вошли в
Приложение А
к СП 35.13330. Остальные нормативные ссылки следует смотреть в
Приложении А
к СП 35.13330.
ГОСТ 33178-2014
. Дороги автомобильные общего пользования. Классификация мостов.
ГОСТ 27751-2014
. Надежность строительных конструкций и оснований. Основные положения.
ГОСТ 24452-80
. Бетоны. Методы испытаний.
ГОСТ 18322-78
. Системы технического обслуживания и ремонта техники. Термины и определения.
ГОСТ 10180-90
. Бетоны. Методы определения прочности по контрольным образцам.
EN 10138-3.2009. Prestressing steels. Strend.
ГОСТ 25192-82
. Бетоны. Классификация и общие технические требования.
СП 131.13330.2012
. Строительная климатология.
Настоящие Методические рекомендации к
СП 35.13330
разъясняют, дополняют, развивают те положения
раздела 7
"Бетонные и железобетонные конструкции", которые, по мнению авторов, нуждаются в такого рода комментариях.
Методические рекомендации включают разделы, содержащие комментарии к указаниям
СП 35.13330
по основным расчетным требованиям, материалам, расчетам, конструированию мостовых железобетонных конструкций.
Для связи предлагаемых рекомендаций и разъяснений с текстом
СП 35.13330
в заголовках к пунктам Методических рекомендаций приводятся номера соответствующих пунктов Свода правил.
В разделах Методических рекомендаций
2
-
5
, относящихся к расчетам железобетонных конструкций, предлагается измененная по сравнению с
СП 35.13330
последовательность изложения материала. Расчеты группируются не по их видам (прочность, выносливость, трещиностойкость), а по характеру работы рассчитываемых конструктивных элементов (изгибаемые, внецентренно сжатые и т.д.). Такая последовательность в большей степени соответствует методике проектирования железобетонных конструкций. При этом все виды расчетов, выполнение которых требуется в
СП 35.13330
, нашли свое отражение в Методических рекомендациях.
Целью Методических рекомендаций является развитие и разъяснение ряда положений расчетов и конструирования железобетонных мостов, которые в СП недостаточно освещены или имеют неоднозначную трактовку.
Применение Методических рекомендаций позволит более точно и рационально выполнить требования
СП 35.13330
, а в некоторых случаях застраховать конструкторов от ошибок, вызванных неточностями и недоработками действующего СП.
При составлении настоящих рекомендаций авторами проанализирована эффективность применения на практике тех или иных проектных решений на основе опыта обследований и испытаний, мониторинга технического состояния, а также научно-технического сопровождения работ по монтажу и предварительному напряжению мостовых железобетонных конструкций.
1.4.1 Дополнительные термины и определения, которые используются в тексте
СП 35.13330
и в настоящих Методических рекомендациях, составлены с учетом указаний нормативных документов [
1
,
2
], основные положения которых сводятся к следующим:
- термин является коротким наименованием объекта (слово), существенные свойства (признаки) которого отражены в определении к термину;
- определение
<1>
[3]
, описывающее термин, должно быть кратким, включать существенные конструктивные признаки, характеризующие данный объект, не должно выражаться через термин или его повторять, а все слова в составе определения должны иметь однозначную трактовку;
- указание на функциональное назначение объекта в составе определения не является существенным признаком, характеризующим объект.
--------------------------------
<1> Определение - это формулировка, разъясняющая смысл термина и являющаяся техническим образом, фиксирующим существенные признаки и взаимосвязь предметов, в этот образ входящих.
1.4.2 В тексте
СП 35.13330
имеются положения, допускающие отклонения от основных требований. Такие положения обычно содержат термины "как правило", "рекомендуется", "допускается", под которыми понимается следующее
[4]
:
- "как правило" - такое требование является преобладающим, а отступление от него должно иметь обоснование;
- "допускается" - данное решение применяется в виде исключения как вынужденное;
- "рекомендуется" - данное решение является одним из лучших, но не обязательным.
1.4.3 При работе с текстом
СП 35.13330
рекомендуется применять нижеприведенные термины и определения, а также условные обозначения, составленные с учетом определений, в
ГОСТ 27751
, данных в
ГОСТ 24452
,
ГОСТ 18322
, а также документах [
5
-
7
].
Общие термины
Предельное состояние:
состояние, при котором конструкция или сооружение перестают удовлетворять проектным потребительским свойствам.
Примечание: к предельным состояниям
первой группы
относятся в том числе: потеря устойчивости формы и положения; хрупкое или вязкое разрушение; усталостное разрушение; разрушение от совместного воздействия силовых факторов и неблагоприятных влияний внешней среды.
К предельным состояниям
второй группы
относятся состояния, затрудняющие, делающие невозможным нормальную эксплуатацию конструкций или снижающие их долговечность вследствие появления недопустимых перемещений (прогибов, осадок, углов поворота), колебаний и трещин.
Грузоподъемность:
потребительское свойство, определяющее максимально допустимые весовые параметры транспортных средств и пешеходного движения, а также режимы их пропуска по мосту.
Обеспеченность:
вероятность благоприятной реализации значения переменной случайной величины с превышением значений для характеристик материалов и непревышением заданного значения для нагрузок.
Нормативный документ:
фиксированная, доступная широкому кругу потребителей информация, законодательно устанавливающая правила, общие принципы и характеристики определенных видов деятельности в области строительства и их результатов.
Конструкционный бетон:
бетон, к которому предъявляются требования по механическим свойствам и долговечности.
Конструктивные элементы
Железобетонный мост:
сооружение, содержащее опоры и перекрывающие пространство между ними железобетонные пролетные строения, предназначенное для пропуска подвижной нагрузки и коммуникаций через препятствия над: реками - мосты, ущельями - виадуки, дорогами - путепроводы, застройками и подходами - эстакады, для пропуска водных потоков - акведуки.
Пролетное строение:
несущая конструкция моста, перекрывающая пространство между опорами, воспринимающая постоянную и временную нагрузки и передающая их на опоры.
Опора:
несущий элемент мостового сооружения, поддерживающий пролетное строение и передающий нагрузки на фундамент.
Мостовое полотно:
совокупность всех элементов, расположенных на плите проезжей части пролетных строений, предназначенных для обеспечения безаварийных условий движения транспортных средств и пешеходов, а также отвода воды с проезжей части.
Примечание: мостовое полотно включает в себя одежду ездового полотна (в т.ч. покрытие и гидроизоляцию), тротуары, ограждающие устройства, устройства для водоотвода, освещения, конструкции деформационных швов, сопряжения моста с подходами.
Дорожная одежда:
многослойный плитный элемент, размещенный на плите пролетных строений в пределах проезжей (прохожей) части моста и обеспечивающий проектные профили поверхности проезда (прохода), защиту от воды, безопасность движения и передачу нагрузки от транспортных средств на плиту.
Примечание: дорожная одежда на плите проезжей части, содержит следующие слои:
- на железобетонной плите выравнивающий слой (при необходимости), гидроизоляцию, защитный слой и асфальтобетонное покрытие;
- на ортотропной плите, антикоррозионный, защитно-сцепляющий слои и асфальтобетонное покрытие (как правило).
Защитный слой бетона:
пласт бетона толщиной от наружной поверхности железобетонной конструкции до ближайшей поверхности арматуры, защищающий арматуру от коррозии.
Защитный слой гидроизоляции:
пласт бетона, укладываемый на гидроизоляцию для ее защиты от механических повреждений.
Выравнивающий слой:
пласт бетона, укладываемый на поверхность железобетонных плит проезжей части для выравнивания поверхности под гидроизоляцию.
Сборные конструкции:
железобетонные конструкции, изготавливаемые в виде отдельных элементов, транспортируемых и затем монтируемых на строительной площадке.
Монолитные конструкции:
железобетонные конструкции, формуемые на месте возведения.
Сборно-монолитные конструкции:
железобетонные конструкции, выполненные из сборных элементов и монолитного бетона.
Предварительно напряженные конструкции:
железобетонные конструкции, в которых на стадии изготовления или реконструкции создаются усилия обжатия, в том числе путем применения напрягаемой арматуры.
Анкер:
конструктивно-технологическое устройство для натяжения, фиксации и передачи усилия натяжения арматуры на бетон.
Арматура:
совокупность жестких (двутавры, швеллеры, уголки) и гибких (стержни, канаты, сетки, каркасы) элементов, устанавливаемых в железобетонные конструкции для восприятия преимущественно растягивающих напряжений, усиления бетона в сжатой зоне, а также создания предварительного напряжения конструкций.
Примечание: арматура подразделяется на рабочую (расчетную), монтажную и распределительную (конструктивную).
Система предварительного натяжения:
комплекс конструктивных элементов, в т.ч. армирования, устройств, а также оборудования для установки, натяжения, передачи и восприятия бетоном конструкции усилий обжатия от напрягаемых арматурных элементов.
Показатели конструктивных элементов
Строительный подъем:
выгиб вверх пролетного строения или его конструктивных элементов, компенсирующий прогиб от постоянной и части временной нагрузки, создаваемый в процессе изготовления или монтажа для обеспечения проектного очертания под эксплуатационными нагрузками.
Контролируемое усилие:
максимальное значение силы, прикладываемой к концам напрягаемой арматуры через натяжные устройства в процессе натяжения.
Дефект:
несоответствие конструктивного элемента установленным требованиям, образовавшееся до ввода сооружения в эксплуатацию.
Повреждение:
несоответствие конструктивного элемента установленным требованиям, образовавшееся после ввода моста в эксплуатацию.
Косвенное армирование:
арматурные элементы в виде размещенных перпендикулярно направлению сжимающего усилия сеток и/или спиралей, охватывающих напрягаемую арматуру, устанавливаемых в сжатых зонах конструкций для восприятия поперечных растягивающих усилий в этих зонах.
Термины, используемые в расчетах
Расчетная схема сооружения:
условное изображение конструктивных элементов, содержащее необходимые для расчета сооружения параметры, предназначенная для определения напряженно-деформированного состояния элементов.
Проектный (расчетный) срок службы:
установленный в строительных нормах или в задании на проектирование период использования конструктивного элемента или мостового сооружения в условиях его нормативного технического обслуживания до капитального ремонта и/или реконструкции и/или окончания эксплуатации, отсчитываемый с момента начала или возобновления эксплуатации объекта после капитального ремонта (реконструкции).
Нормативная характеристика:
максимальное значение параметра материала, фактора, воздействия, нагрузки, полученное по результатам испытаний с учетом статистических показателей установленной обеспеченности, как правило 0,95.
Сопротивление (напряжение):
показатель напряженного состояния материала, являющийся мерой интенсивности внутренних сил, отнесенной к единице площади и характеризующий степень противодействия внешним нагрузкам.
Временное сопротивление:
максимальное значение напряжения в материале для данного вида напряженного состояния, определенное в соответствие с требованиями стандартов.
Коэффициенты надежности (частные):
числовые множители, учитывающие возможные неблагоприятные отклонения значений нагрузок, характеристик материалов и расчетной схемы конструктивного элемента от реальных условий его эксплуатации, а также уровень ответственности мостового сооружения.
Временная нагрузка:
механические силы от транспортных средств, пешеходов и животных, а также силы природного происхождения, воздействующие на конструктивные элементы моста.
Характеристики конструкции и материала
Долговечность:
способность строительного объекта сохранять физические и другие свойства, устанавливаемые при проектировании и обеспечивающие его нормальную эксплуатацию в течение расчетного срока службы при надлежащем техническом обслуживании.
Трещиностойкость:
сопротивление железобетонных конструкций образованию и раскрытию трещин.
Усталость:
процесс накопления повреждений материала под действием переменных напряжений, приводящих к изменению свойств, образованию, развитию трещин и разрушению.
Ползучесть:
свойство материала увеличивать необратимую деформацию при постоянной нагрузке.
Релаксация напряжений:
процесс снижения напряжений от внешней нагрузки при постоянной величине деформации.
Сплошность бетона:
свойство, характеризующее непрерывность и однородность материала, в т.ч. характеризующуюся отсутствием аномальных зон, разуплотненного бетона, щебенистости и трещин.
Усадка бетона:
уменьшение объема, обусловленное процессом гидратации цемента и потерей воды затворения в процессе твердения бетона.
Класс бетона:
прочность бетона со статистической обеспеченностью 0,95.
Примечание: в зависимости от вида прочности бетона установлены классы бетона на: B - сжатие; B
t
- осевое растяжение; B
tb
- растяжение при изгибе.
Марка бетона по морозостойкости
F: буквенно-числовой идентификатор, обозначающий метод испытания бетона по стандартизированной методике и число циклов замораживания и оттаивания, которые бетон может выдержать без повреждений и снижения прочности, превышающих нормируемые показатели.
Призменная прочность бетона
- отношение разрушающей осевой сжимающей силы образца-призмы стандартных размеров к площади его сечения, нормального к этой силе.
[ГОСТ 24452-80]
Примечание: в тексте
СП 35.13330
термин "призменная прочность" используется для обозначения нормативной призменной прочности.
Модуль упругости:
коэффициент пропорциональности между нормальным напряжением и соответствующей ему относительной продольной упруго-мгновенной деформацией при осевом растяжении/сжатии образца.
Условные обозначения
R
bp
- расчетная прочность бетона на момент передачи напряжения с арматуры на бетон (передаточная прочность).
Все расчеты железобетонных элементов делятся на две большие группы: расчеты железобетонных элементов без предварительного напряжения и расчеты предварительно напряженных железобетонных элементов.
Все расчеты железобетонных элементов без предварительного напряжения делятся на три группы: расчеты изгибаемых элементов, расчеты внецентренно сжатых элементов и расчеты элементов, подверженных воздействию поперечных сил. Элементы подверженные воздействию поперечных сил могут быть как изгибаемыми элементами, так и внецентренно сжатыми
(рисунок 2.1)
.
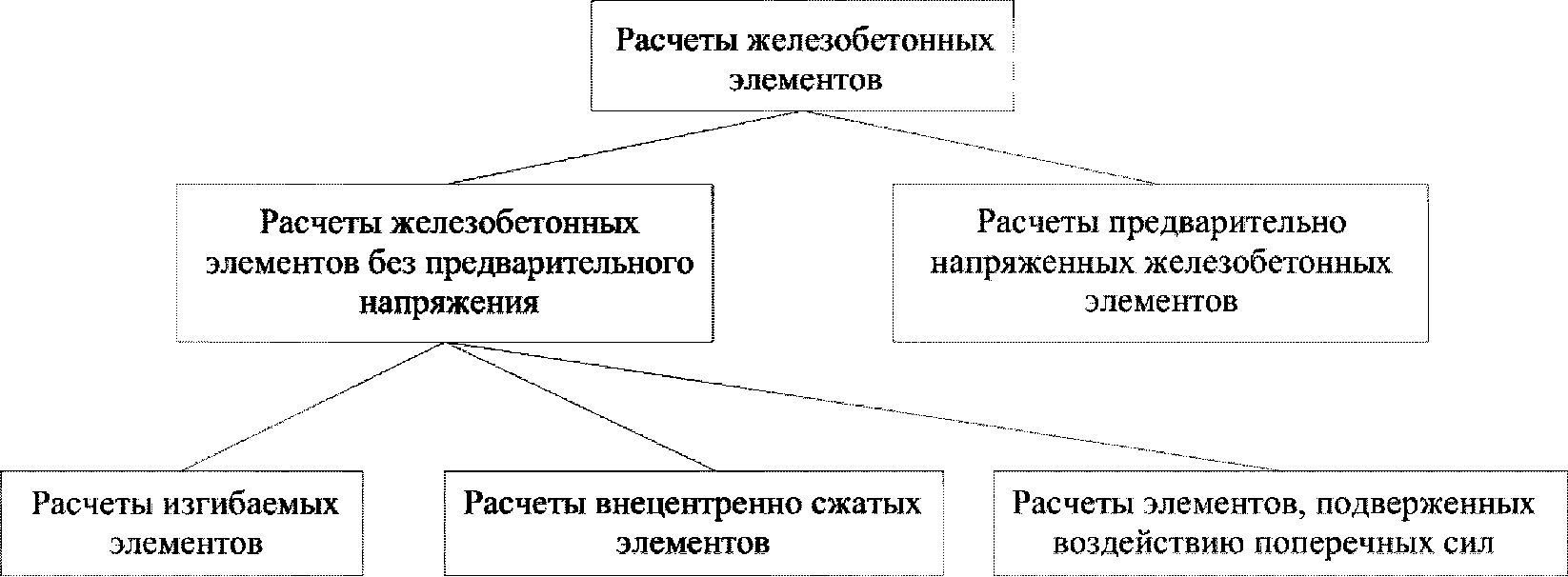
Изгибаемые элементы - это элементы, подверженные воздействию изгибающих моментов без воздействия продольных сил. Изгибаемые элементы также могут быть подвержены кручению и воздействию поперечных сил.
Внецентренно сжатые элементы - это элементы, подверженные воздействию сжимающих продольных сил, приложенных центрально или внецентренно. Внецентренно сжатые элементы могут быть также подвержены кручению и воздействию поперечных сил.
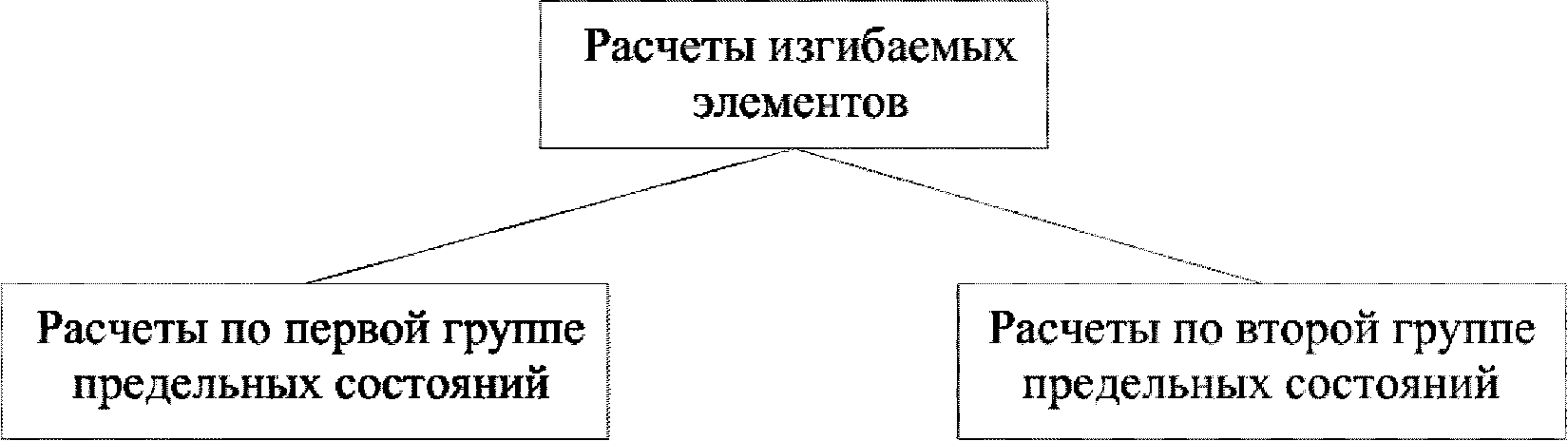
Расчеты изгибаемых элементов делятся на две большие группы: расчеты по первой группе предельных состояний и расчеты по второй группе предельных состояний
(рисунок 3.1)
.
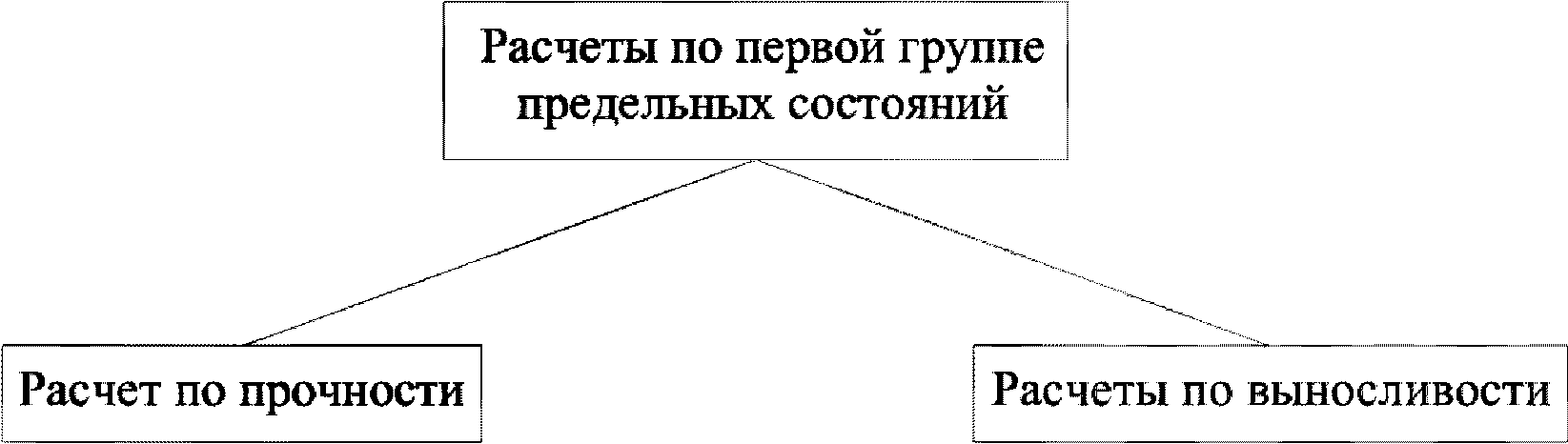
К расчетам изгибаемых элементов по первой группе предельных состояний относятся расчеты по прочности и выносливости
(рисунок 3.2)
.
Расчет изгибаемых элементов рекомендуется производить с использованием нелинейной деформационной модели и руководствуясь следующими предпосылками:
- сопротивление бетона растяжению принимается равным нулю;
- диаграммы деформирования бетона и арматуры двух- или трехлинейные;
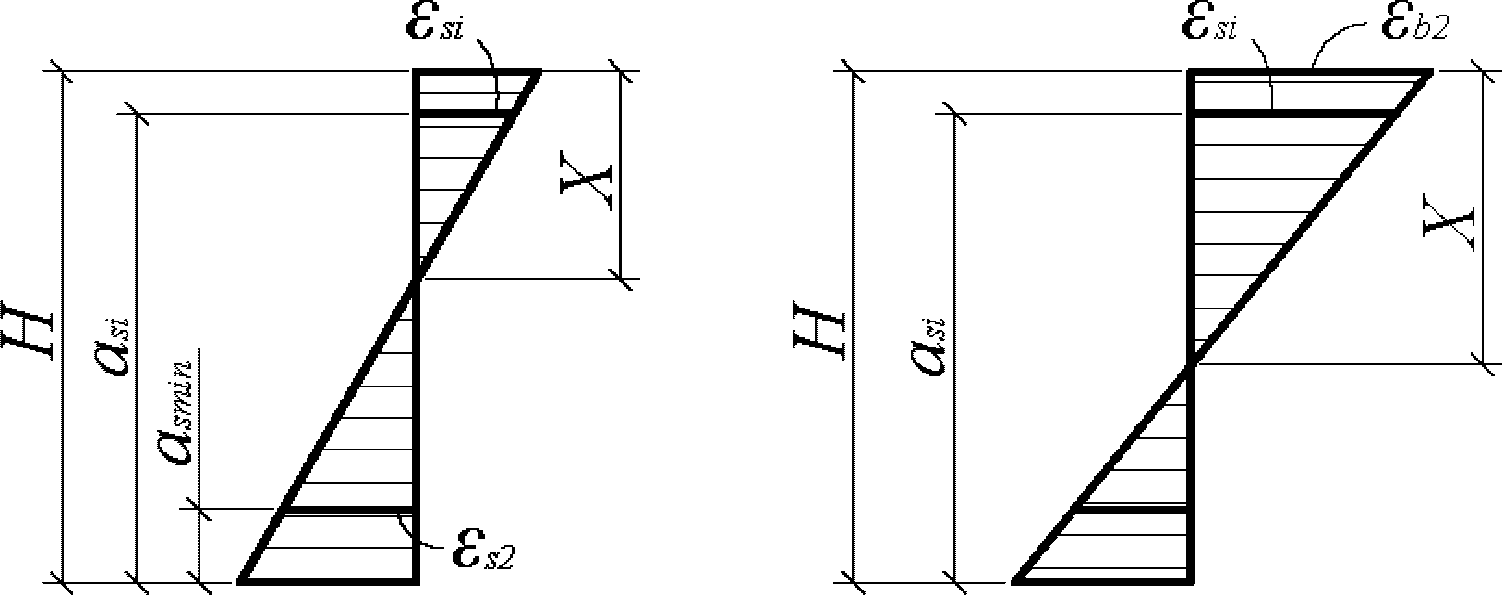
- эпюра относительных деформаций имеет линейный вид;
- для удобства расчетов принять верхнюю грань элемента наиболее сжатой, а нижнюю - наиболее растянутой.
При
M
I
> 0 верхняя грань сечения является наиболее сжатой и к расчету принимается нормально ориентированное сечение. При
M
I
< 0 нижняя грань сечения является наиболее сжатой и к расчету принимается обратное сечение (повернутое на 180°)
(рисунок 3.3)
;
M
I
-
момент от действия расчетных нагрузок, кНм.
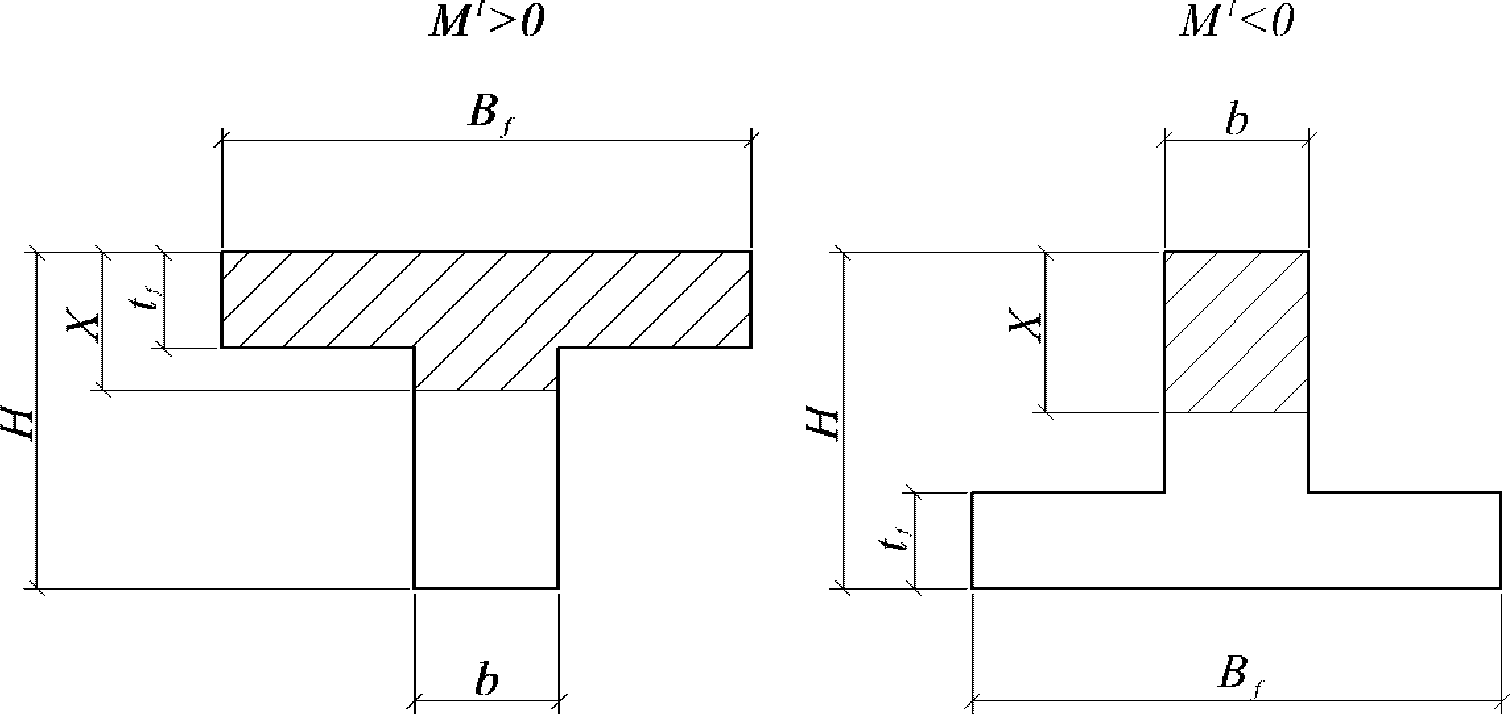
в зависимости от знака изгибающего момента
Предварительно сечение по высоте разбивается на элементарные участки с определенным шагом
 . Каждому участку присваивается порядковый номер - сверху вниз
(рисунок 3.4)
.
. Каждому участку присваивается порядковый номер - сверху вниз
(рисунок 3.4)
.
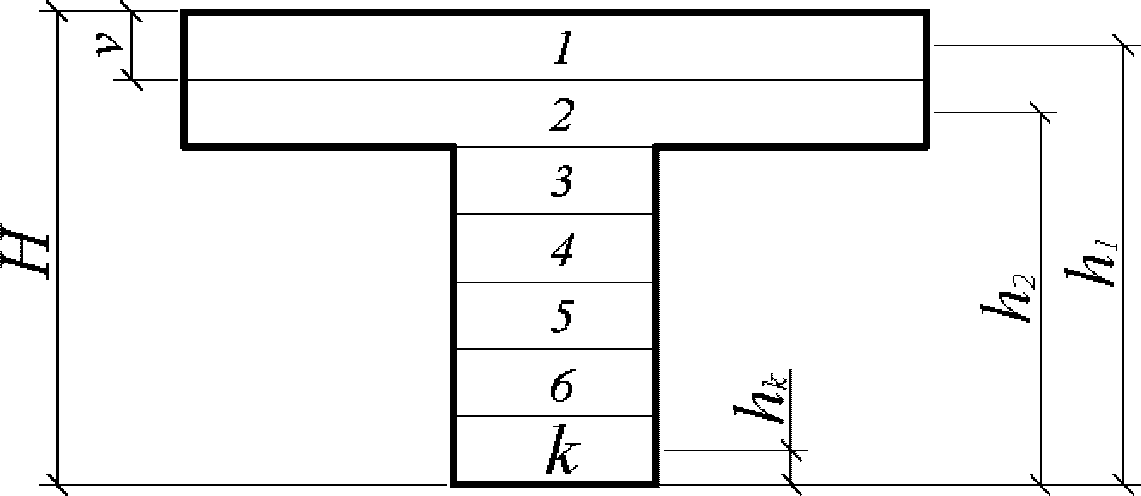
на элементарные участки
В общем случае расчет рекомендуется производить при помощи компьютерных средств путем подбора такой высоты сжатой зоны бетона
X
, при которой наблюдается равновесие системы:
где
k -
номер элементарного участка сечения;
l
- количество элементарных участков сечения;
N
bk
- усилие, возникающее в
k
-м элементарном участке, кН;
i
- номер ряда армирования;
m
- количество рядов армирования;
N
si
- усилие, возникающее в
i
-м ряду армирования, кН.
Возможны три варианта разрушения железобетонного сечения. Первый вариант предполагает разрушение сечения по растянутой арматуре, когда в одном из рядов армирования достигается предельная деформация растяжения арматуры
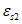 .
Второй вариант предполагает разрушение сечения по сжатому бетону, когда достигается предельная деформация сжатия бетона
.
Второй вариант предполагает разрушение сечения по сжатому бетону, когда достигается предельная деформация сжатия бетона
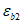 .
Третий вариант предполагает одновременное разрушение сечения по растянутой арматуре и сжатому бетону, когда предельная деформация растяжения арматуры
.
Третий вариант предполагает одновременное разрушение сечения по растянутой арматуре и сжатому бетону, когда предельная деформация растяжения арматуры
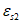 и предельная деформация сжатия бетона
и предельная деформация сжатия бетона
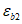 достигаются одновременно. Значение высоты сжатой зоны бетона
X
при третьем варианте развития событий называется граничной высотой сжатой зоны бетона
X
r
. Граничная высота сжатой зоны бетона
X
r
позволяет определить вариант разрушения сечения.
достигаются одновременно. Значение высоты сжатой зоны бетона
X
при третьем варианте развития событий называется граничной высотой сжатой зоны бетона
X
r
. Граничная высота сжатой зоны бетона
X
r
позволяет определить вариант разрушения сечения.
Граничная высота сжатой зоны бетона
X
r
определяется геометрически по эпюре относительных деформаций сечения
(рисунок 3.5)
:
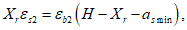 (3.3)
(3.3)
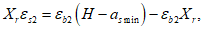 (3.4)
(3.4)
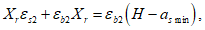 (3.5)
(3.5)
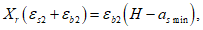 (3.6)
(3.6)
В
формулах (3.2)
-
(3.7)
:
H
- высота сечения
(рисунок 3.5)
, м;
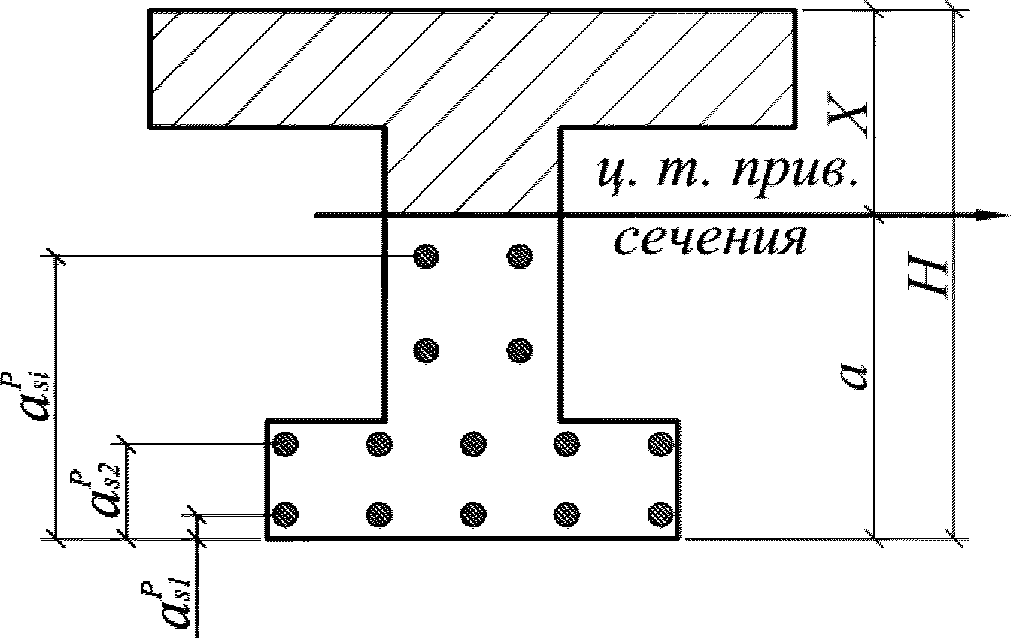
a
s
min
- расстояние между наиболее растянутой гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования
(рисунок 3.5)
, м;
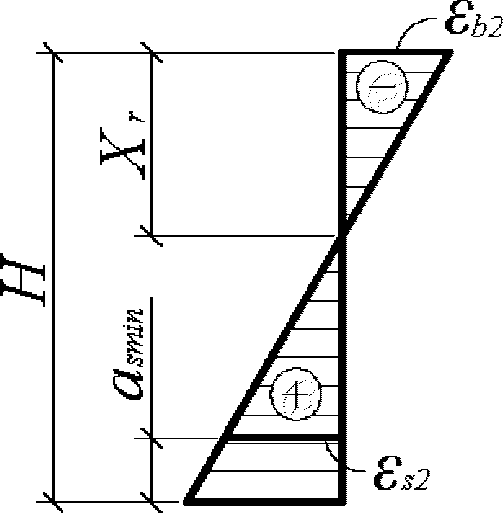
для расчета граничной высоты сжатой зоны бетона
Для удобства расчетов вводятся следующие условия:
при
X
<=
X
r
- первый вариант разрушения (разрушение по растянутой арматуре) или третий (одновременное разрушение сечения по арматуре и бетону);
при
X
>
X
r
- второй вариант разрушения (разрушение по сжатому бетону).
Усилия, возникающие в каждом элементарном участке
N
bk
, а также в каждом ряду армирования
N
si
, определяются по формулам:
В
формулах (3.8)
-
(3.9)
:
A
bk
- площадь
k
-го элементарного участка, м
2
;
A
si
- площадь
i
-го ряда армирования, м
2
;
Напряжения в элементарных участках бетонного сечения и рядах армирования определяются по диаграммам деформирования бетона и арматуры
(рисунок 3.6)
. Для упрощения расчетов допускается использовать двухлинейные диаграммы деформирования.
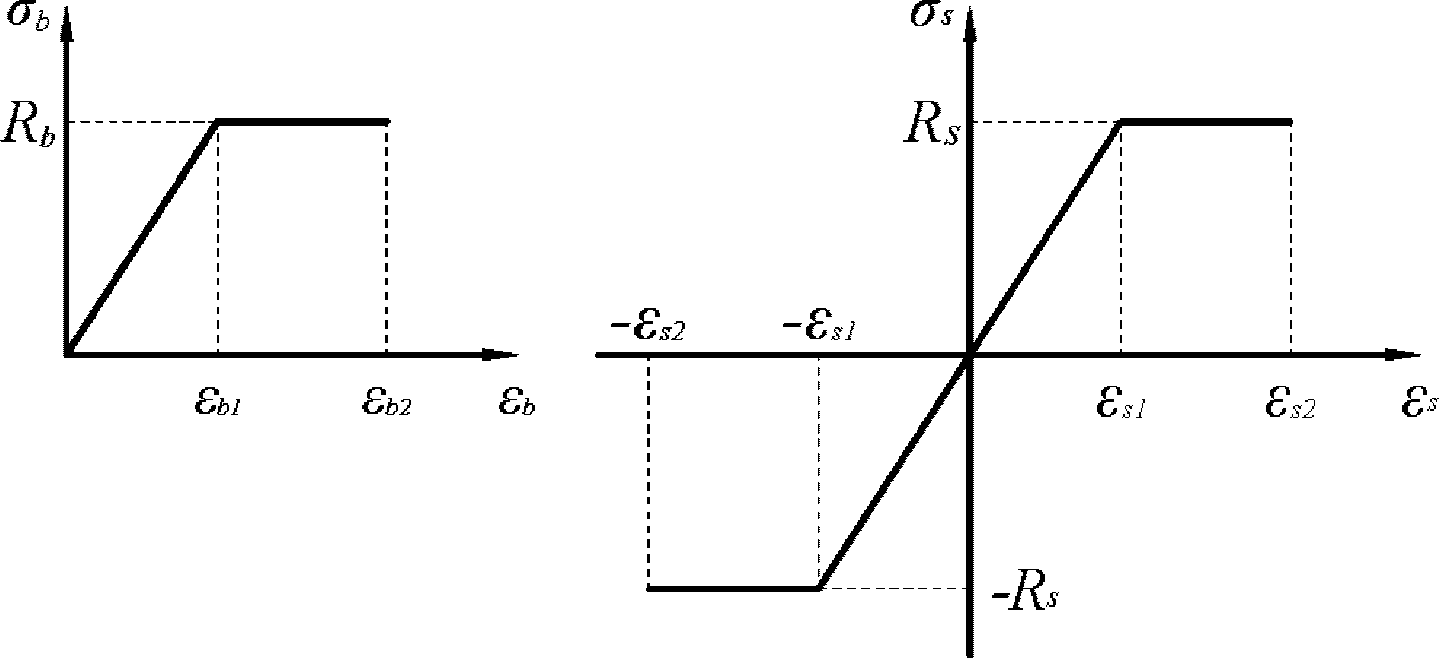
(слева) и арматуры (справа)
Для бетона двухлинейными диаграммами деформирования вводятся следующие условия:
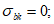 (3.11)
(3.11)
при
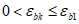 , (3.12)
, (3.12)
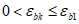 , (3.12)
, (3.12)
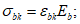 (3.13)
(3.13)
при
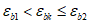 , (3.14)
, (3.14)
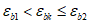 , (3.14)
, (3.14)
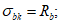 (3.15)
(3.15)
В
формулах (3.10)
-
(3.16)
:
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
Для арматуры двухлинейными диаграммами деформирования вводятся следующие условия:
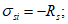 (3.18)
(3.18)
при
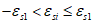 , (3.19)
, (3.19)
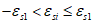 , (3.19)
, (3.19)
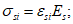 (3.20)
(3.20)
при
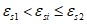 , (3.21)
, (3.21)
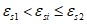 , (3.21)
, (3.21)
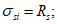 (3.22)
(3.22)
В
формулах (3.17)
-
(3.23)
:
R
s
- расчетное сопротивление арматуры согласно
таблице 7.16
СП 35.13330, кН/м
2
;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
Относительные деформации
k
-го элементарного участка бетонного сечения, определяются геометрически
(рисунок 3.7)
:
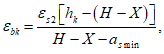 (3.25)
(3.25)
В
формулах (3.24)
-
(3.27)
:
h
k
- расстояние между нижней гранью сечения и центром
k
-го элементарного участка
(рисунок 3.7)
, м.
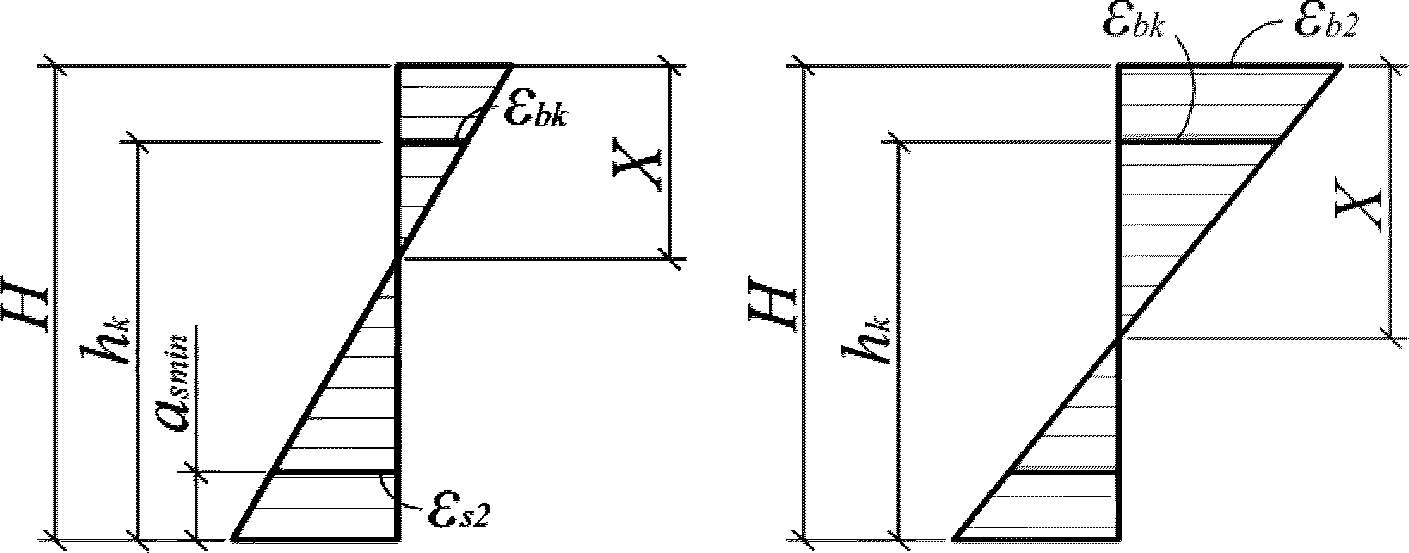
(слева - случай разрушения по арматуре, справа - по бетону)
Относительные деформации
i
-го ряда армирования, определяются геометрически
(рисунок 3.6)
:
при
X
>
X
r
, (3.30)
В
формулах (3.28)
-
(3.31)
:
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования
(рисунок 3.8)
, м.
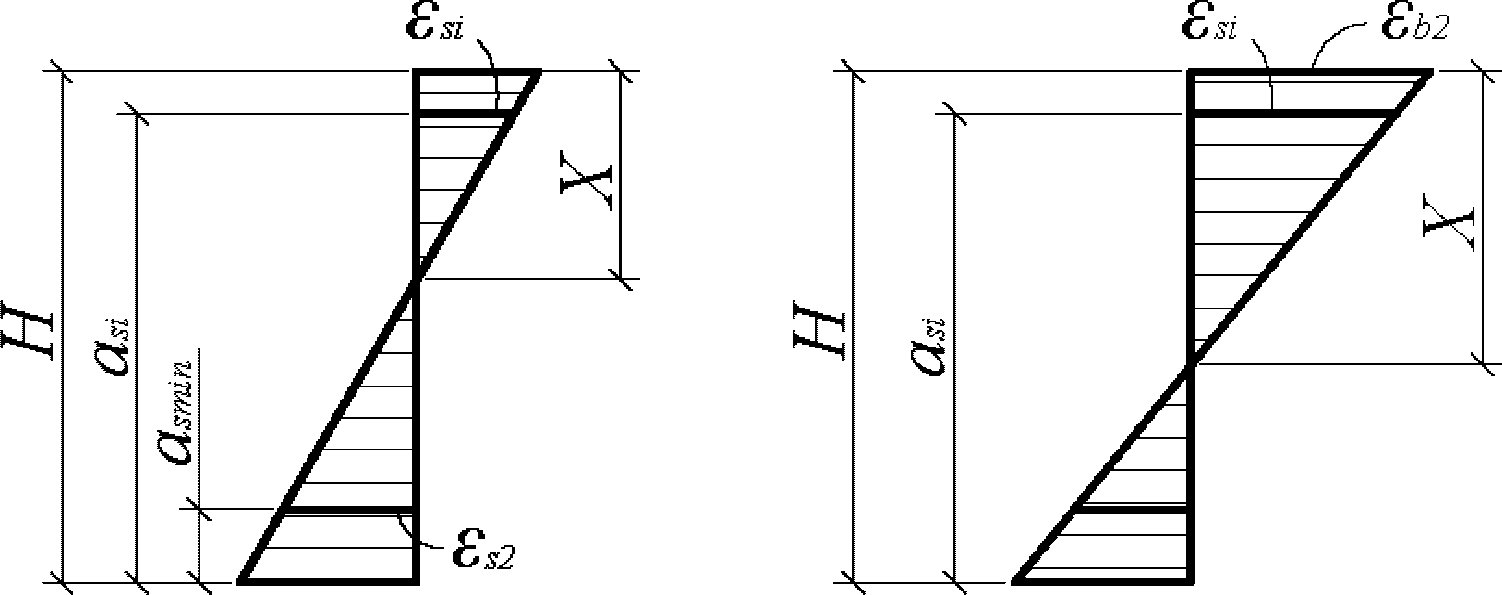
(слева - случай разрушения по арматуре, справа - по бетону)
Расстояние между нижней гранью сечения и центром
k
-го элементарного участка
h
k
бетонного сечения при нумерации участков сверху вниз от единицы и далее допускается определять по формуле:
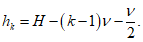 (3.32)
(3.32)
После определения высоты сжатой зоны бетона
X
, при которой соблюдается
условие (3.1)
, производится расчет предельного изгибающего усилия
M
ult
:
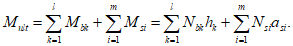 (3.33)
(3.33)
Расчет прочности сечения изгибаемого элемента заключается в проверке условия:
M
I
<=
M
ult
, (3.34)
где
M
I
- изгибающий момент от действия расчетных нагрузок, кНм.
Расчеты рекомендуется производить в табличном виде
(рисунок 3.9)
.
|
|
Параметры бетона
|
|||||||||
|
N
|
h
bk
|
A
bk
|
|
|
N
bk
|
M
bk
|
||||
|
п/п
|
м
|
м
2
|
-
|
кПа
|
кН
|
кНм
|
||||
|
|
|
1
|
|
|
|
|
|
|
||
|
|
|
2
|
|
|
|
|
|
|
||
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
||
|
|
|
5
|
|
|
|
|
|
|
||
|
|
|
6
|
|
|
|
|
|
|
||
|
|
|
k
|
|
|
|
|
|
|
||
|
|
|
|
||||||||
|
Параметры арматуры
|
||||||||
|
N
|
a
si
|
A
si
|
|
|
N
si
|
M
si
|
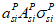
|
|
|
п/п
|
м
|
м
2
|
-
|
кПа
|
кН
|
кНм
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
i
|
|
|
|
|
|
|
|
|
|
|
|
|
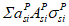
|
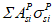
|
||||
Для расчета элементов, подверженных воздействию поперечных сил, необходимо определение положения равнодействующей усилий в растянутой арматуре.
Расстояние между нижней гранью сечения и равнодействующей усилий в растянутой арматуре
a
s
определяется по формуле:
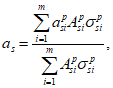 (3.35)
(3.35)
где
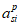 - расстояние между нижней гранью сечения и центром тяжести
i
-го растянутого ряда армирования, м;
- расстояние между нижней гранью сечения и центром тяжести
i
-го растянутого ряда армирования, м;
Для удобства расчетов вводится следующий критерий определения состояния арматуры:
при
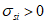 ,
,
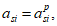 (3.36)
(3.36)
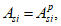 (3.37)
(3.37)
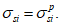 (3.38)
(3.38)
Перед расчетом по выносливости необходим расчет геометрических характеристик сечения
(рисунок 3.10)
.
┌───────────────────────┐
│Расчеты по выносливости│
└──────────┬────────────┘
┌────────────────────┴──────────────────────┐
│Расчет геометрических характеристик сечения│
└────────────────────┬──────────────────────┘
┌──────────┴───────────┐
│Расчет по выносливости│
└──────────────────────┘
Перед расчетом по выносливости необходимо получить усилия от двух загружений, одно из которых предполагает достижение максимальных нормальных напряжений в бетоне и арматуре, а второе - минимальных. Также необходимо определиться с типом нагрузок (знакопостоянные или знакопеременные), воздействующих на элемент.
Знакопостоянными нагрузками называются такие нагрузки первого и второго загружений, которые вызывают сжатие и растяжение одних и тех же граней сечения
(рисунок 3.11)
.
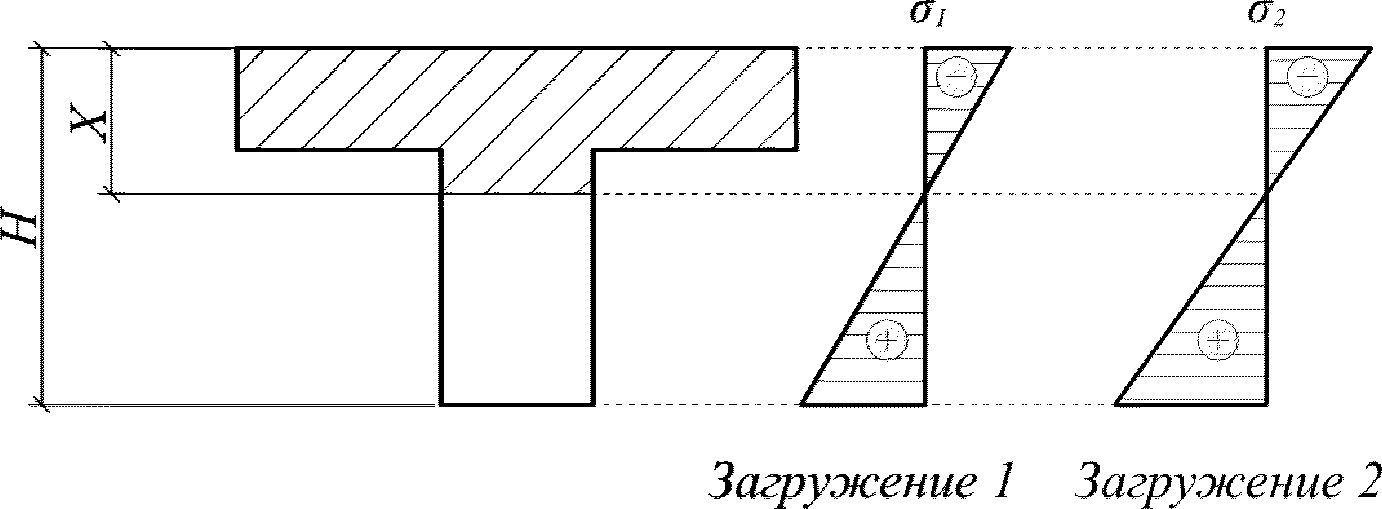
от знакопостоянных нагрузок
Знакопеременными нагрузками называются такие нагрузки первого и второго загружений, которые вызывают сжатие и растяжение разных граней сечения
(рисунок 3.12)
.

от знакопеременных нагрузок
Перед началом расчета необходимо определиться являются ли нагрузки от первого и второго загружений знакопеременными или знакопостоянными:
при
 и
и
 - знакопостоянные;
- знакопостоянные;
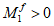 и
и
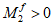 - знакопостоянные;
- знакопостоянные;
при
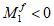 и
и
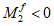 - знакопостоянные;
- знакопостоянные;
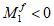 и
и
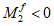 - знакопостоянные;
- знакопостоянные;
при
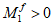 и
и
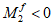 - знакопеременные;
- знакопеременные;
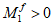 и
и
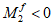 - знакопеременные;
- знакопеременные;
при
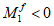 и
и
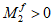 - знакопеременные.
- знакопеременные.
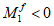 и
и
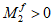 - знакопеременные.
- знакопеременные.
Если нагрузки являются знакопеременными, то перед расчетом по выносливости необходим расчет геометрических характеристик нормально ориентированного сечения и обратного сечения (повернутого на 180°). Если нагрузки являются знакопостоянными, то производится расчет геометрических характеристик нормально ориентированного сечения
(рисунок 3.13)
.
характеристик нормально ориентированного
сечения (справа) и обратного (слева)
Геометрические характеристики определяются без учета работы бетона растянутой зоны.
Для удобства расчетов верхняя грань элемента принимается наиболее сжатой, а нижняя - наиболее растянутой
(рисунок 3.14)
.
характеристик приведенного сечения
Общий случай расчета предполагает подбор такой высоты сжатой зоны бетона
X
, при которой статический момент инерции приведенного сечения относительно его же центра тяжести обращается в ноль:
S
B
-
S
H
= 0, (3.39)
где
S
B
- статический момент инерции сжатой части сечения, лежащей выше центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения, м
3
;
S
H
- статический момент инерции растянутой части сечения, лежащей ниже центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения, м
3
.
Статический момент инерции сжатой части сечения, лежащей выше центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения
S
B
, определяется по формуле:
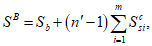 (3.40)
(3.40)
где
S
b
- статический момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, м
3
;
i
- номер ряда армирования;
m
- количество рядов армирования;
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330.
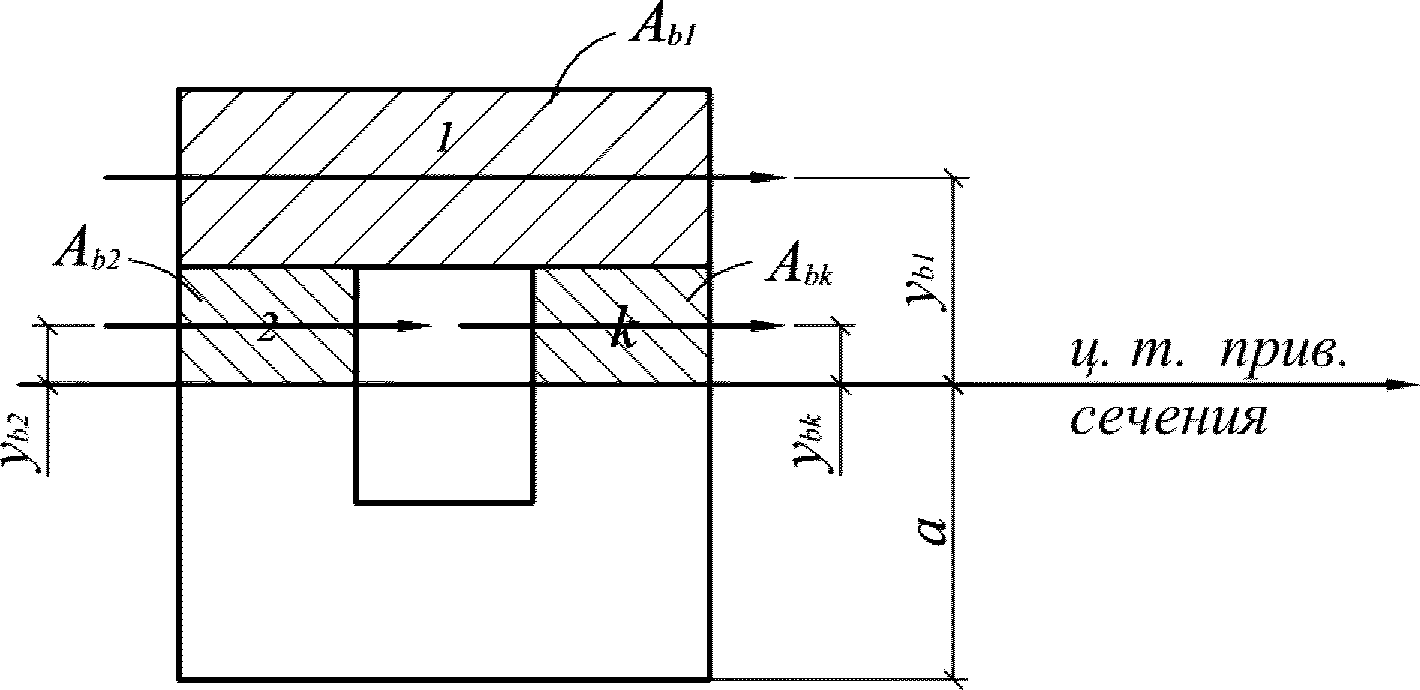
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. Статический момент инерции сжатой бетонной части
S
b
, разбитой на отдельные участки, определяется по формуле:
где
k
- номер участка сечения;
l
- количество участков сечения;
S
bk
- статический момент инерции
k
-го участка сечения, взятый относительно центра тяжести приведенного сечения, м
3
;
A
bk
- площадь
k
-го участка сечения
(рисунок 3.15)
, м
2
;
y
bk
- расстояние между центром тяжести
k
-го участка и центром тяжести приведенного сечения
(рисунок 3.15)
, м.
Статический момент инерции
i
-го сжатого ряда армирования
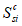 определяется по формуле:
определяется по формуле:
В
формулах (3.42)
-
(3.43)
:
a
- высота растянутой зоны бетона
(рисунок 3.16)
, м;
H
- высота сечения
(рисунок 3.16)
, м.
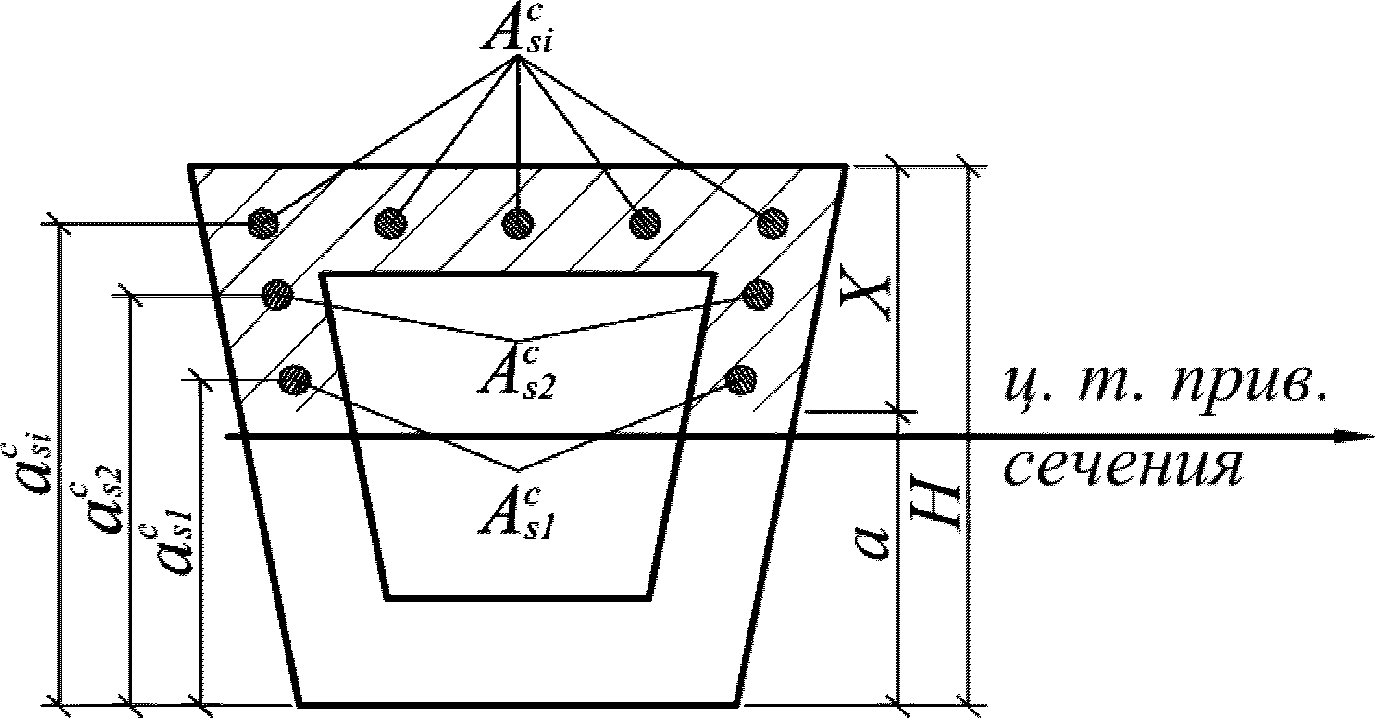
Статический момент инерции растянутой части сечения, лежащей ниже центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения
S
H
, определяется по формуле:
В
формулах (3.44)
-
(3.45)
:
Для удобства расчетов вводятся следующие критерии определения состояния арматуры:
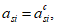 (3.47)
(3.47)
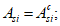 (3.48)
(3.48)
при
a
si
<
a
, (3.49)
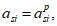 (3.50)
(3.50)
В
формулах (3.46)
-
(3.51)
:
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м;
A
si
- площадь
i
-го ряда армирования, м
2
.
Приведенные выше формулы позволяют вычислить высоту сжатой зоны бетона
X.
Момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения
I
red
, определяется по формуле:
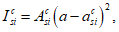 (3.53)
(3.53)
В
формулах (3.52)
-
(3.54)
:
I
b
- момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, м
4
;
Момент инерции сжатой бетонной части сечения
I
b
, разбитой на отдельные участки, определяется по формуле:
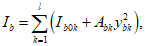 (3.55)
(3.55)
где
I
b
0
k
- собственный момент инерции
k
-го участка сечения.
Напряжения в бетоне и арматуре определяются по правилам расчета упругих материалов.
Расчет нормальных напряжений в бетоне и арматуре при знакопостоянных нагрузках производится по формулам:
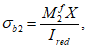 (3.57)
(3.57)
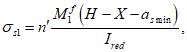 (3.58)
(3.58)
В
формулах (3.56)
-
(3.59)
:
X
- высота сжатой зоны бетона нормально ориентированного сечения
(рисунок 3.18)
, м;
I
red
- момент инерции нормально ориентированного приведенного сечения, взятый относительно центра тяжести нормально ориентированного приведенного сечения, м
4
;
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330;
a
s
min
- расстояние между наиболее растянутой гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования
(рисунок 3.18)
, м.
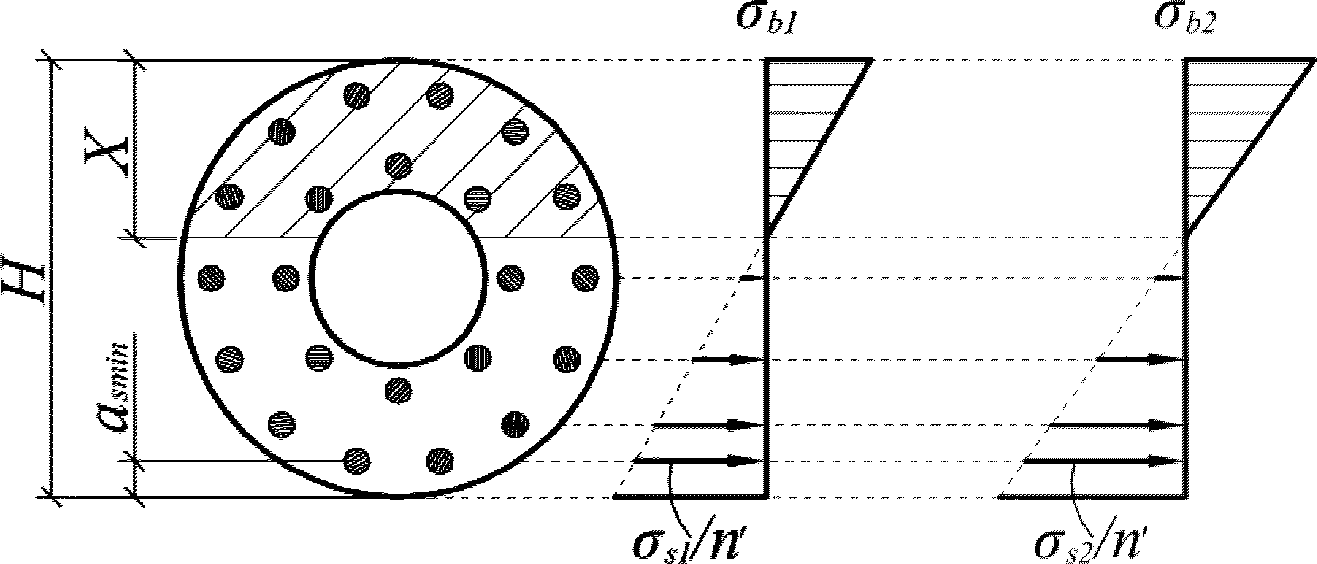
от знакопостоянных нагрузок
Расчет коэффициентов асимметрии цикла для бетона
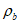 и арматуры
и арматуры
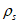 при знакопостоянных нагрузках производится по формулам:
при знакопостоянных нагрузках производится по формулам:
В
формулах (3.57)
-
(3.58)
:
Расчетные сопротивления бетона сжатию
R
bf
и арматурной стали растяжению
R
sf
при расчетах по выносливости при знакопостоянных нагрузках определяются по формулам:
В
формулах (3.59)
-
(3.60)
:
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
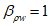 );
);
R
s
- расчетное сопротивление арматуры растяжению согласно
таблице 7.16
СП 35.13330, кН/м
2
.
Расчет изгибаемых элементов по выносливости заключается в ограничении максимальных нормальных сжимающих напряжений в бетоне
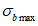 и максимальных нормальных растягивающих напряжений в арматуре
и максимальных нормальных растягивающих напряжений в арматуре
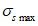 . Ограничения напряжений при знакопостоянных нагрузках производятся исходя из условий:
. Ограничения напряжений при знакопостоянных нагрузках производятся исходя из условий:
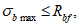 (3.61)
(3.61)
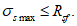 (3.62)
(3.62)
При расчетах на знакопеременные нагрузки вводится дополнительное допущение. Принимается, что нагрузки вызывающие сжатие верхней грани сечения, относятся к первому загружению, а нагрузки, вызывающие сжатие нижней грани сечения, относятся ко второму загружению.
Расчет нормальных напряжений в бетоне и арматуре при знакопеременных нагрузках производится по формулам:
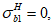 (3.64)
(3.64)
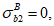 (3.65)
(3.65)
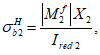 (3.66)
(3.66)
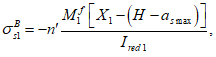 (3.67)
(3.67)
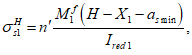 (3.68)
(3.68)
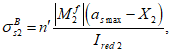 (3.69)
(3.69)
В
формулах (3.63)
-
(3.70)
:
X
1
- высота сжатой зоны бетона нормально ориентированного сечения
(рисунок 3.19)
, м;
I
red
1
- момент инерции нормально ориентированного приведенного сечения, взятый относительно центра тяжести нормально ориентированного приведенного сечения, м
4
;
X
2
- высота сжатой зоны бетона обратного сечения
(рисунок 3.19)
, м;
I
red
2
- момент инерции обратного приведенного сечения, взятый относительно центра тяжести обратного приведенного сечения, м
4
;
a
s
max
- расстояние между нижней гранью сечения и центром тяжести наиболее удаленного от нее ряда армирования
(рисунок 3.19)
, м;
a
s
min
- расстояние между нижней гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования;
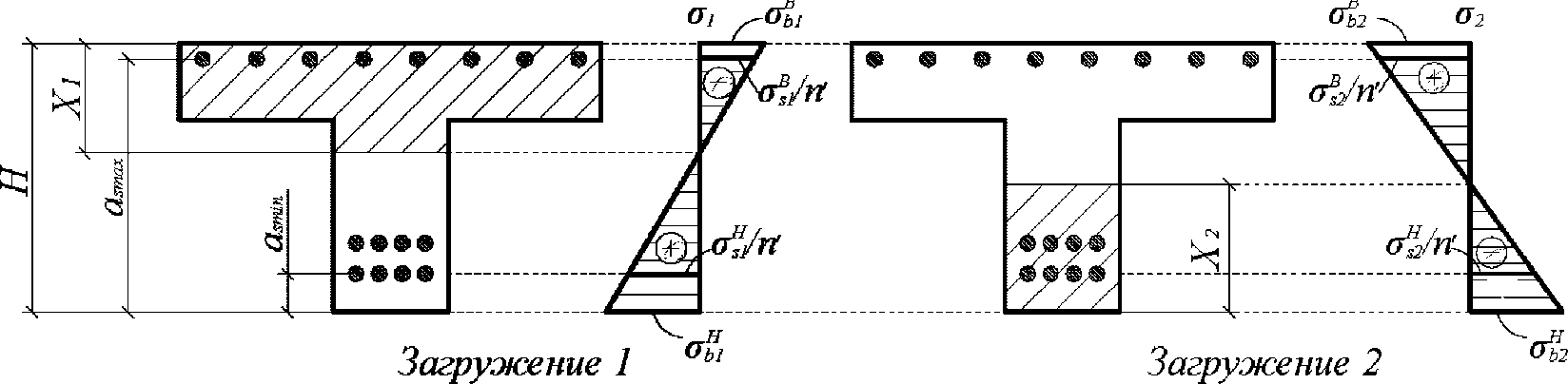
от знакопеременных нагрузок
Расчет коэффициентов асимметрии цикла для бетона и арматуры при знакопеременных нагрузках производится по формулам:
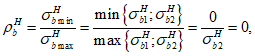 (3.72)
(3.72)
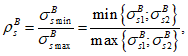 (3.73)
(3.73)
В
формулах (3.71)
-
(3.74)
:
Расчетные сопротивления бетона сжатию
R
bf
и арматурной стали растяжению при расчетах по выносливости при знакопеременных нагрузках определяются по формулам:
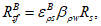 (3.76)
(3.76)
В
формулах (3.75)
-
(3.77)
:
Расчет изгибаемых элементов по выносливости заключается в ограничении максимальных нормальных сжимающих напряжений в бетоне
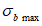 и максимальных нормальных растягивающих напряжений в арматуре. Ограничение напряжений при знакопеременных нагрузках производится исходя из условий:
и максимальных нормальных растягивающих напряжений в арматуре. Ограничение напряжений при знакопеременных нагрузках производится исходя из условий:
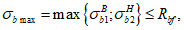 (3.78)
(3.78)
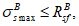 (3.79)
(3.79)
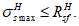 (3.80)
(3.80)
Выше представленный подход к расчету по выносливости на знакопеременную нагрузку обоснован тем, что заранее сложно предугадать какая грань сечения определяет выносливость элемента по бетону и какой ряд армирования определяет выносливость элемента по арматуре.
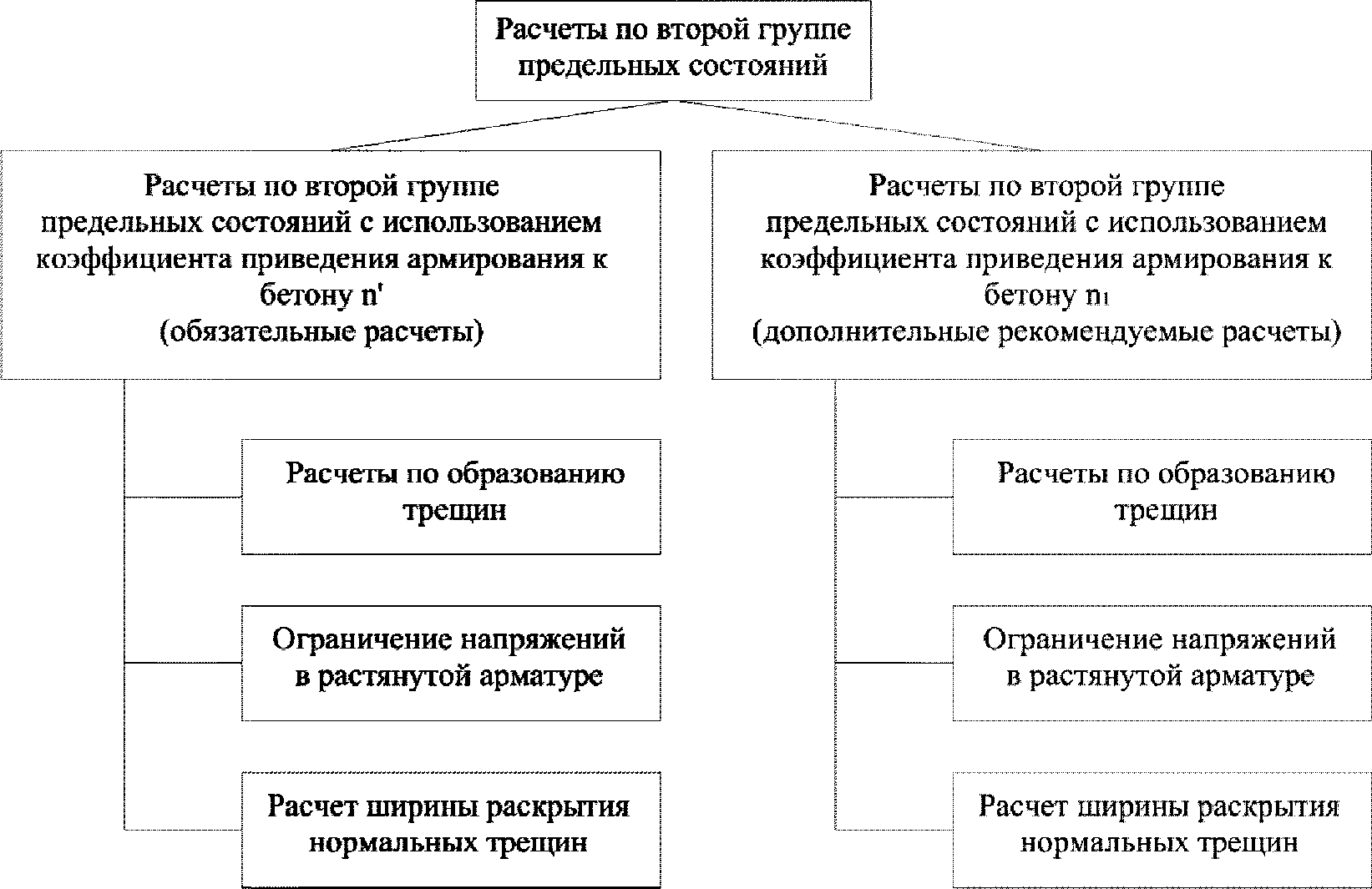
К расчетам по второй группе предельных состояний относятся расчеты по образованию трещин, расчет по ограничению напряжений в растянутой арматуре и расчет ширины раскрытия нормальных трещин
(рисунок 3.20)
.
Согласно требованиям
п. 7.48
СП 35.13330 для расчетов на трещиностойкость (для расчета напряжений и геометрических характеристик) используется коэффициент приведения армирования к бетону, учитывающий влияние виброползучести бетона
n'
.
Виброползучесть бетона - это длительный процесс, а усилия, на которые производится расчет по второй группе предельных состояний, возникают и на ранних стадиях эксплуатации конструкции. Поэтому авторы данного пособия также рекомендуют производить все проверки по второй группе предельных состояний с расчетом напряжений и геометрических характеристик сечения при коэффициенте приведения армирования к бетону
n
1
:
В
формулах (3.81)
-
(3.82)
:
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
.
Расчет по образованию трещин заключается в ограничении нормальных сжимающих напряжений в бетоне. Для расчета напряжений предварительно необходимо вычислить геометрические характеристики сечения. Геометрические характеристики сечения определяются без учета работы бетона растянутой зоны
(рисунок 3.21)
.
┌─────────────────────────────┐
│Расчеты по образованию трещин│
└─────────────┬───────────────┘
┌────────────────────┴──────────────────────┐
│Расчет геометрических характеристик сечения│
└────────────────────┬──────────────────────┘
┌─────────────┴───────────────┐
│Расчет по образованию трещин │
└─────────────────────────────┘
Расчет геометрических характеристик сечения при расчетах по второй группе предельных состояний производится согласно
3.1.2.1
, но с заменой коэффициента приведения армирования к бетону
n'
на
n.
Коэффициент приведения армирования к бетону
n
определяется согласно
3.2.1
.
Нормальные сжимающие напряжения в бетоне
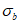 определяются по формуле:
определяются по формуле:
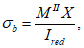 (3.83)
(3.83)
где
M
II
- изгибающий момент от действия нормативных нагрузок, кНм;
X
- высота сжатой зоны бетона согласно
3.2.1.1
(рисунок 3.22)
, м;
I
red
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, согласно
3.2.1.1
, м
4
.
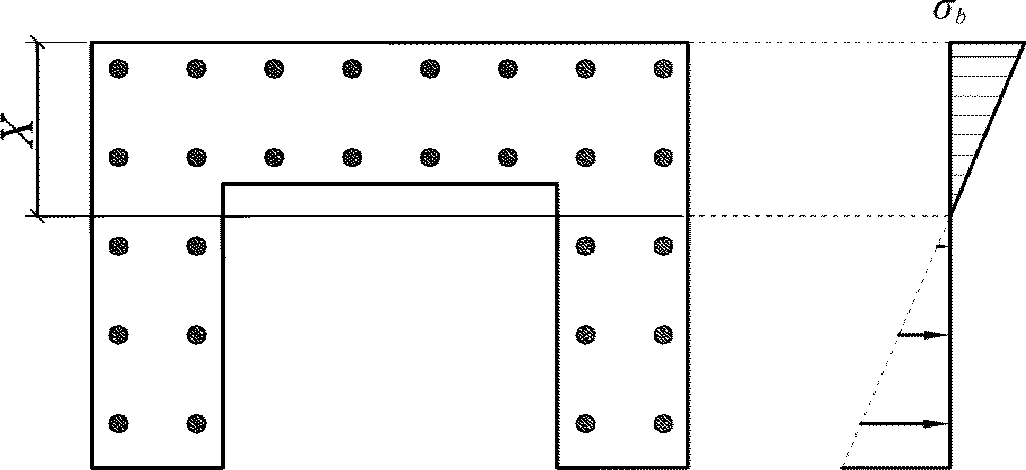
сжимающих напряжений в бетоне
Ограничение нормальных сжимающих напряжений в бетоне
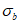 производится согласно условию:
производится согласно условию:
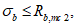 (3.84)
(3.84)
где
R
b,mc
2
- сопротивление бетона осевому сжатию для расчетов по предотвращению образования в конструкциях продольных трещин на стадии эксплуатации согласно
таблице 7.6
СП 35.13330, кН/м
2
.
Нормальные напряжения в наиболее растянутом ряду армирования
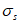 определяются по формуле:
определяются по формуле:
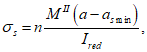 (3.85)
(3.85)
где
n
- коэффициент приведения армирования к бетону согласно
3.2.1
;
M
II
- изгибающий момент от действия нормативных нагрузок, кНм;
a
- высота растянутой зоны бетона, согласно
3.2.1.1
(рисунок 3.23)
, м;
a
s
min
- расстояние между наиболее растянутой гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования
(рисунок 3.23)
, м;
I
red
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, согласно
3.2.1.1
, м
4
.
в растянутой арматуре
Ограничение нормальных напряжений в наиболее растянутом ряду армирования
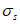 производится согласно условию:
производится согласно условию:
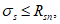 (3.86)
(3.86)
где
R
sn
- нормативное сопротивление арматуры растяжению согласно
таблицам 7.15
и
7.16
СП 35.13330, кН/м
2
.
Расчет заключается в определении ширины раскрытия нормальных трещин
a
cr
и сравнении ее с предельным значением расчетной ширины раскрытия трещин
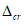 .
.
Расчетная ширина раскрытия нормальных трещин
a
cr
определяется по формуле:
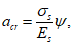 (3.87)
(3.87)
где
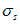 - напряжения в наиболее растянутом ряду армирования согласно
3.2.2
, кН/м
2
;
- напряжения в наиболее растянутом ряду армирования согласно
3.2.2
, кН/м
2
;
E
s
- модуль упругости армирования, кН/м
2
;
Ограничение ширины раскрытия нормальных трещин производится согласно условию:
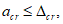 (3.88)
(3.88)
где
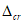 - предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
- предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
Для гладкой стержневой арматуры, арматурных пучков из гладкой проволоки и для стальных закрытых канатов коэффициент раскрытия трещин
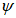 определяется по формуле:
определяется по формуле:
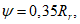 (3.89)
(3.89)
где
R
r
- радиус армирования, см.
Для стержневой арматуры периодического профиля, проволок периодического профиля класса Вр, пучков из этой проволоки, канатов класса К7 и пучков из них, стальных канатов со спиральной и двойной свивкой, а также для любой арматуры в стенках коэффициента раскрытия трещин
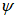 определяется по формуле:
определяется по формуле:
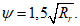 (3.90)
(3.90)
Радиус армирования
R
r
определяется по формуле:
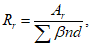 (3.91)
(3.91)
где
A
r
- площадь зоны взаимодействия для нормального сечения, принимаемая ограниченной наружным контуром сечения и радиусом взаимодействия
r
, которая не должна выходить за пределы растянутой зоны сечения
(рисунок 3.24)
, см
2
;
n
- число арматурных элементов с одинаковым номинальным диаметром
d
;
d
- диаметр одного стержня (включая случаи расположения в группах), см.
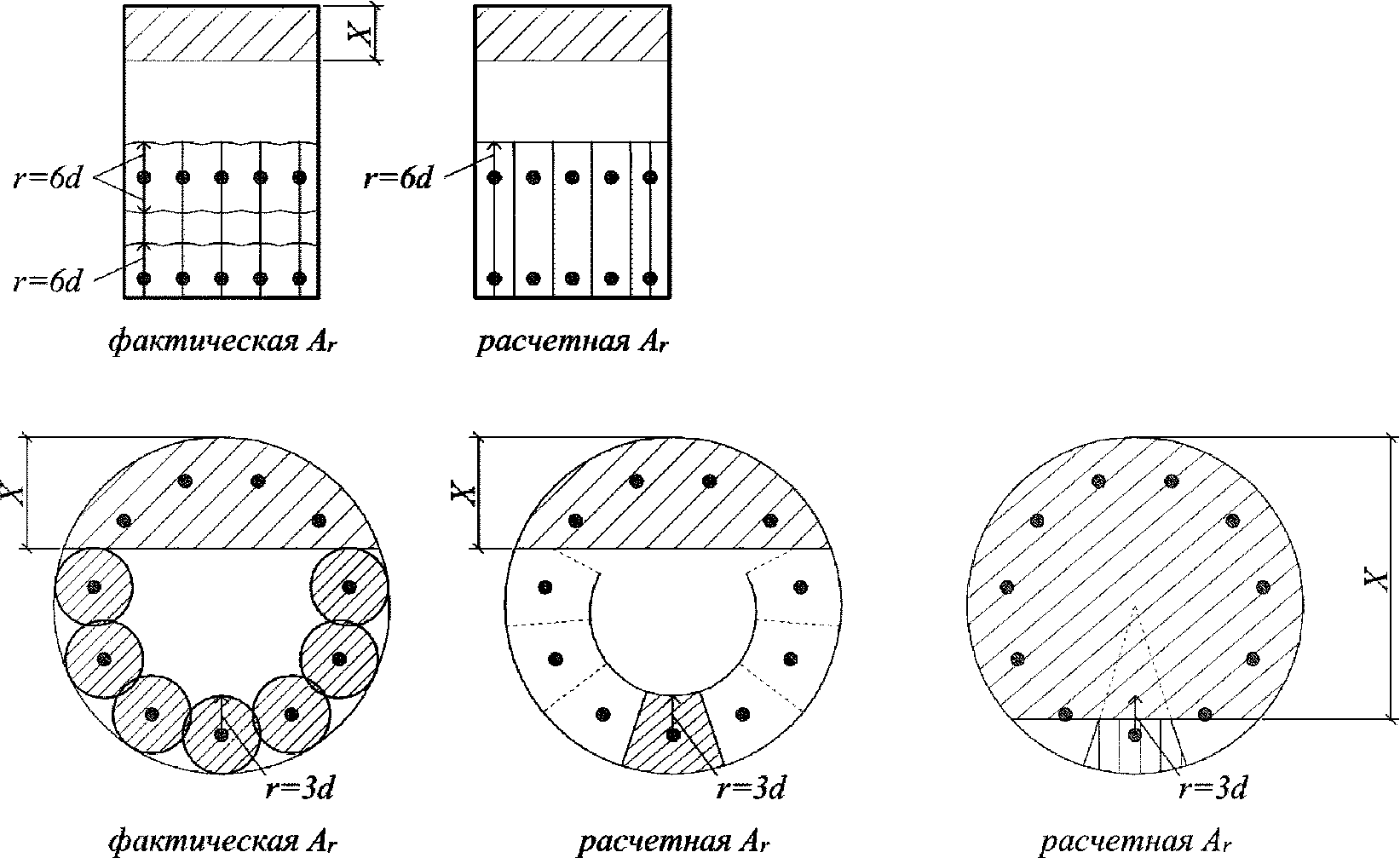
В круглых сечениях площадь зоны взаимодействия
A
r
и радиус армирования
R
r
следует определять для наиболее растянутого стержня или пучка.
Высота растянутой зоны сечения
a
определяется согласно
3.2.1.1
.
Для непрямоугольных сечений с арматурой, равномерно распределенной по контуру, радиус взаимодействия принимается
r
= 3
d.
Для пучков и канатов диаметр
d
соответствует наружному контуру арматурного элемента, а
r =
5
d.
Во всех остальных случаях
r =
6
d.
Сумма
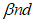 определяется по формуле:
определяется по формуле:
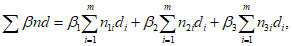 (3.92)
(3.92)
где
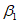 - коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
- коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
n
1
i
- количество одиночных стержней в
i
-ом ряду армирования;
d
i
- диаметр стержней
i
-го ряда армирования, см;
n
2
i
- количество сдвоенных стержней в
i
-ом ряду армирования;
n
3
i
- количество строенных стержней в
i
-ом ряду армирования.
Внецентренно сжатые элементы должны быть рассчитаны в соответствии с методикой представленной в этой главе как в плоскости изгиба, так и из плоскости изгиба. Расчеты делятся на две большие группы: расчеты по первой группе предельных состояний и расчеты по второй группе предельных состояний
(рисунок 4.1)
.
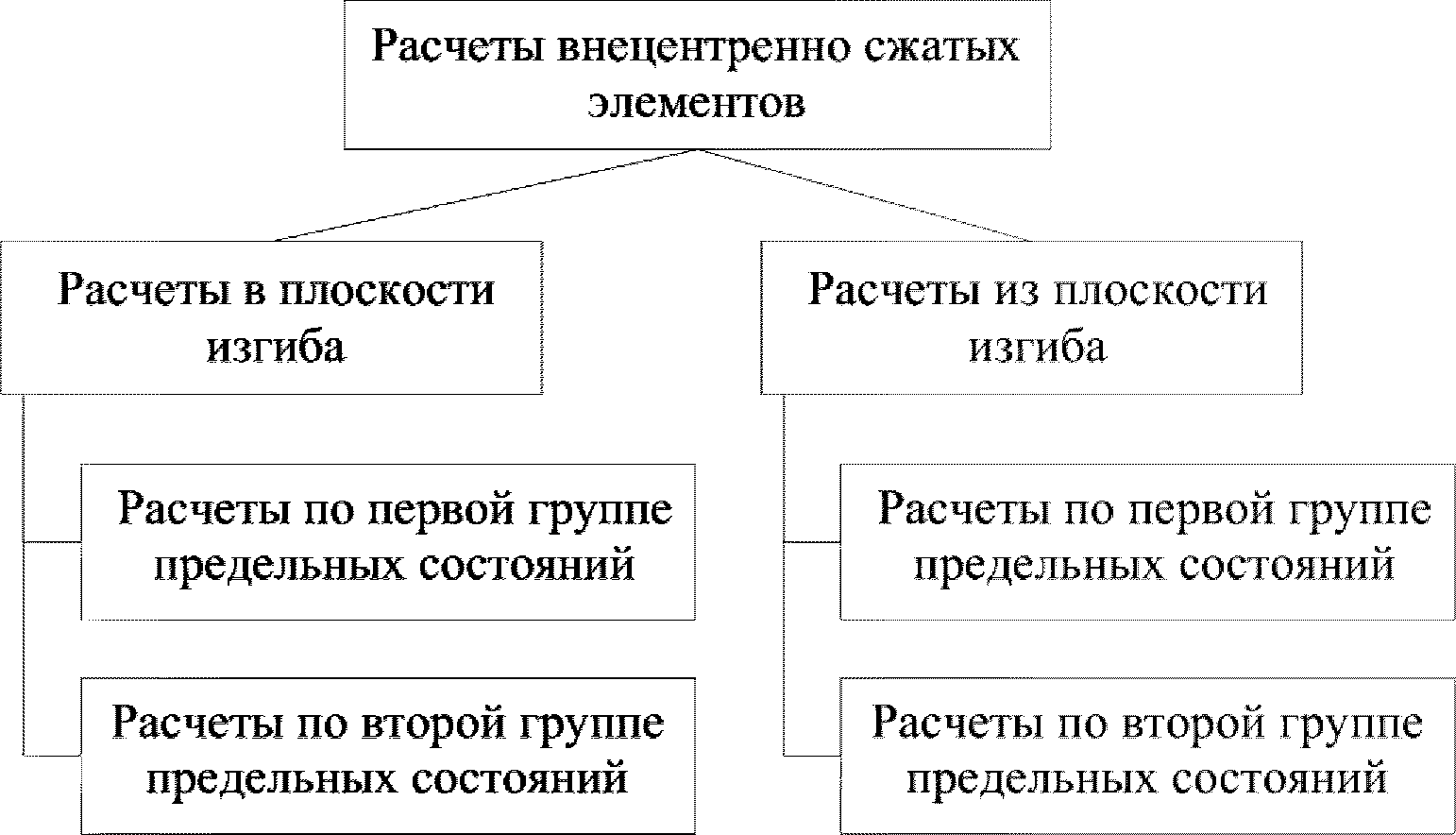
К расчетам внецентренно сжатых элементов по первой группе предельных состояний относятся расчеты по прочности, устойчивости, выносливости и расчет по ограничению сжимающих усилий
(рисунок 4.2)
.
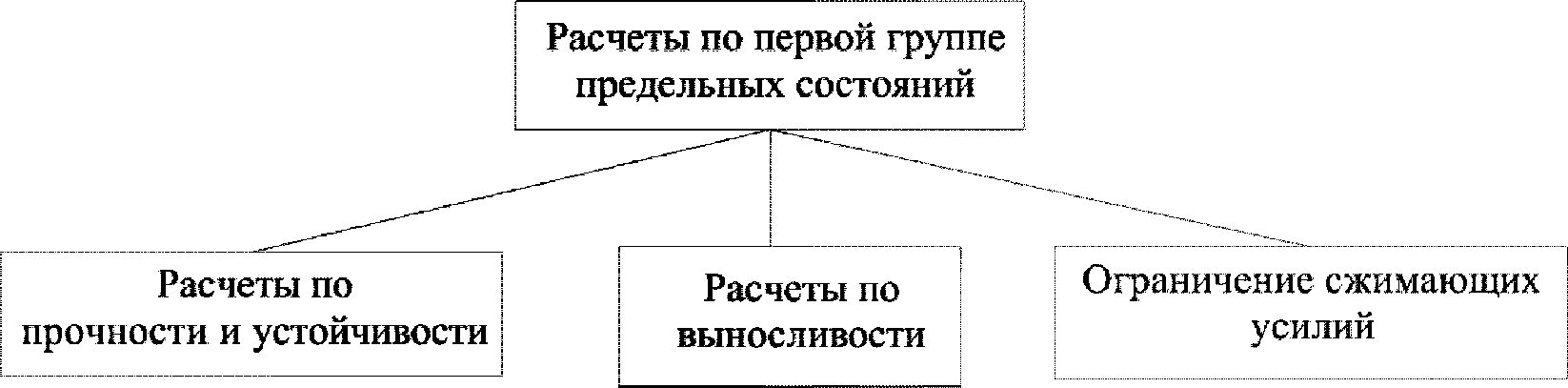
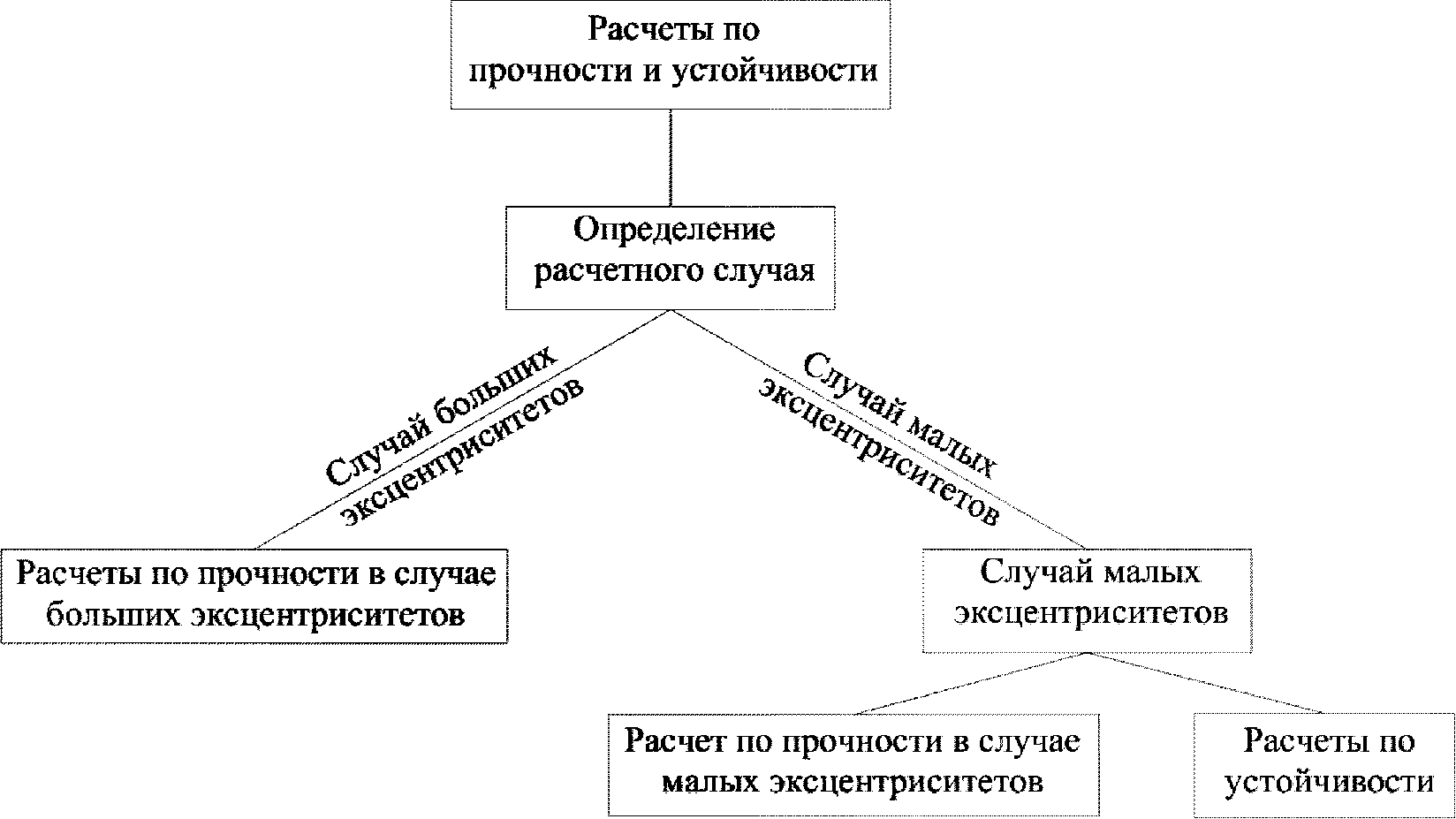
В зависимости от величины эксцентриситета приложения сжимающей силы производятся расчеты по прочности в случае больших эксцентриситетов или расчеты по прочности в случае малых эксцентриситетов и расчеты по устойчивости
(рисунок 4.3)
.
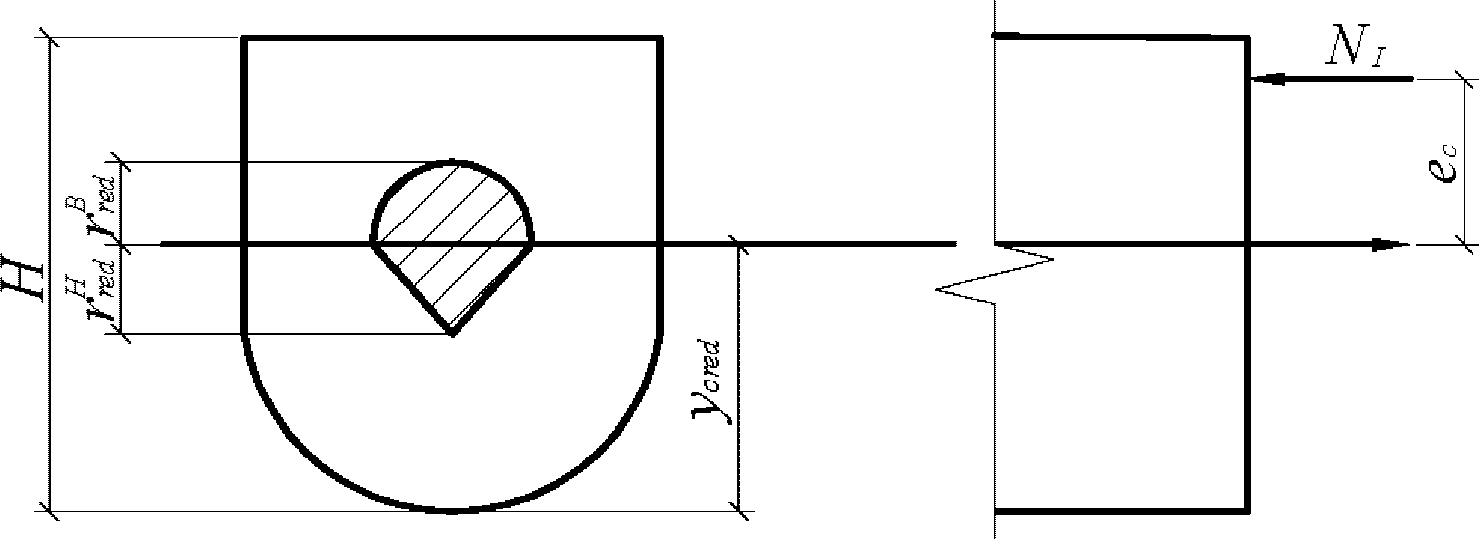
Для расчета по первой группе предельных состояний первоначально необходимо определить положение сжимающей силы относительно центра тяжести полного приведенного сечения, а также определить ядровые расстояния
(рисунок 4.4)
.
При попадании сжимающей силы в ядро сечения производится расчет по прочности в случае малых эксцентриситетов (расчет по прочности на сжатие) и расчет по устойчивости.
При выходе сжимающей силы из ядра сечения производится расчет по прочности в случае больших эксцентриситетов.
Случай малых эксцентриситетов определяет следующие условия:
или
В
формулах (4.1)
-
(4.2)
:
e
c
- эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения
(рисунок 4.5)
, м;
N
I
- продольное сжимающее усилие от расчетных нагрузок
(рисунок 4.5)
, кН.
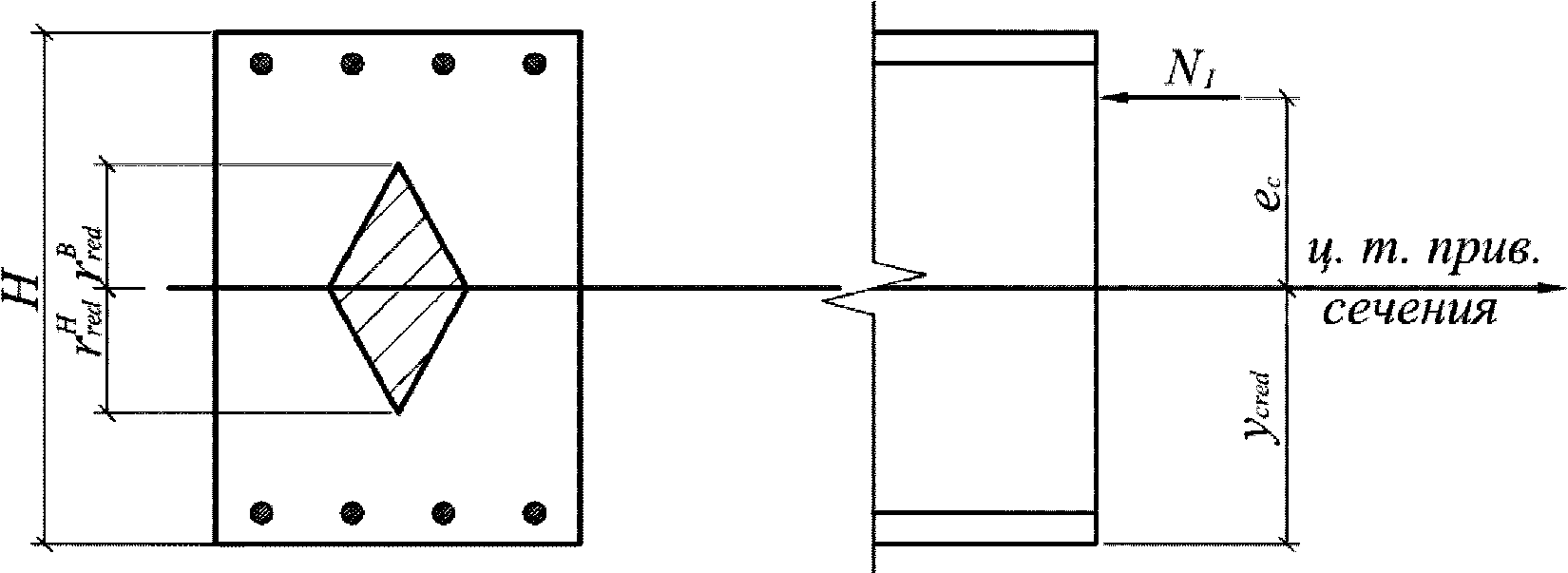
Случай больших эксцентриситетов определяет следующие условия:
e
c
> 0 и
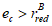 (4.3)
(4.3)
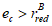 (4.3)
(4.3)
или
e
c
< 0 и
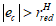 . (4.4)
. (4.4)
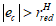 . (4.4)
. (4.4)
Для удобства расчета вводится понятие "ось определения усилий". Ось определения усилий - это такая ось, относительно которой производится сбор усилий. Такое допущение необходимо в связи с тем, что часто проектировщик не может заранее знать положение центра тяжести приведенного сечения (особенно для сложных, несимметричных сечений). Параметры
N
I
и
M
I
рассчитываются относительно оси определения усилий.
Эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения
e
c
для статически определимых систем вычисляется по формулам:
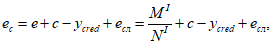 (4.6)
(4.6)
при
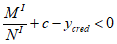 , (4.7)
, (4.7)
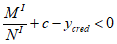 , (4.7)
, (4.7)
В
формулах (4.5)
-
(4.8)
:
e
- эксцентриситет продольной силы
N
I
относительно оси определения усилий, м
(рисунок 4.6)
;
e
сл
- случайный эксцентриситет
(рисунок 4.6)
, м;
c
- расстояние между нижней гранью сечения и осью определения усилий
(рисунок 4.6)
, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
(рисунок 4.6)
, м;
M
I
=
N
I
e
- изгибающий момент от действия расчетных нагрузок, кНм.

относительно центра тяжести полного приведенного сечения
Эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения
e
c
для статически неопределимых систем вычисляется по формулам:
при
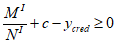 , (4.9)
, (4.9)
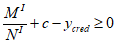 , (4.9)
, (4.9)
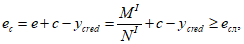 (4.10)
(4.10)
при
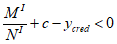 , (4.11)
, (4.11)
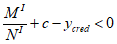 , (4.11)
, (4.11)
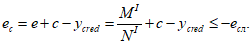 (4.12)
(4.12)
Случайный эксцентриситет
e
сл
определяется по формуле:
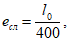 (4.13)
(4.13)
где
l
0
- геометрическая длина элемента или ее часть между точками закрепления, принимаемая согласно
п. 7.52
СП 35.13330, м.
Расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
y
cred
определяется по формуле:
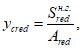 (4.13)
(4.13)
где
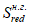 - приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
- приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
A
red
- приведенная площадь полного сечения, м
2
.
Приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения
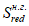 , определяется по формуле:
, определяется по формуле:
В
формулах (4.14)
-
(4.15)
:
n
1
- коэффициент приведения армирования к бетону;
i
- номер ряда армирования;
m
- количество рядов армирования;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. В таком случае статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения
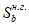 , определяется по формуле:
, определяется по формуле:
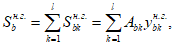 (4.16)
(4.16)
где
k
- номер участка сечения;
l
- количество участков сечения;
А
bk
- площадь
k
-го участка сечения
(рисунок 4.7)
, м
2
;
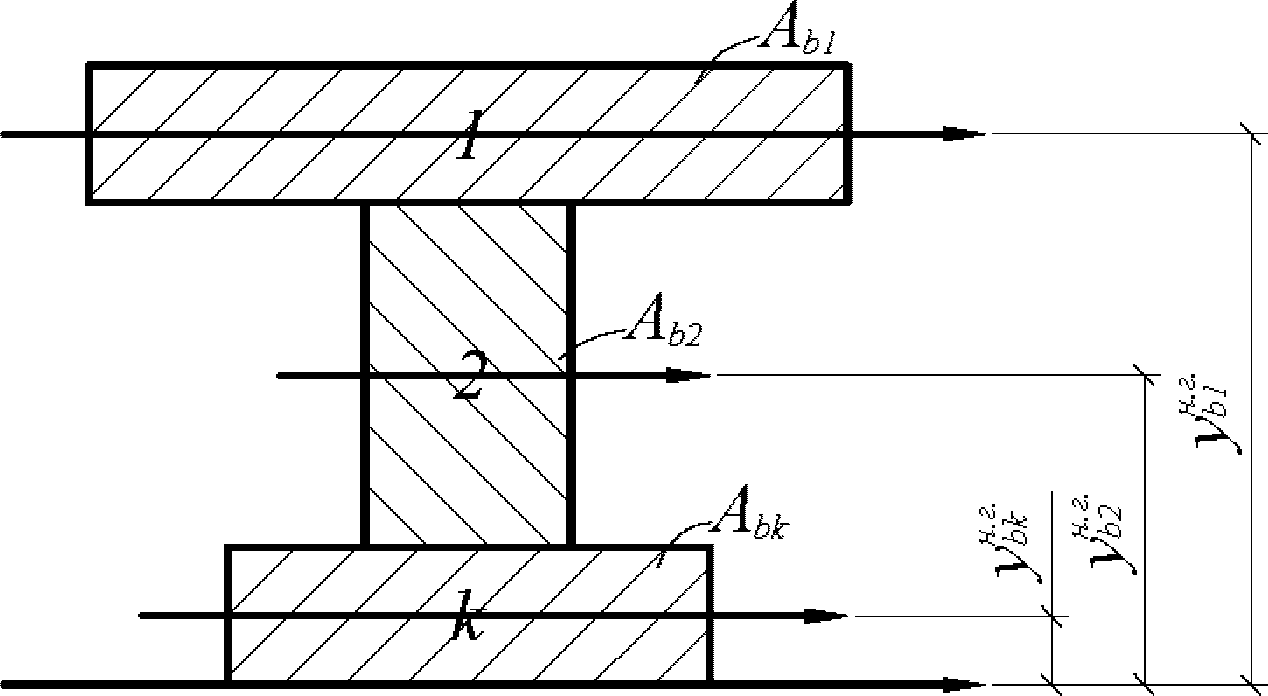
Статический момент инерции
i
-го ряда армирования, взятый относительно нижней грани сечения
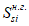 , определяется по формуле:
, определяется по формуле:
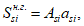 (4.17)
(4.17)
где
A
si
- площадь
i
-го ряда армирования, м
2
;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м.
Приведенная площадь полного сечения
A
red
определяется по формуле:
В
формулах (4.18)
-
(4.19)
:
A
b
- площадь бетонной части сечения, м
2
.
Расчет ядрового расстояния вблизи верхней грани сечения
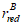 и ядрового расстояния вблизи нижней грани сечения
и ядрового расстояния вблизи нижней грани сечения
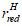 , осуществляется по формулам:
, осуществляется по формулам:
В
формулах (4.20)
-
(4.21)
:
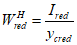 - момент сопротивления по нижней грани сечения, м
3
;
- момент сопротивления по нижней грани сечения, м
3
;
I
red
- момент инерции полного приведенного сечения, взятый относительно центра тяжести полного приведенного сечения, м
4
;
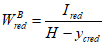 - момент сопротивления по верхней грани сечения, м
3
;
- момент сопротивления по верхней грани сечения, м
3
;
H
- высота сечения, м.
Момент инерции полного приведенного сечения, взятый относительно центра тяжести полного приведенного сечения
I
red
, определяется по формулам:
I
si
=
A
si
(
a
si
-
y
cred
)
2
, (4.23)
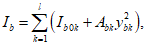 (4.24)
(4.24)
В
формулах (4.22)
-
(4.25)
:
I
b
- момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения, м
4
;
I
s
- момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения, м
4
;
I
b
0
k
- собственный момент инерции
k
-го участка сечения, м
4
;
y
bk
- расстояние между центром тяжести
k
-го участка и центром тяжести полного приведенного сечения, м.
Расчет по прочности в случае больших эксцентриситетов необходимо производить с учетом коэффициента влияния прогиба по прочности
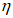 при условии, что внутренние усилия в системе определены по недеформируемой схеме. Если внутренние усилия определены с учетом деформаций системы, то
при условии, что внутренние усилия в системе определены по недеформируемой схеме. Если внутренние усилия определены с учетом деформаций системы, то
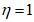 (рисунок 4.8)
.
(рисунок 4.8)
.
┌───────────────────────────────┐
│ Расчеты по прочности в случае │
│ больших эксцентриситетов │
└────────────────┬──────────────┘
┌────────────────┴──────────────┐
│ Расчет коэффициента влияния │
│ прогиба по прочности │
└────────────────┬──────────────┘
┌────────────────┴──────────────┐
│ Расчет по прочности в случае │
│ больших эксцентриситетов │
└───────────────────────────────┘
в случае больших эксцентриситетов
Для железобетонных элементов, имеющих несмещаемые опоры и опоры, одинаково перемещающиеся при вынужденных деформациях (например, при температурных удлинениях), коэффициент влияния прогиба по прочности
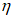 для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
при
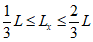 , (4.26)
, (4.26)
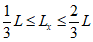 , (4.26)
, (4.26)
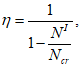 (4.27)
(4.27)
где
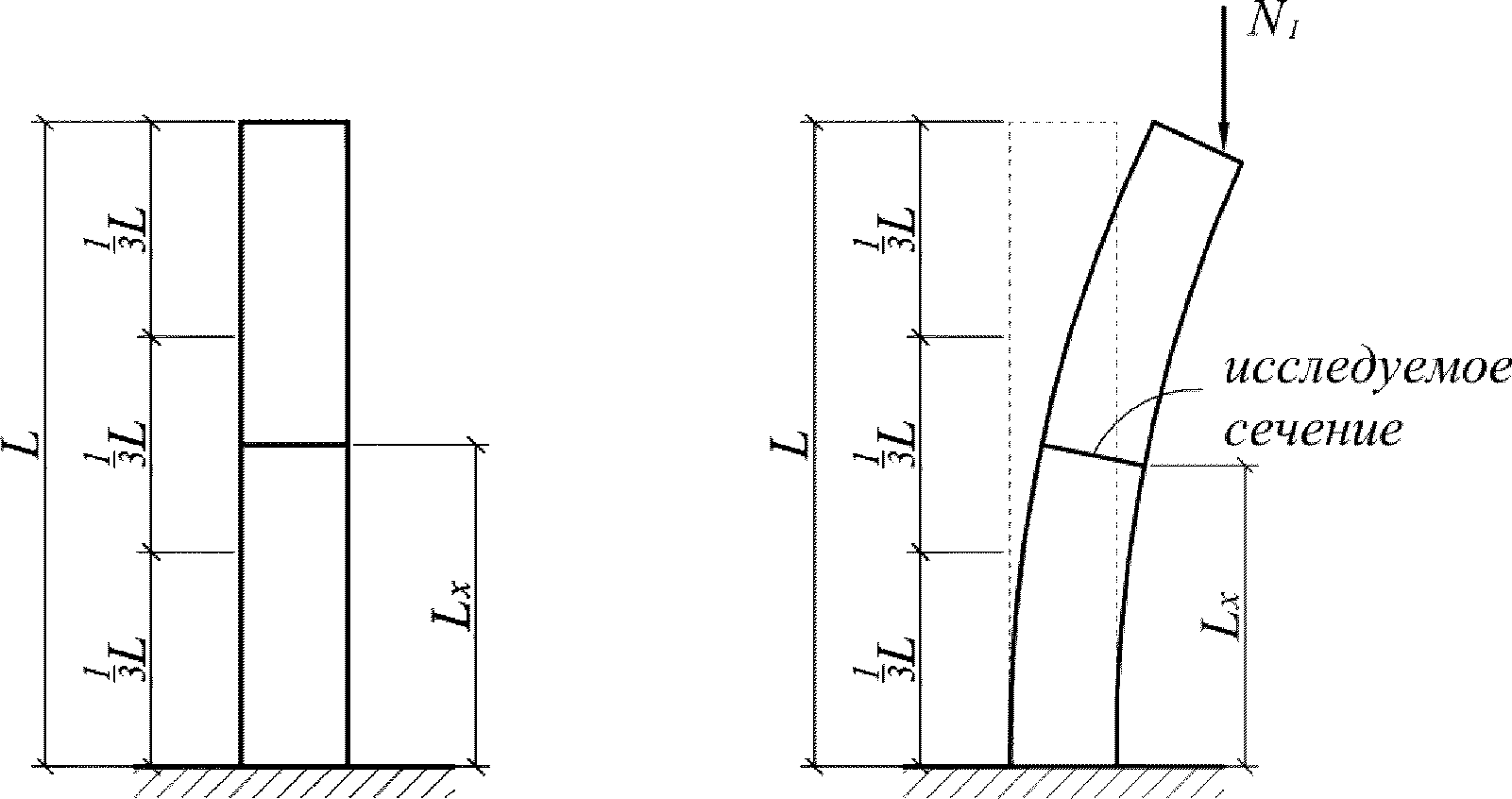
L
- длина рассматриваемого элемента или участка между точками закрепления
(рисунок 4.9)
, м;
L
x
- расстояние от точки закрепления элемента до рассматриваемого сечения
(рисунок 4.9)
, м;
N
I
- продольное сжимающее усилие от постоянных и временных расчетных нагрузок
(рисунок 4.9)
, кН;
N
cr
- условная критическая сила для железобетонного элемента, кН.
коэффициента влияния прогиба по прочности
Коэффициент влияния прогиба по прочности
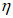 для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
при
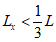 , (4.28)
, (4.28)
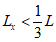 , (4.28)
, (4.28)
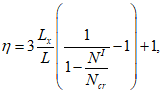 (4.29)
(4.29)
при
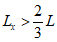 , (4.30)
, (4.30)
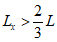 , (4.30)
, (4.30)
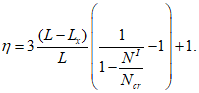 (4.31)
(4.31)
В запас прочности допускается определять коэффициент влияния прогиба по прочности
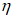 по формуле:
по формуле:
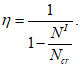 (4.32)
(4.32)
Условная критическая сила для железобетонного элемента
N
cr
определяется по формуле:
В
формулах (4.33)
-
(4.34)
:
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
l
0
- геометрическая длина элемента или ее часть между точками закрепления, принимаемая согласно
п. 7.52
СП 35.13330, м;
I
b
- момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения согласно
4.1.1
, м
4
;
n
1
- коэффициент приведения армирования к бетону;
I
s
- момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения согласно
4.1.1
, м
4
;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
.
Эксцентриситет продольной силы
N
Il
относительно центра тяжести полного приведенного сечения
e
cl
для статически определимых систем определяется по формулам:
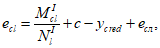 (4.36)
(4.36)
при
e
c
< 0 (4.37)
В
формулах (4.35)
-
(4.38)
:
e
c
- эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения согласно
4.1.1
, м;
c
- расстояние между нижней гранью сечения и осью определения усилий, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения согласно
4.1.1
, м;
e
сл
- случайный эксцентриситет согласно
4.1.1
, м.
Эксцентриситет продольной силы
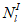 относительно центра тяжести полного приведенного сечения
e
cl
для статически неопределимых систем определяется по формулам:
относительно центра тяжести полного приведенного сечения
e
cl
для статически неопределимых систем определяется по формулам:
при
e
c
>= 0 (4.39)
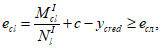 (4.40)
(4.40)
при
e
c
< 0 (4.41)
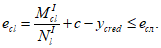 (4.42)
(4.42)
Если
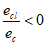 , то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
, то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
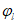 , определяется исходя из условий:
, определяется исходя из условий:
при |
e
c
| < 0,1
H
, (4.45)
В
формулах (4.43)
-
(4.46)
:
H
- высота сечения, м.
Если
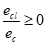 , то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
, то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
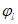 , определяется по формуле:
, определяется по формуле:
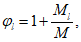 (4.47)
(4.47)
где
M
l
- изгибающий момент от действия постоянных расчетных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм;
M
- изгибающий момент от действия постоянных и временных расчетных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм.
Изгибающие моменты от действия постоянных и временных расчетных нагрузок и полный изгибающий момент, взятые относительно наиболее растянутой или наименее сжатой грани сечения, определяются по формулам:
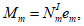 (4.49)
(4.49)
В
формулах (4.48)
-
(4.50)
:
e
l
- эксцентриситет продольной силы
N
Il
относительно наиболее растянутой или наименее сжатой грани сечения, м;
M
m
- изгибающий момент от действия временных расчетных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм;
e
m
- эксцентриситет продольной силы
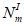 относительно наиболее растянутой или наименее сжатой грани сечения, м;
относительно наиболее растянутой или наименее сжатой грани сечения, м;
e
- эксцентриситет продольной силы
N
относительно наиболее растянутой или наименее сжатой грани сечения, м.
Эксцентриситеты продольных сил относительно наиболее растянутой или наименее сжатой грани сечения для статически определимых систем вычисляются по формулам:
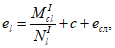 (4.52)
(4.52)
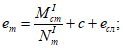 (4.53)
(4.53)
при
e
c
< 0, (4.54)
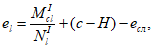 (4.55)
(4.55)
В
формулах (4.51)
-
(4.56)
:
Эксцентриситет продольной силы
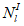 относительно наиболее растянутой или наименее сжатой грани сечения
e
l
для статически неопределимых систем вычисляется по формулам:
относительно наиболее растянутой или наименее сжатой грани сечения
e
l
для статически неопределимых систем вычисляется по формулам:
при
e
c
> 0 и
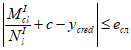 , (4.57)
, (4.57)
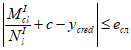 , (4.57)
, (4.57)
e
l
=
y
cred
+
e
сл
, (4.58)
при
e
c
> 0 и
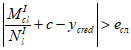 , (4.59)
, (4.59)
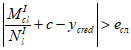 , (4.59)
, (4.59)
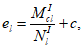 (4.60)
(4.60)
при
e
c
< 0 и
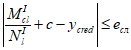 , (4.61)
, (4.61)
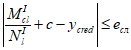 , (4.61)
, (4.61)
e
l
=
y
cred
-
H
-
e
сл
, (4.62)
при
e
c
< 0 и
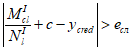 , (4.63)
, (4.63)
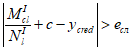 , (4.63)
, (4.63)
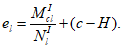 (4.64)
(4.64)
Эксцентриситет продольной силы
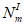 относительно наиболее растянутой или наименее сжатой грани сечения
e
m
для статически неопределимых систем вычисляется по формулам:
относительно наиболее растянутой или наименее сжатой грани сечения
e
m
для статически неопределимых систем вычисляется по формулам:
e
m
=
y
cred
+
e
сл
, (4.66)
при
e
c
> 0 и
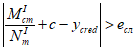 , (4.67)
, (4.67)
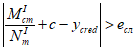 , (4.67)
, (4.67)
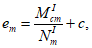 (4.68)
(4.68)
при
e
c
< 0 и
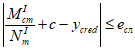 , (4.69)
, (4.69)
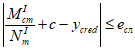 , (4.69)
, (4.69)
e
m
=
y
cred
-
H
-
e
сл
, (4.70)
при
e
c
< 0 и
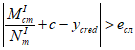 , (4.71)
, (4.71)
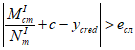 , (4.71)
, (4.71)
В
формулах (4.65)
-
(4.72)
:
Эксцентриситет продольной силы
N
I
относительно наиболее растянутой или наименее сжатой грани сечения
e
определяется по формуле:
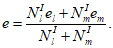 (4.73)
(4.73)
Коэффициент
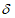 определяется по формуле:
определяется по формуле:
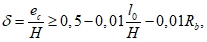 (4.74)
(4.74)
где
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330 (в формулу подставляется в МПа).
В выше приведенных формулах моменты со знаком "+" растягивают нижнюю грань элемента и сжимают верхнюю. Моменты со знаком "-" растягивают верхнюю грань элемента и сжимают нижнюю.
Эксцентриситет со знаком "+" указывает на расположение продольной силы выше центра тяжести полного приведенного сечения. Эксцентриситет со знаком "-" указывает на расположение продольной силы ниже центра тяжести полного приведенного сечения.
Расчет по прочности в случае больших эксцентриситетов рекомендуется производить с использованием нелинейной деформационной модели и руководствуясь следующими предпосылками:
- сопротивление бетона растяжению принимается равным нулю;
- диаграммы деформирования бетона и арматуры двух- или трехлинейные;
- эпюра относительных деформаций имеет линейный вид;
- для удобства расчетов принять верхнюю грань элемента наиболее сжатой, а нижнюю - наиболее растянутой (наименее сжатой).
При
e
c
> 0 верхняя грань сечения является наиболее сжатой и к расчету принимается нормально ориентированное сечение. При
e
c
< 0 нижняя грань сечения является наиболее сжатой и к расчету принимается обратное сечение (повернутое на 180°)
(рисунок 4.10)
.
e
c
- эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения согласно
4.1.1
, м.
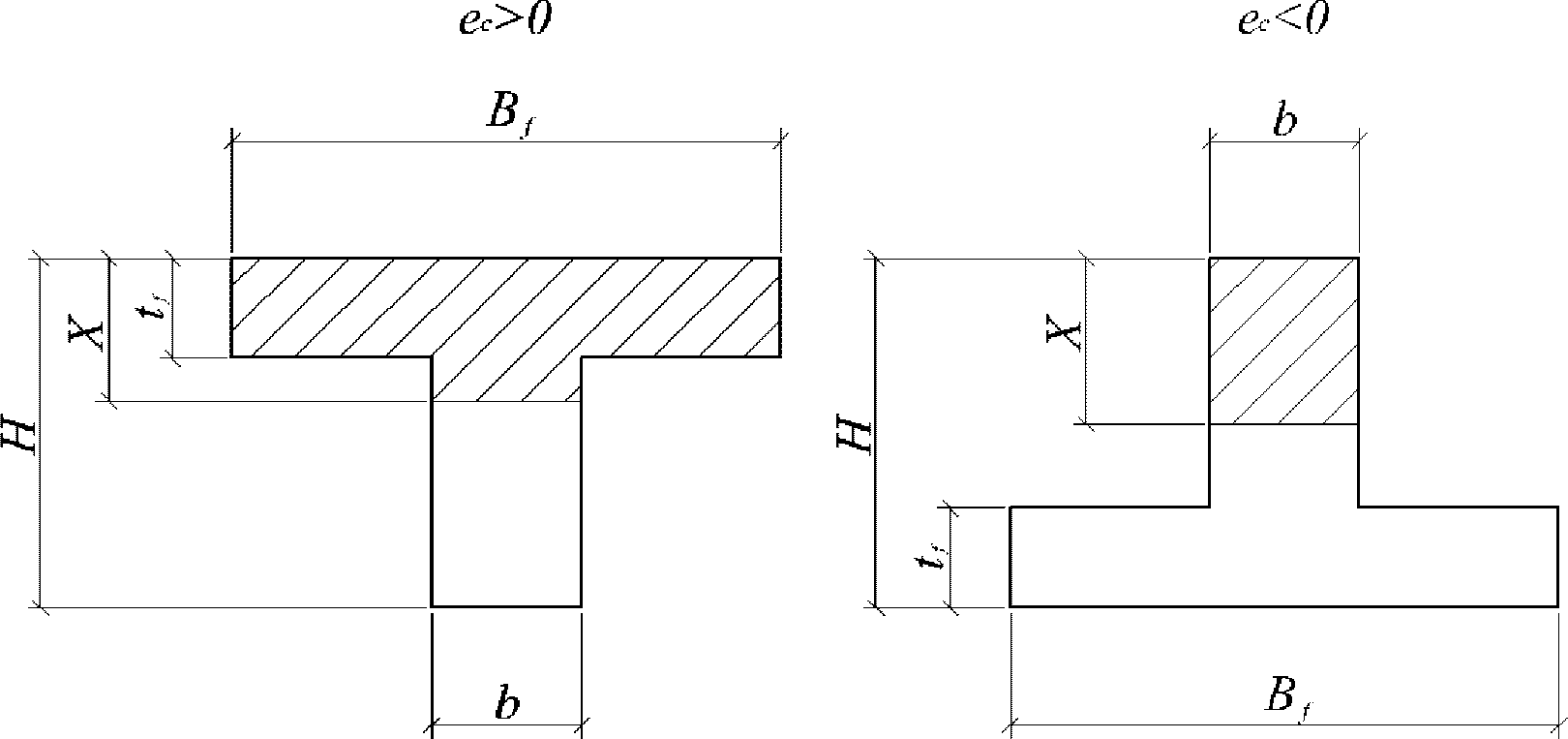
в зависимости от эксцентриситета силы
N
I
Предварительно сечение по высоте разбивается на элементарные участки с определенным шагом
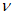 . Каждому участку присваивается порядковый номер - сверху вниз
(рисунок 4.11)
.
. Каждому участку присваивается порядковый номер - сверху вниз
(рисунок 4.11)
.
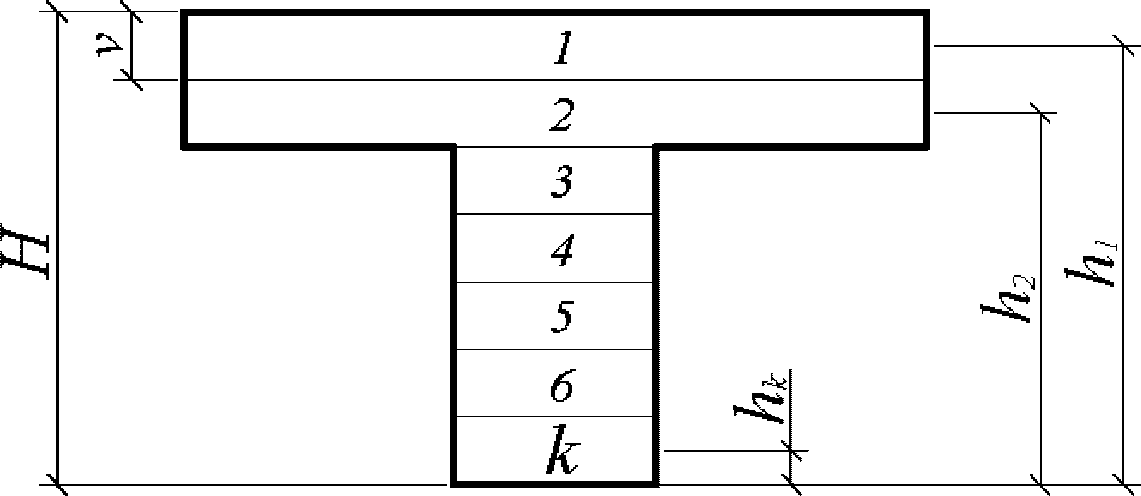
на элементарные участки
В общем случае расчет рекомендуется производить при помощи компьютерных средств путем подбора такой высоты сжатой зоны бетона
X
, при которой наблюдается равновесие системы:
где
k
- номер элементарного участка сечения;
l
- количество элементарных участков сечения;
N
bk
- усилие, возникающее в
k
-ом элементарном участке, кН;
i
- номер ряда армирования;
m
- количество рядов армирования;
N
si
- усилие, возникающее в
i
-ом ряду армирования, кН;
N
I
- продольное сжимающее усилие от расчетных нагрузок (вводится в формулу со знаком плюс), кН.
Возможны три варианта разрушения железобетонного сечения. Первый вариант предполагает разрушение сечения по растянутой арматуре, когда в одном из рядов армирования достигается предельная деформация растяжения арматуры
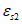 . Второй вариант предполагает разрушение сечения по сжатому бетону, когда достигается предельная деформация сжатия бетона
. Второй вариант предполагает разрушение сечения по сжатому бетону, когда достигается предельная деформация сжатия бетона
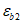 . Третий вариант предполагает одновременное разрушение сечения по растянутой арматуре и сжатому бетону, когда предельная деформация растяжения арматуры
. Третий вариант предполагает одновременное разрушение сечения по растянутой арматуре и сжатому бетону, когда предельная деформация растяжения арматуры
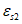 и предельная деформация сжатия бетона
и предельная деформация сжатия бетона
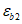 достигаются одновременно. Значение высоты сжатой зоны бетона
X
, при третьем варианте развития событий называется граничной высотой сжатой зоны бетона
X
r
. Граничная высота сжатой зоны бетона
X
r
позволяет определить вариант разрушения сечения.
достигаются одновременно. Значение высоты сжатой зоны бетона
X
, при третьем варианте развития событий называется граничной высотой сжатой зоны бетона
X
r
. Граничная высота сжатой зоны бетона
X
r
позволяет определить вариант разрушения сечения.
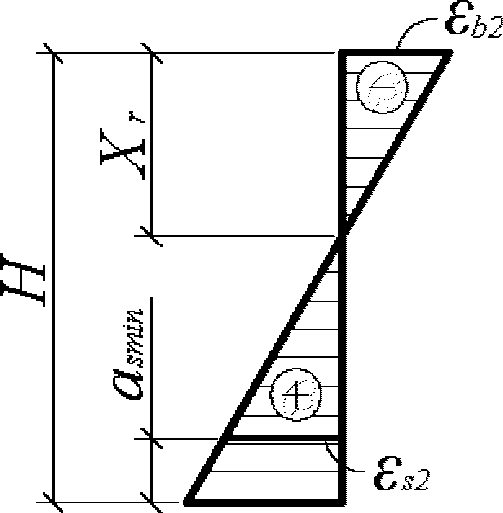
Граничная высота сжатой зоны бетона
X
r
определяется геометрически по эпюре относительных деформаций сечения
(рисунок 4.12)
:
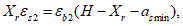 (4.77)
(4.77)
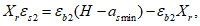 (4.78)
(4.78)
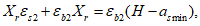 (4.79)
(4.79)
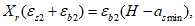 (4.80)
(4.80)
В
формулах (4.76)
-
(4.81)
:
H
- высота сечения
(рисунок 4.12)
, м;
a
s
min
- расстояние между наиболее растянутой гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования
(рисунок 4.12)
, м;
для расчета граничной высоты сжатой зоны бетона
Для удобства расчетов вводятся следующие условия:
при
X
<=
X
r
- первый вариант разрушения (разрушение по растянутой арматуре) или третий (одновременное разрушение сечения по арматуре и бетону);
при
X
>
X
r
- второй вариант разрушения (разрушение по сжатому бетону).
Усилия, возникающие в каждом элементарном участке
N
bk
, а также в каждом ряду армирования
N
si
, определяют по формулам:
В
формулах (4.82)
-
(4.83)
:
A
si
- площадь
i
-го ряда армирования, м
2
;
Напряжения в элементарных участках бетонного сечения и рядах армирования определяются по диаграммам деформирования бетона и арматуры
(рисунок 4.13)
. Для упрощения расчетов допускается использовать двухлинейные диаграммы деформирования.
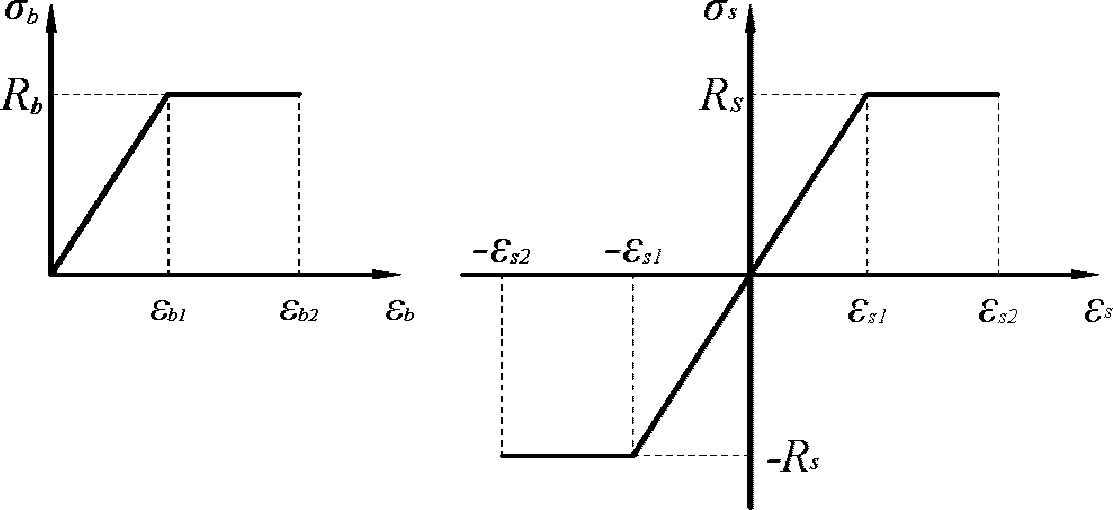
(слева) и арматуры (справа)
Для бетона двухлинейными диаграммами деформирования вводятся следующие условия:
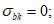 (4.85)
(4.85)
при
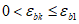 , (4.86)
, (4.86)
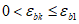 , (4.86)
, (4.86)
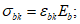 (4.87)
(4.87)
при
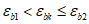 , (4.88)
, (4.88)
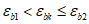 , (4.88)
, (4.88)
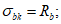 (4.89)
(4.89)
В
формулах (4.84)
-
(4.90)
:
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
Для арматуры двухлинейными диаграммами деформирования вводятся следующие условия:
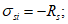 (4.92)
(4.92)
при
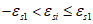 , (4.93)
, (4.93)
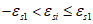 , (4.93)
, (4.93)
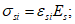 (4.94)
(4.94)
при
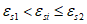 , (4.95)
, (4.95)
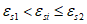 , (4.95)
, (4.95)
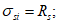 (4.96)
(4.96)
В
формулах (4.91)
-
(4.97)
:
R
s
- расчетное сопротивление арматуры согласно
таблице 7.16
СП 35.13330, кН/м
2
;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
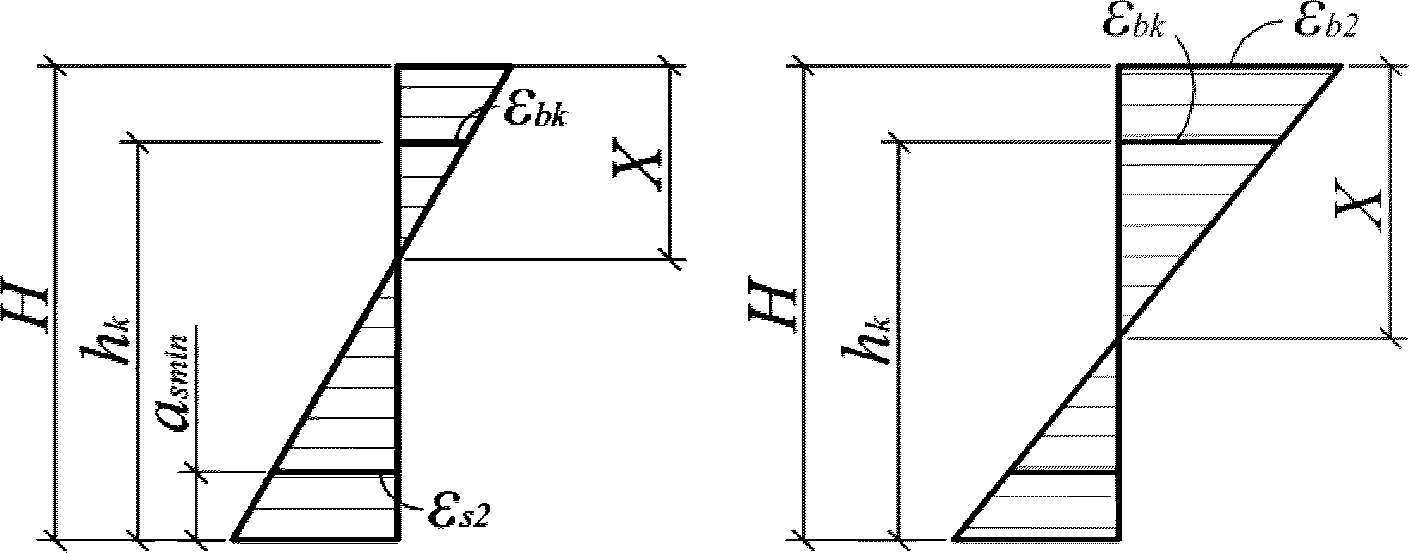
Относительные деформации
k
-го элементарного участка бетонного сечения, определяются геометрически
(рисунок 4.14)
:
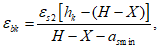 (4.99)
(4.99)
при
X
>
X
r
, (4.100)
В
формулах (4.98)
-
(4.101)
:
h
k
- расстояние между нижней гранью сечения и центром
k
-го элементарного участка
(рисунок 4.14)
, м.
(слева - случай разрушения по арматуре, справа - по бетону)
Относительные деформации
i
-го ряда армирования определяются геометрически
(рисунок 4.15)
:
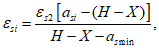 (4.103)
(4.103)
при
X
>
X
r
, (4.104)
В
формулах (4.102)
-
(4.105)
:
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования
(рисунок 4.15)
, м.
(слева - случай разрушения по арматуре, справа - по бетону)
Расстояние между нижней гранью сечения и центром
k
-го элементарного участка бетонного сечения при нумерации участков сверху вниз от 1 и далее, допускается определять по формуле:
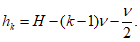 (4.106)
(4.106)
После определения высоты сжатой зоны бетона
X
, при которой соблюдается
условие (4.75)
, производится расчет предельного изгибающего усилия
M
ult
:
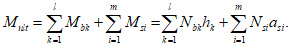 (4.107)
(4.107)
Расчет внецентренно сжатого элемента по прочности в случае больших эксцентриситетов производится из условия:
N
I
e
0
<=
M
ult
, (4.108)
где
e
0
- эксцентриситет продольной силы
N
I
относительно равнодействующей усилий в растянутой арматуре
(рисунок 4.16)
, м.
Эксцентриситет продольной силы
N
I
относительно равнодействующей усилий в растянутой арматуре
e
0
, определяется по формулам:
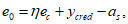 (4.110)
(4.110)
при
e
c
< 0, (4.111)
В
формулах (4.109)
-
(4.112)
:
e
c
- эксцентриситет продольной силы
N
I
относительно центра тяжести полного приведенного сечения согласно
4.1.1
(рисунок 4.16)
, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения согласно
4.1.1
(рисунок 4.16)
, м;
a
s
- расстояние между нижней гранью сечения и равнодействующей усилий в растянутой арматуре
(рисунок 4.16)
, м.
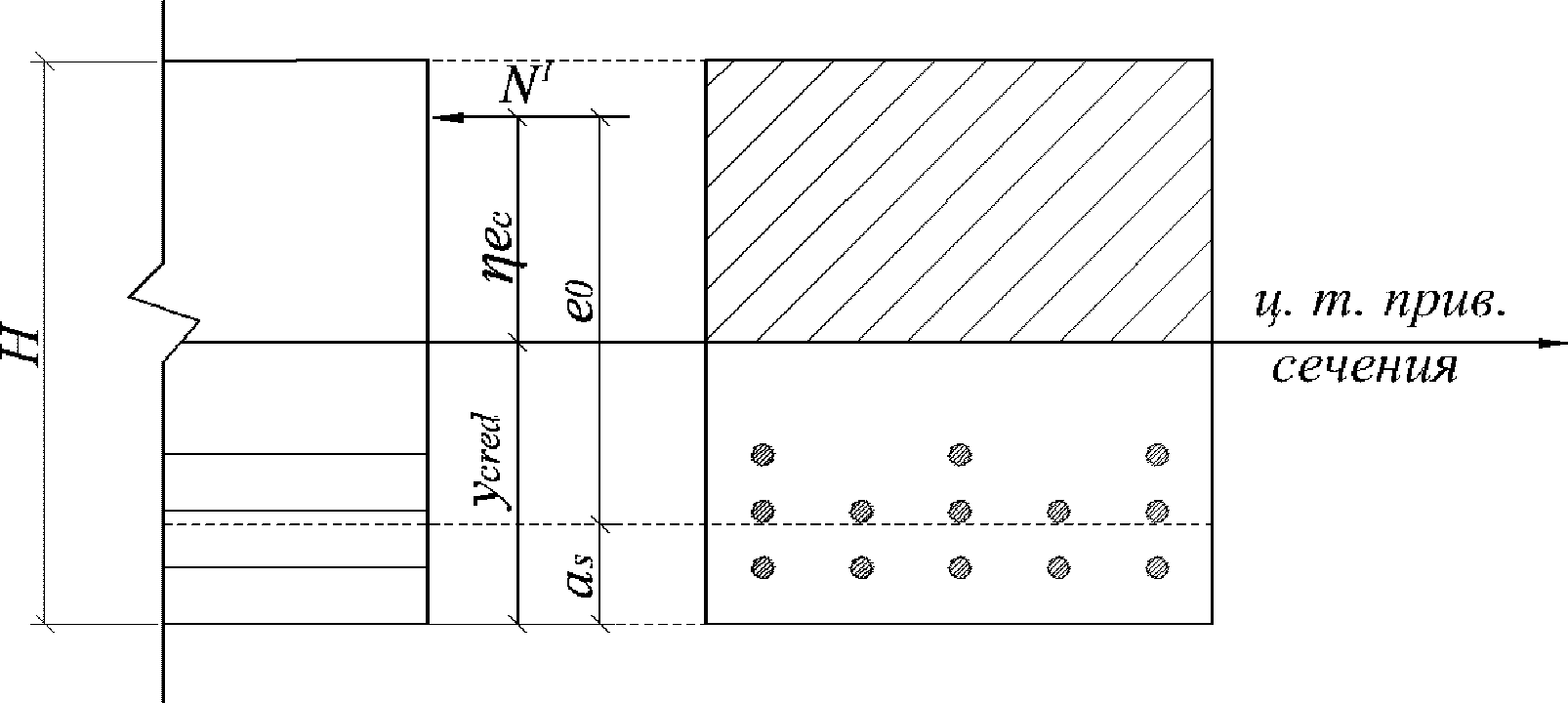
Расстояние между нижней гранью сечения и равнодействующей усилий в растянутой арматуре
a
s
определяется по формуле:
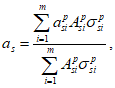 (4.113)
(4.113)
где
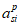 - расстояние между нижней гранью сечения и центром тяжести
i
-го растянутого ряда армирования, м;
- расстояние между нижней гранью сечения и центром тяжести
i
-го растянутого ряда армирования, м;
Для удобства расчетов вводится следующий критерий определения состояния арматуры:
при
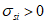 ,
,
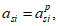 (4.114)
(4.114)
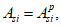 (4.115)
(4.115)
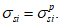 (4.116)
(4.116)
Расчеты рекомендуется производить в табличном виде
(рисунок 4.17)
.
|
|
Параметры бетона
|
|||||||||
|
N
|
h
bk
|
A
bk
|
|
|
N
bk
|
M
bk
|
||||
|
п/п
|
м
|
м
2
|
-
|
кПа
|
кН
|
кНм
|
||||
|
|
|
1
|
|
|
|
|
|
|
||
|
|
|
2
|
|
|
|
|
|
|
||
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
||
|
|
|
5
|
|
|
|
|
|
|
||
|
|
|
6
|
|
|
|
|
|
|
||
|
|
|
k
|
|
|
|
|
|
|
||
|
|
|
|
||||||||
|
Параметры арматуры
|
||||||||
|
N
|
a
si
|
A
si
|
|
|
N
si
|
M
si
|
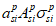
|
|
|
п/п
|
м
|
м
2
|
-
|
кПа
|
кН
|
кНм
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
i
|
|
|
|
|
|
|
|
|
|
|
|
|
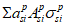
|
|
||||
Расчет внецентренно сжатых элементов по прочности в случае малых эксцентриситетов производится из условия:
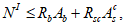 (4.117)
(4.117)
 если
если
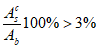 . (4.118)
. (4.118)
В
формулах (3.26)
-
(3.29)
:
N
I
- продольное сжимающее усилие от расчетных нагрузок
(рисунок 4.18)
, кН;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
A
b
- полная площадь сечения элемента
(рисунок 4.18)
, м
2
;
R
sc
- расчетное сопротивление арматуры сжатию согласно
п. 7.38
СП 35.13330, кН/м
2
;
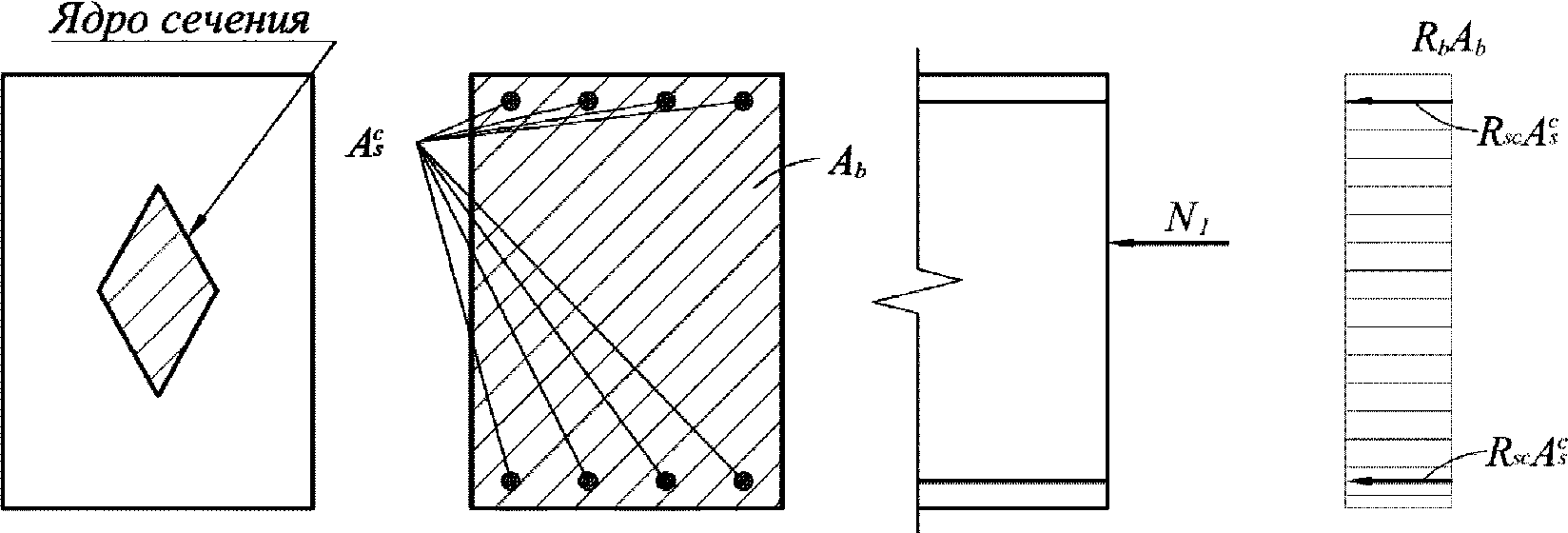
сжатого элемента в случае малых эксцентриситетов
Перед расчетом по устойчивости необходимо определить коэффициент продольного изгиба
(рисунок 4.19)
.
┌─────────────────────┐
│ Расчеты │
│ по устойчивости │
└──────────┬──────────┘
┌──────────┴──────────┐
│ Расчет коэффициента │
│ продольного изгиба │
└──────────┬──────────┘
┌──────────┴──────────┐
│ Расчет │
│ по устойчивости │
└─────────────────────┘
Коэффициент продольного изгиба
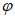 определяется по формуле:
определяется по формуле:
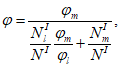 (4.119)
(4.119)
где
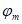 - коэффициент продольного изгиба, учитывающий воздействие временных нагрузок;
- коэффициент продольного изгиба, учитывающий воздействие временных нагрузок;
N
I
- продольное сжимающее усилие от расчетных нагрузок, кН;
Коэффициенты продольного изгиба
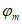 и
и
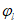 определяются по
таблице 7.21
СП 35.13330 в зависимости от гибкости элемента
определяются по
таблице 7.21
СП 35.13330 в зависимости от гибкости элемента
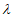 . Гибкость
. Гибкость
 определяется по формуле:
определяется по формуле:
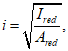 (4.121)
(4.121)
где
l
0
- геометрическая длина элемента или ее часть между точками закрепления, принимаемая согласно
п. 7.52
СП 35.13330, м;
i
- радиус инерции сечения, м;
I
red
- момент инерции полного приведенного сечения, взятый относительно центра тяжести полного приведенного сечения согласно
4.1.1
, м
4
;
A
red
- приведенная площадь полного сечения согласно
4.1.1
, м
2
.
Расчет внецентренно сжатых элементов по устойчивости производится из условия:
В
формулах (4.122)
-
(4.123)
:
N
I
- продольное сжимающее усилие от расчетных нагрузок, кН;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
A
b
- полная площадь сечения элемента, м
2
;
R
sc
- расчетное сопротивление арматуры сжатию согласно
п. 7.38
СП 35.13330, кН/м
2
;
Перед расчетом по выносливости необходимо произвести анализ напряженно-деформированного состояния сечения, расчет коэффициента влияния прогиба по прочности (не обязательно), расчет геометрических характеристик сечения
(рисунок 4.20)
.
┌───────────────────┐
│ Расчеты │
│ по выносливости │
└─────────┬─────────┘
┌──────────────────────┴───────────────────────┐
│ Анализ напряженно-деформированного │
│ состояния сечения │
└──────────────────────┬───────────────────────┘
┌──────────────────────┴───────────────────────┐
│ Расчет коэффициента влияния прогиба │
│ по прочности (не обязательно) │
└──────────────────────┬───────────────────────┘
┌──────────────────────┴───────────────────────┐
│ Расчет геометрических характеристик сечения │
│ при расчетах по выносливости │
└──────────────────────┬───────────────────────┘
┌─────────┴─────────┐
│ Расчет │
│ по выносливости │
└───────────────────┘
Перед расчетом по выносливости необходимо получить усилия от двух загружений, одно из которых предполагает достижение максимальных нормальных напряжений в бетоне и арматуре, а второе - минимальных.
Анализ напряженно-деформированного состояния сечения заключается в определении состояния верхней и нижней граней сечения для первого и второго загружений.
При
e
cj
> 0 верхняя грань сечения является наиболее сжатой, а нижняя растянутой или наименее сжатой. В таком случае к расчету геометрических характеристик принимается нормально ориентированное сечение
(рисунок 4.21)
.
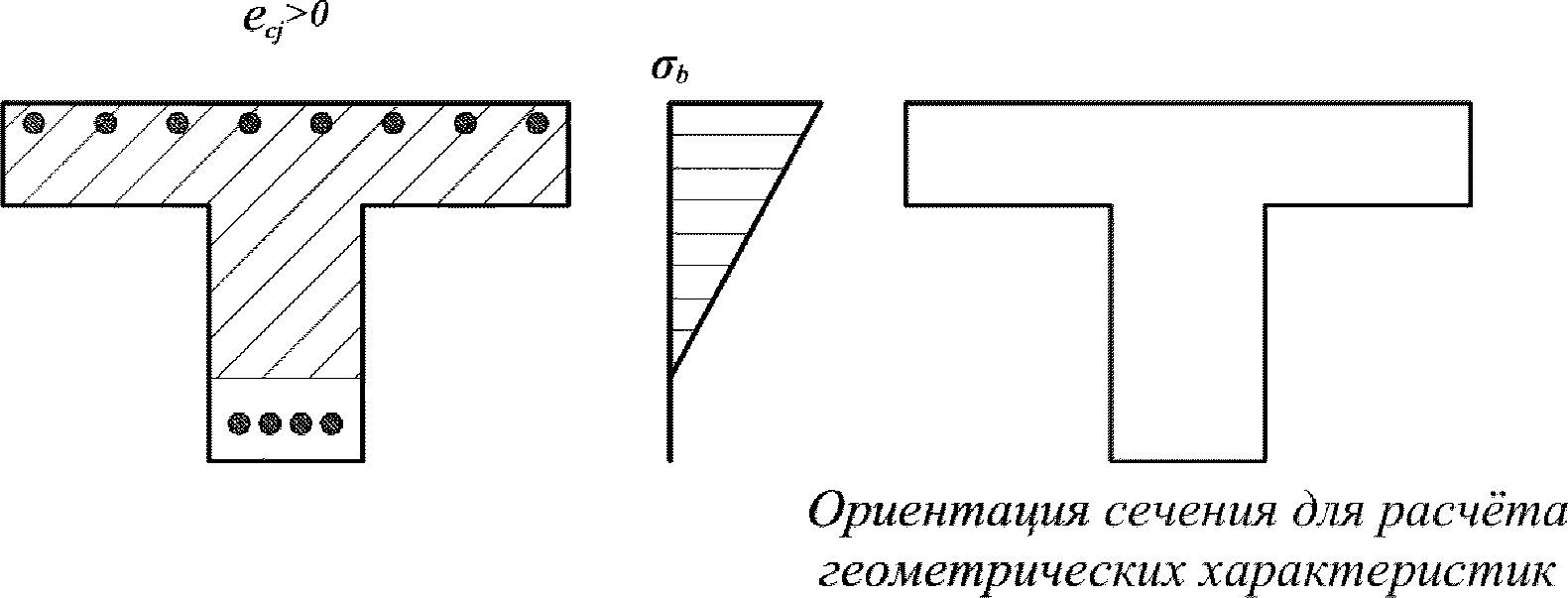
геометрических характеристик
При
e
cj
< 0 нижняя грань сечения является наиболее сжатой, а верхняя растянутой или наименее сжатой. В таком случае к расчету геометрических характеристик принимается обратное сечение (повернутое на 180°)
(рисунок 4.22)
.
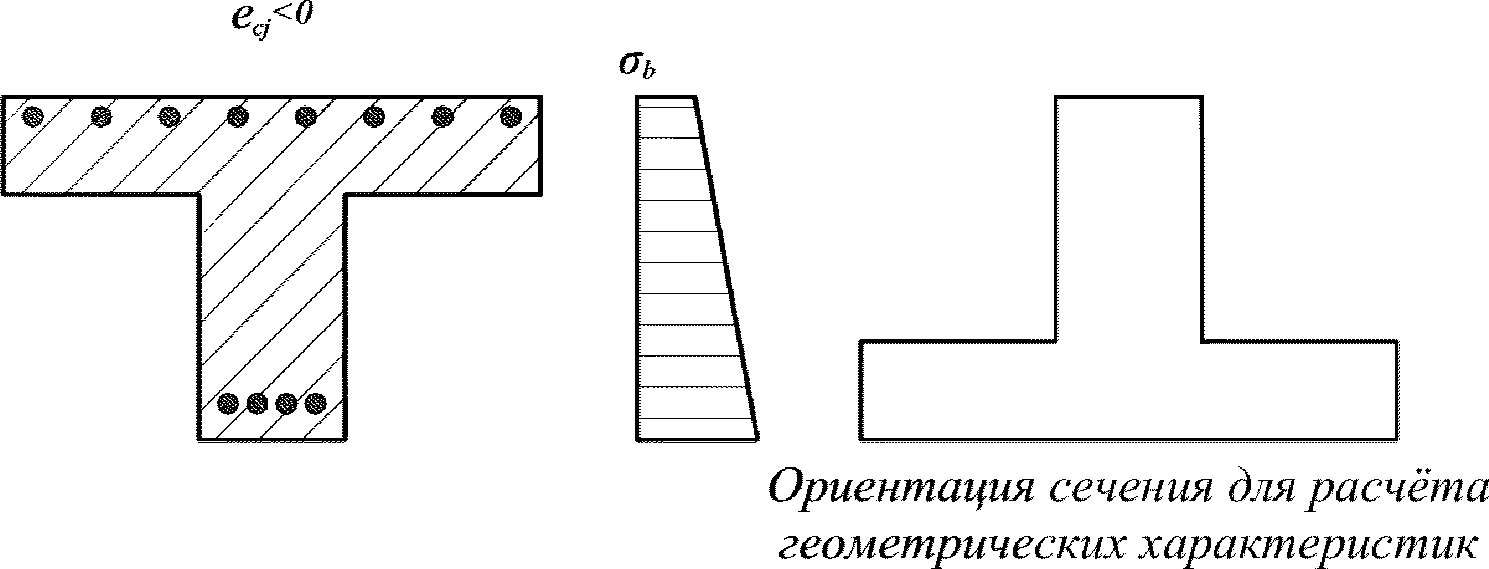
геометрических характеристик:
e
cj
- эксцентриситет продольной силы
 относительно
относительно
центра тяжести полного приведенного сечения, м;
j
- номер исследуемого загружения
Для удобства расчета вводится понятие "ось определения усилий". Ось определения усилий - это такая ось, относительно которой производится сбор усилий. Такое допущение необходимо в связи с тем, что часто проектировщик не может заранее знать положение центра тяжести приведенного сечения (особенно для сложных, несимметричных сечений). Параметры
 и
и
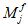 рассчитываются относительно оси определения усилий.
рассчитываются относительно оси определения усилий.
Эксцентриситет продольной силы
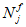 относительно центра тяжести полного приведенного сечения
e
cj
вычисляется по формуле:
относительно центра тяжести полного приведенного сечения
e
cj
вычисляется по формуле:
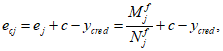 (4.124)
(4.124)
где
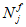 - продольное сжимающее усилие
j
-го загружения от нагрузок для расчета по выносливости, кН;
- продольное сжимающее усилие
j
-го загружения от нагрузок для расчета по выносливости, кН;
e
j
- эксцентриситет продольной силы
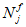 относительно оси определения усилий, для
j
-го
(рисунок 4.23)
, м;
относительно оси определения усилий, для
j
-го
(рисунок 4.23)
, м;
c
- расстояние между нижней гранью сечения и осью определения усилий, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
(рисунок 4.23)
, м;
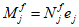 - изгибающий момент
j
-го загружения от действия нагрузок для расчета по выносливости, кНм.
- изгибающий момент
j
-го загружения от действия нагрузок для расчета по выносливости, кНм.
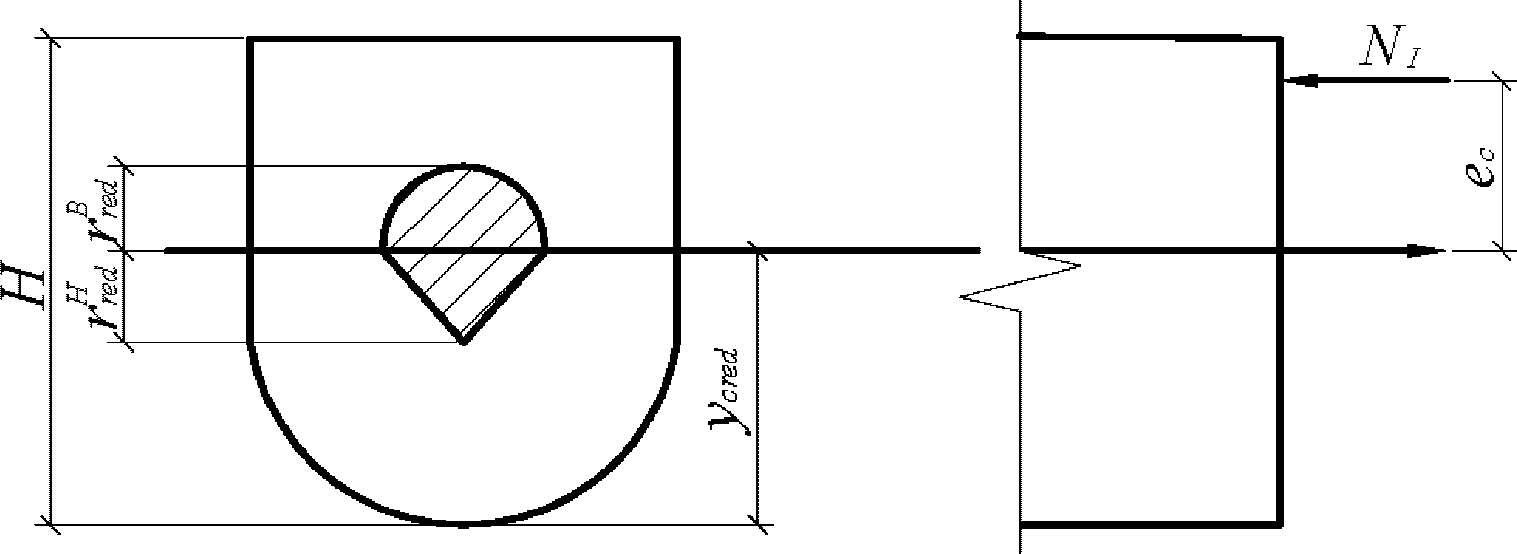
относительно центра тяжести полного приведенного сечения
Расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
y
cred
определяется по формуле:
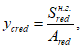 (4.125)
(4.125)
где
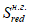 - приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
- приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
A
red
- приведенная площадь полного сечения, м
2
.
Приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения
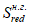 , определяется по формуле:
, определяется по формуле:
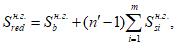 (4.126)
(4.126)
где
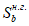 - статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
- статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330;
i
- номер ряда армирования;
m
- количество рядов армирования;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. В таком случае статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения
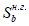 , определяется по формуле:
, определяется по формуле:
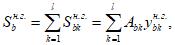 (4.127)
(4.127)
где
k
- номер участка сечения;
l
- количество участков сечения;
A
bk
- площадь
k
-го участка сечения
(рисунок 4.24)
, м
2
;
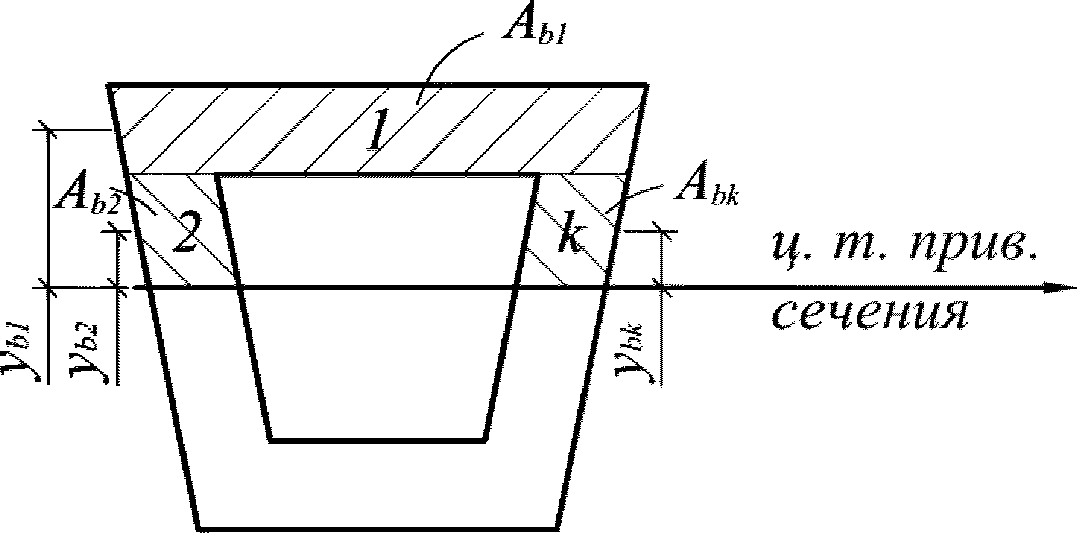
Статический момент инерции
i
-го ряда армирования, взятый относительно нижней грани сечения
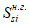 , определяется по формуле:
, определяется по формуле:
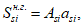 (4.128)
(4.128)
где
A
si
- площадь
i
-го ряда армирования, м
2
;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м.
Приведенная площадь полного сечения
A
red
определяется по формуле:
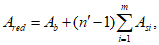 (4.129)
(4.129)
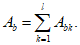 (4.130)
(4.130)
В
формулах (3.41)
-
(3.43)
:
A
b
- площадь бетонной части сечения, м
2
.
Геометрические характеристики сечения изгибаемого элемента определяются без учета работы бетона растянутой зоны.
При
e
cj
> 0 производится расчет геометрических характеристик нормально ориентированного сечения
(рисунок 4.25)
;
При
e
cj
< 0 производится расчет геометрических характеристик обратного сечения (повернутого на 180°)
(рисунок 4.25)
.
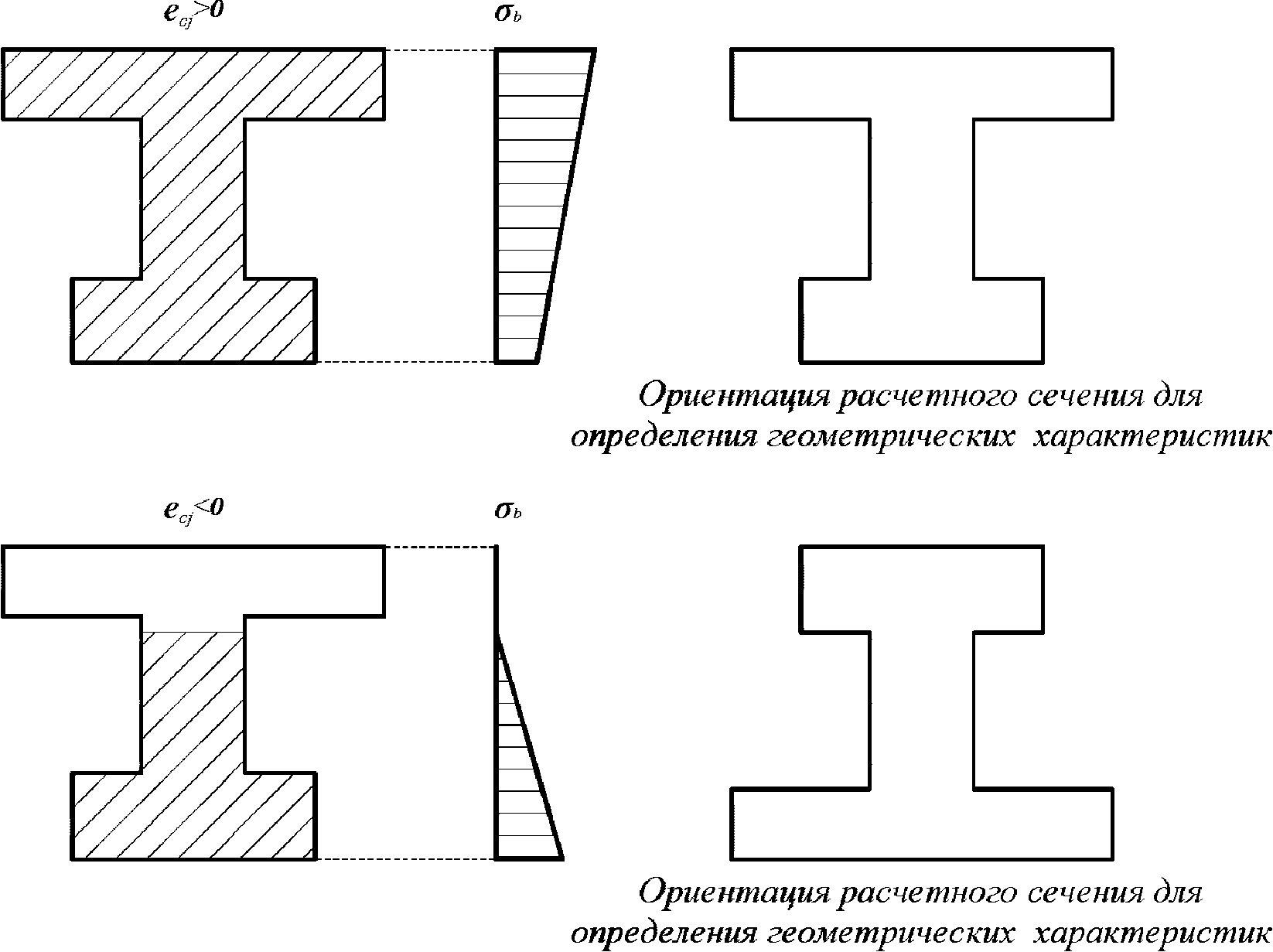
для определения геометрических характеристик
Геометрические характеристики должны быть определены для каждого загружения в отдельности.
Расчет геометрических характеристик сечения для
j
-го загружения заключается в подборе такого расстояния от верхней грани сечения до нейтральной оси
Z
j
, при котором напряжения в уровне нейтральной оси равняются нулю:
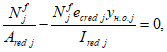 (4.132)
(4.132)
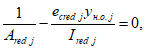 (4.133)
(4.133)
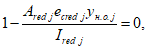 (4.134)
(4.134)
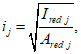 (4.135)
(4.135)
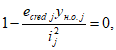 (4.136)
(4.136)
В
формулах (4.131)
-
(4.137)
:
A
red j
- приведенная площадь сечения для
j
-го загружения, м
2
;
y
н.о.j
- расстояние между нейтральной осью и центром тяжести приведенного сечения для
j
-го загружения
(рисунок 4.26)
, м;
I
red j
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения, м
4
;
e
cred j
- эксцентриситет продольной силы
 относительно центра тяжести приведенного сечения для
j
-го загружения
(рисунок 4.26)
, м;
относительно центра тяжести приведенного сечения для
j
-го загружения
(рисунок 4.26)
, м;
i
j
- радиус инерции сечения для
j
-го загружения, м.
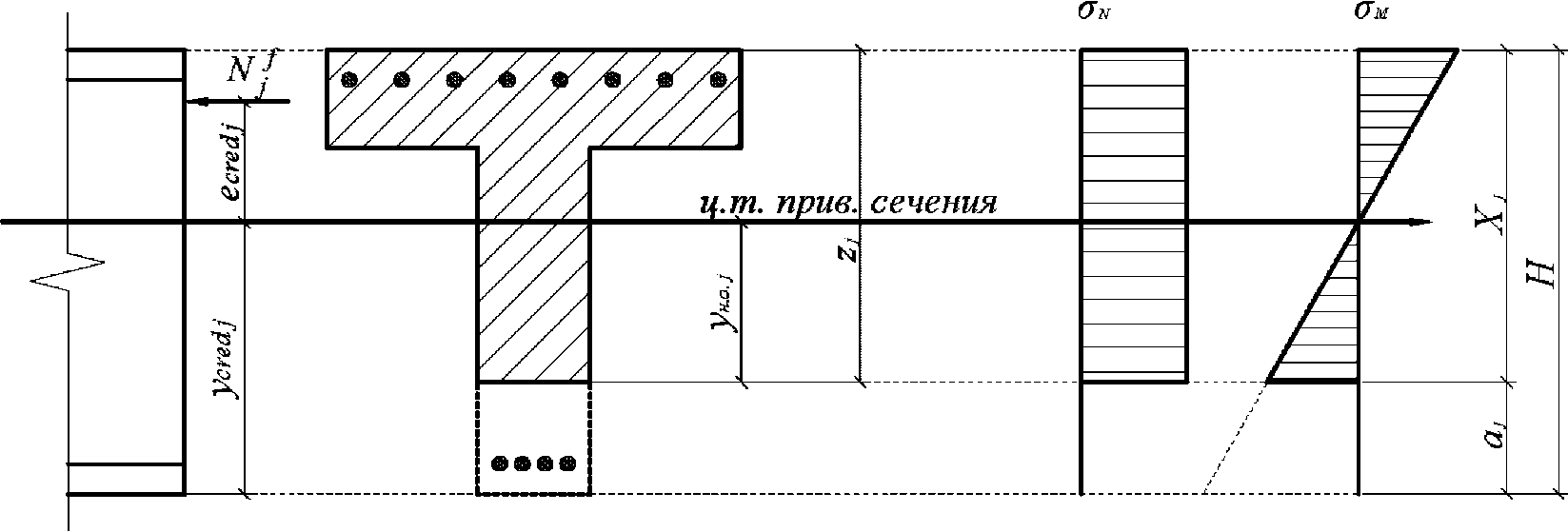
внецентренно сжатого элемента
Эксцентриситет продольной силы
 относительно центра тяжести приведенного сечения для
j
-го загружения
e
cred j
определяется по формуле:
относительно центра тяжести приведенного сечения для
j
-го загружения
e
cred j
определяется по формуле:
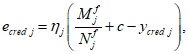 (4.138)
(4.138)
где
 - коэффициент влияния прогиба по прочности для
j
-го загружения;
- коэффициент влияния прогиба по прочности для
j
-го загружения;
c
- расстояние между нижней гранью сечения и осью определения усилий
(рисунок 4.27)
, м;
y
cred j
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения для
j
-го загружения
(рисунок 4.27)
, м.
Расчет
e
cred j
рекомендуется производить при
 , но в случаях, когда деформации системы от действия нагрузок для расчета по выносливости значительно увеличивают усилия в элементе - допускается производить расчет коэффициента влияния прогиба по прочности
, но в случаях, когда деформации системы от действия нагрузок для расчета по выносливости значительно увеличивают усилия в элементе - допускается производить расчет коэффициента влияния прогиба по прочности
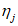 согласно 4.1.5.3. Введение коэффициента влияния прогиба по прочности
согласно 4.1.5.3. Введение коэффициента влияния прогиба по прочности
 существенно увеличивает объем расчетов.
существенно увеличивает объем расчетов.
Расстояние между нейтральной осью и центром тяжести приведенного сечения для
j
-го загружения
y
н.о.j
определяется по формуле:
В
формулах (4.139)
-
(4.140)
:
a
j
- расстояние между нижней гранью сечения и нейтральной осью для
j
-го загружения, м;
H
- высота сечения, м.
При расчете геометрических характеристик необходимо соблюдать следующие условия:
X
j
=
Z
j
; (4.142)
при
Z
j
>
H
, (4.143)
В
формулах (4.141)
-
(4.144)
:
X
j
- высота сжатой зоны бетона для
j
-го загружения, м.
Расстояние между нижней гранью сечения и центром тяжести приведенного сечения для
j
-го загружения
y
cred j
определяется по формуле:
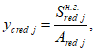 (4.145)
(4.145)
где
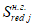 - приведенный статический момент инерции сечения, взятый относительно нижней грани сечения, для
j
-го загружения, м
3
.
- приведенный статический момент инерции сечения, взятый относительно нижней грани сечения, для
j
-го загружения, м
3
.
Приведенный статический момент инерции сечения, взятый относительно нижней грани сечения, для
j
-го загружения
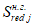 определяется по формуле:
определяется по формуле:
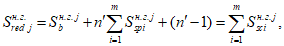 (4.146)
(4.146)
где
 - статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, для
j
-го загружения, м
3
;
- статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, для
j
-го загружения, м
3
;
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330;
i
- номер ряда армирования;
m
- количество рядов армирования;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. В таком случае статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, для
j
-го загружения
 определяется по формуле:
определяется по формуле:
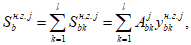 (4.147)
(4.147)
где
k
- номер сжатого участка сечения;
l
- количество участков сечения;
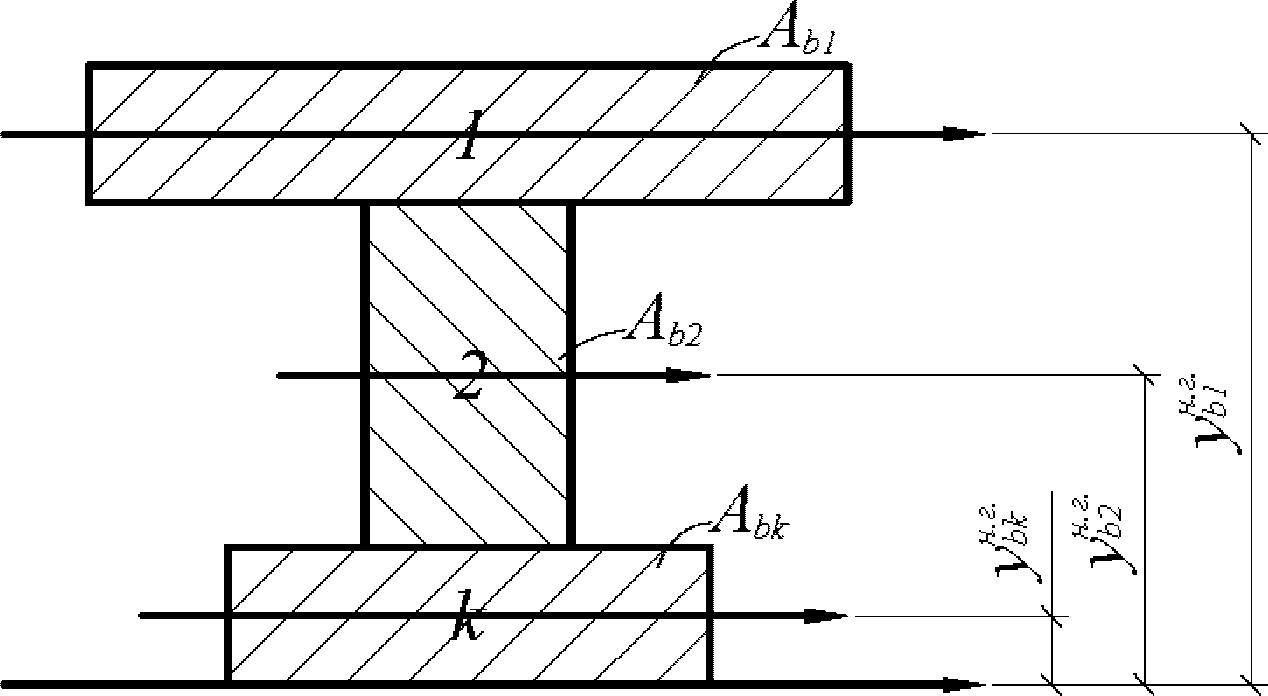
Статический момент инерции
i
-го растянутого ряда армирования, взятый относительно нижней грани сечения, для
j
-го загружения
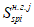 определяется по формуле:
определяется по формуле:
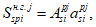 (4.148)
(4.148)
где
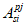 - площадь
i
-го растянутого ряда армирования для
j
-го загружения, м
2
;
- площадь
i
-го растянутого ряда армирования для
j
-го загружения, м
2
;
Статический момент инерции
i
-го сжатого ряда армирования, взятый относительно нижней грани сечения, для
j
-го загружения
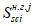 определяется по формуле:
определяется по формуле:
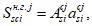 (4.149)
(4.149)
где
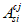 - площадь
i
-го сжатого ряда армирования для
j
-го загружения, м
2
;
- площадь
i
-го сжатого ряда армирования для
j
-го загружения, м
2
;
Для удобства расчетов вводятся следующие критерии, определяющие состояние арматуры:
при
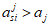 , (4.150)
, (4.150)
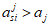 , (4.150)
, (4.150)
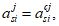 (4.151)
(4.151)
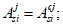 (4.152)
(4.152)
при
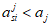 , (4.153)
, (4.153)
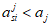 , (4.153)
, (4.153)
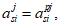 (4.154)
(4.154)
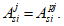 (4.155)
(4.155)
Приведенная площадь сечения
A
red j
определяется по формуле:
В
формулах (4.156)
-
(4.157)
:
A
bj
- площадь сжатой бетонной части сечения для
j
-го загружения, м
2
.
Момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения
I
red j
определяется по формуле:
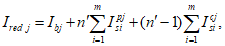 (4.158)
(4.158)
где
I
bj
- момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения, м
4
;
Момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения
I
bj
определяется по формуле:
В
формулах (4.159)
-
(4.160)
:
I
b
0
k
- собственный момент инерции
k
-го сжатого участка сечения для
j
-го загружения, м
4
.
Момент инерции
i
-го растянутого ряда армирования, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения
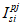 определяется по формуле:
определяется по формуле:
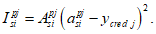 (4.161)
(4.161)
Момент инерции
i
-го сжатого ряда армирования, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения
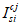 определяется по формуле:
определяется по формуле:
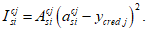 (4.162)
(4.162)
Приведенные выше формулы позволяют вычислить расстояние между верхней гранью элемента и нейтральной осью
Z
j
.
Для железобетонных элементов, имеющих несмещаемые опоры и опоры, одинаково перемещающиеся при вынужденных деформациях (например, при температурных удлинениях), коэффициент влияния прогиба по прочности для
j
-го загружения
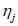 для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
В
формулах (4.163)
-
(4.164)
:
L
- длина рассматриваемого элемента или участка между точками закрепления, м;
L
x
- расстояние от точки закрепления элемента до рассматриваемого сечения, м;
Коэффициент влияния прогиба по прочности для
j
-го загружения
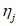 для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
при
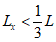 , (4.165)
, (4.165)
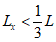 , (4.165)
, (4.165)
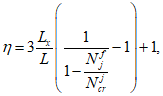 (4.166)
(4.166)
при
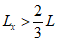 , (4.167)
, (4.167)
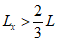 , (4.167)
, (4.167)
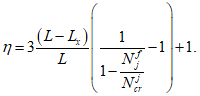 (4.168)
(4.168)
В запас выносливости допускается определять коэффициент влияния прогиба по прочности для
j
-го загружения
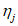 по формуле:
по формуле:
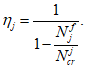 (4.169)
(4.169)
Условная критическая сила железобетонного элемента
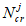 для
j
-го загружения определяется по формуле:
для
j
-го загружения определяется по формуле:
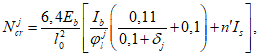 (4.170)
(4.170)
где
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
l
0
- геометрическая длина элемента или ее часть между точками закрепления, принимаемая согласно
п. 7.52
СП 35.13330, м;
I
b
- момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения, м
4
;
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330;
I
s
- момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения, м
4
;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
.
Эксцентриситет продольной силы
 относительно центра тяжести полного приведенного сечения
относительно центра тяжести полного приведенного сечения
 определяется по формуле:
определяется по формуле:
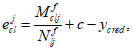 (4.171)
(4.171)
c
- расстояние между нижней гранью сечения и осью определения усилий, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения согласно 4.3.1, м.
Коэффициент, учитывающий влияние на прогиб длительного действия нагрузки для
j
-го загружения
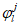 , определяется исходя из условий:
, определяется исходя из условий:
при
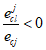 и |
e
cj
| < 0,1
H
, (4.174)
и |
e
cj
| < 0,1
H
, (4.174)
В
формулах (4.172)
-
(4.175)
:
e
cj
- эксцентриситет продольной силы
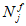 относительно центра тяжести полного приведенного сечения для
j
-го загружения согласно 4.3.1, м;
относительно центра тяжести полного приведенного сечения для
j
-го загружения согласно 4.3.1, м;
H
- высота сечения, м.
Если
 , то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки для
j
-го загружения
, то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки для
j
-го загружения
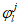 , определяется исходя из условий:
, определяется исходя из условий:
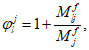 (4.176)
(4.176)
где
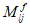 - изгибающий момент от действия постоянных нагрузок для расчета по выносливости, взятый относительно наиболее растянутой или наименее сжатой грани сечения, для
j
-го загружения, кНм;
- изгибающий момент от действия постоянных нагрузок для расчета по выносливости, взятый относительно наиболее растянутой или наименее сжатой грани сечения, для
j
-го загружения, кНм;
Изгибающие моменты от действия постоянных и временных нагрузок для расчета по выносливости и полный изгибающий момент, взятые относительно наиболее растянутой или наименее сжатой грани сечения, определяются по формулам:
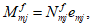 (4.178)
(4.178)
В
формулах (4.177)
-
(4.179)
:
e
lj
- эксцентриситет продольной силы
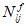 относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м;
относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м;
e
mj
- эксцентриситет продольной силы
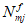 относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м;
относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м;
e
j
- эксцентриситет продольной силы
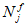 относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м.
относительно наиболее растянутой или наименее сжатой грани сечения для
j
-го загружения
(рисунок 4.29)
, м.

растянутой (наименее сжатой) грани элемента
Эксцентриситеты продольных сил относительно наиболее растянутой или наименее сжатой грани сечения вычисляются по формулам:
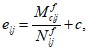 (4.181)
(4.181)
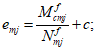 (4.182)
(4.182)
при
e
cj
< 0, (4.183)
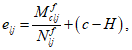 (4.184)
(4.184)
В
формулах (4.180)
-
(4.185)
:
Эксцентриситет продольной силы
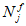 относительно наиболее растянутой или наименее сжатой грани сечения
e
j
определяется по формуле:
относительно наиболее растянутой или наименее сжатой грани сечения
e
j
определяется по формуле:
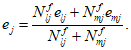 (4.186)
(4.186)
Коэффициент для
j
-го загружения
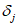 определяется по формуле:
определяется по формуле:
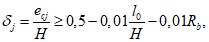 (4.187)
(4.187)
где
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330 (в формулу подставляется в МПа).
В выше приведенных формулах моменты со знаком "+" растягивают нижнюю грань элемента и сжимают верхнюю. Моменты со знаком "-" растягивают верхнюю грань элемента и сжимают нижнюю.
Эксцентриситет со знаком "+" указывает на расположение продольной силы выше центра тяжести полного приведенного сечения. Эксцентриситет со знаком "-" указывает на расположение продольной силы ниже центра тяжести полного приведенного сечения.
Момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения
I
b
, определяется по формуле:
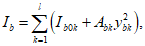 (4.188)
(4.188)
где
I
b
0
k
- собственный момент инерции
k
-го участка сечения, м
4
;
A
bk
- площадь
k
-го участка сечения согласно 4.3.1, м
2
;
y
bk
- расстояние между центром тяжести
k
-го участка и центром тяжести полного приведенного сечения, м.
Момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения
I
s
, определяется по формуле:
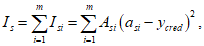 (4.189)
(4.189)
где
i
- номер ряда армирования;
m
- количество рядов армирования;
I
si
- момент инерции
i
-го ряда армирования, взятый относительно центра тяжести полного приведенного сечения, м
4
;
A
si
- площадь
i
-го ряда армирования, м
2
;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м.
Напряжения в бетоне и арматуре определяются по правилам расчета упругих материалов.
Напряжения в бетоне со знаком "+" - сжатие бетона. Бетон на растяжение не работает, поэтому напряжения ограничиваются значениями от нуля и далее.
Напряжения в арматуре со знаком "+" - растяжение армирования, а со знаком "-" - сжатие армирования.
Напряжения в бетоне по верхней
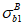 и нижней грани
и нижней грани
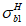 сечения для 1-го загружения определяются по формулам:
сечения для 1-го загружения определяются по формулам:
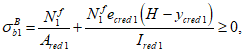 (4.191)
(4.191)
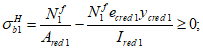 (4.192)
(4.192)
при
e
c
1
< 0, (4.193)
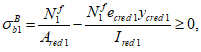 (4.194)
(4.194)
В
формулах (4.190)
-
(4.195)
:
e
c
1
- эксцентриситет продольной силы
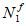 относительно центра тяжести полного приведенного сечения для 1-го загружения согласно 4.1.4.1, м;
относительно центра тяжести полного приведенного сечения для 1-го загружения согласно 4.1.4.1, м;
A
red
1
- приведенная площадь сечения для 1-го загружения согласно 4.1.4.2, м
2
;
e
cred
1
- эксцентриситет продольной силы
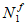 относительно центра тяжести приведенного сечения для 1-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
относительно центра тяжести приведенного сечения для 1-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
H
- высота сечения
(рисунок 4.30)
, м;
y
cred
1
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения для 1-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
I
red
1
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, для 1-го загружения, м
4
;
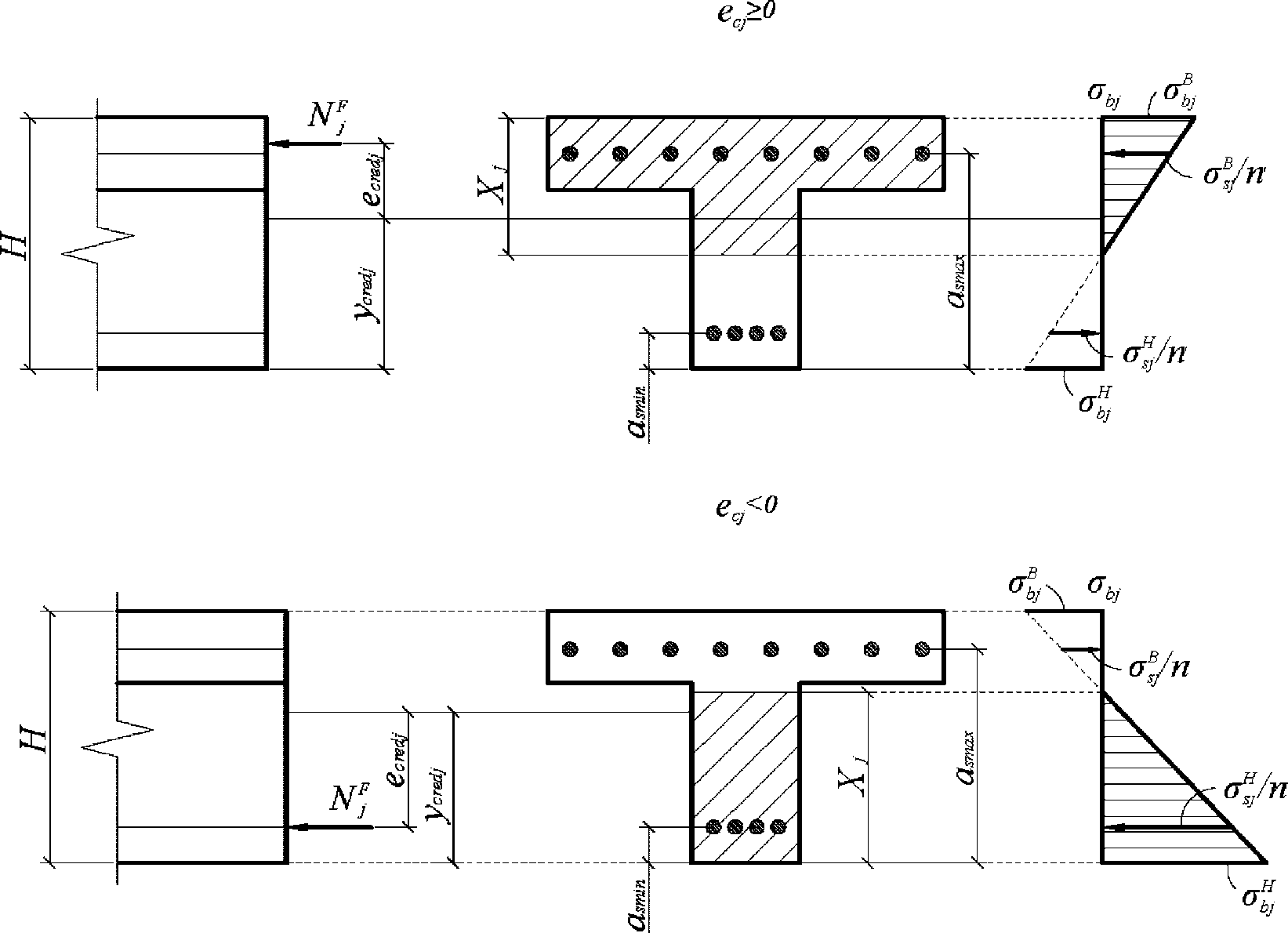
Напряжения в бетоне по верхней
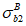 и нижней грани
и нижней грани
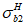 сечения для 2-го загружения определяются по формулам:
сечения для 2-го загружения определяются по формулам:
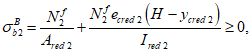 (4.197)
(4.197)
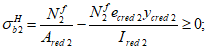 (4.198)
(4.198)
при
e
c
2
< 0, (4.199)
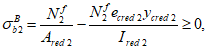 (4.200)
(4.200)
В
формулах (4.196)
-
(3.201)
:
e
c
2
- эксцентриситет продольной силы
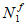 относительно центра тяжести полного приведенного сечения для 2-го загружения согласно 4.1.4.1, м;
относительно центра тяжести полного приведенного сечения для 2-го загружения согласно 4.1.4.1, м;
A
red
2
- приведенная площадь сечения для 2-го загружения согласно 4.1.4.2, м
2
;
e
cred
2
-
эксцентриситет продольной силы
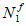 относительно центра тяжести приведенного сечения для 2-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
относительно центра тяжести приведенного сечения для 2-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
y
cred
2
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения для 2-го загружения согласно 4.1.4.2
(рисунок 4.30)
, м;
I
red
2
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, для 2-го загружения, м
4
;
Напряжения в верхнем
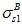 и нижнем ряду армирования
и нижнем ряду армирования
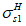 для 1-го загружения определяются по формулам:
для 1-го загружения определяются по формулам:
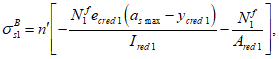 (4.203)
(4.203)
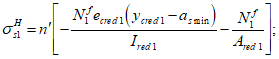 (4.204)
(4.204)
при
e
c
1
< 0
,
(4.205)
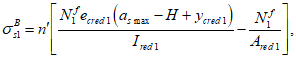 (4.206)
(4.206)
В
формулах (4.202)
-
(4.207)
:
n'
- коэффициент приведения армирования к бетону, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330;
a
s
max
- расстояние между нижней гранью сечения и центром тяжести верхнего ряда армирования
(рисунок 4.30)
, м;
a
s
min
- расстояние между нижней гранью сечения и центром тяжести нижнего ряда армирования
(рисунок 4.30)
, м.
Напряжения в верхнем
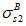 и нижнем ряду армирования
и нижнем ряду армирования
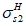 для 2-го загружения определяются по формулам:
для 2-го загружения определяются по формулам:
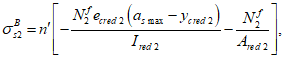 (4.209)
(4.209)
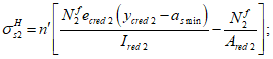 (4.210)
(4.210)
при
e
c
2
< 0, (4.211)
 (4.212)
(4.212)
В
формулах (4.208)
-
(4.213)
:
Проверка выносливости по бетону верхней грани сечения не требуется при условии, что:
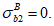 (4.214)
(4.214)
В противном случае производятся следующие расчеты:
Коэффициент асимметрии цикла повторяющихся напряжений для бетона верхней грани сечения
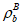 определяется по формуле:
определяется по формуле:
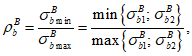 (4.215)
(4.215)
Расчетное сопротивление бетона верхней грани сечения сжатию при расчетах по выносливости
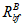 определяется по формуле:
определяется по формуле:
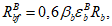 (4.216)
(4.216)
где
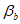 - коэффициент, учитывающий рост прочности бетона во времени и принимаемый по
таблице 7.8
СП 35.13330;
- коэффициент, учитывающий рост прочности бетона во времени и принимаемый по
таблице 7.8
СП 35.13330;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
.
Проверка выносливости по бетону верхней грани сечения заключается в выполнении условия:
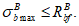 (4.217)
(4.217)
Проверка выносливости по бетону нижней грани сечения не требуется при условии, что:
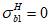 и
и
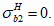 (4.218)
(4.218)
В противном случае производятся следующие расчеты:
Коэффициент асимметрии цикла повторяющихся напряжений для бетона нижней грани сечения
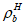 определяется по формуле:
определяется по формуле:
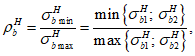 (4.219)
(4.219)
Расчетное сопротивление бетона нижней грани сечения сжатию при расчетах по выносливости
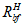 определяется по формуле:
определяется по формуле:
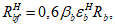 (4.220)
(4.220)
Проверка выносливости по бетону нижней грани сечения заключается в выполнении условия:
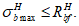 (4.221)
(4.221)
Проверка выносливости верхнего арматурного ряда не требуется при условии, что:
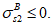 (4.222)
(4.222)
В противном случае производятся следующие расчеты:
Коэффициент асимметрии цикла повторяющихся напряжений для верхнего арматурного ряда
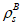 определяется по формуле:
определяется по формуле:
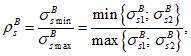 (4.223)
(4.223)
Расчетное сопротивление арматурной стали верхнего ряда армирования при расчетах по выносливости
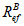 определяется по формуле:
определяется по формуле:
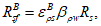 (4.224)
(4.224)
 )
;
)
;
R
s
- расчетное сопротивление арматуры растяжению согласно
таблице 7.16
СП 35.13330, кН/м
2
.
Проверка выносливости верхнего арматурного ряда заключается в выполнении условия:
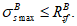 (4.225)
(4.225)
Проверка выносливости нижнего арматурного ряда не требуется при условии, что:
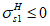 и
и
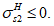 (4.226)
(4.226)
В противном случае производятся следующие расчеты:
Коэффициент асимметрии цикла повторяющихся напряжений для нижнего арматурного ряда
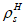 определяется по формуле:
определяется по формуле:
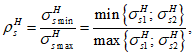 (4.227)
(4.227)
Расчетное сопротивление арматурной стали верхнего ряда армирования при расчетах по выносливости
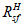 определяется по формуле:
определяется по формуле:
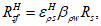 (4.228)
(4.228)
Проверка выносливости нижнего арматурного ряда заключается в выполнении условия:
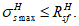 (4.229)
(4.229)
Выше представленный подход к расчету по выносливости обоснован тем, что заранее сложно предугадать какая грань сечения определяет выносливость элемента по бетону и какой ряд армирования определяет выносливость элемента по арматуре.
Сжатые железобетонные элементы должны иметь характеристики, при которых обеспечивается условие:
N
I
<= 0,7
N
cr
, (4.230)
где
N
I
- продольное сжимающее усилие от расчетных нагрузок, кН;
N
cr
- условная критическая сила для железобетонного элемента согласно
4.1.3.2
, кН.
К расчетам по второй группе предельных состояний относятся расчеты по образованию трещин, расчет по ограничению напряжений в растянутой арматуре и расчет ширины раскрытия нормальных трещин
(рисунок 4.31)
.
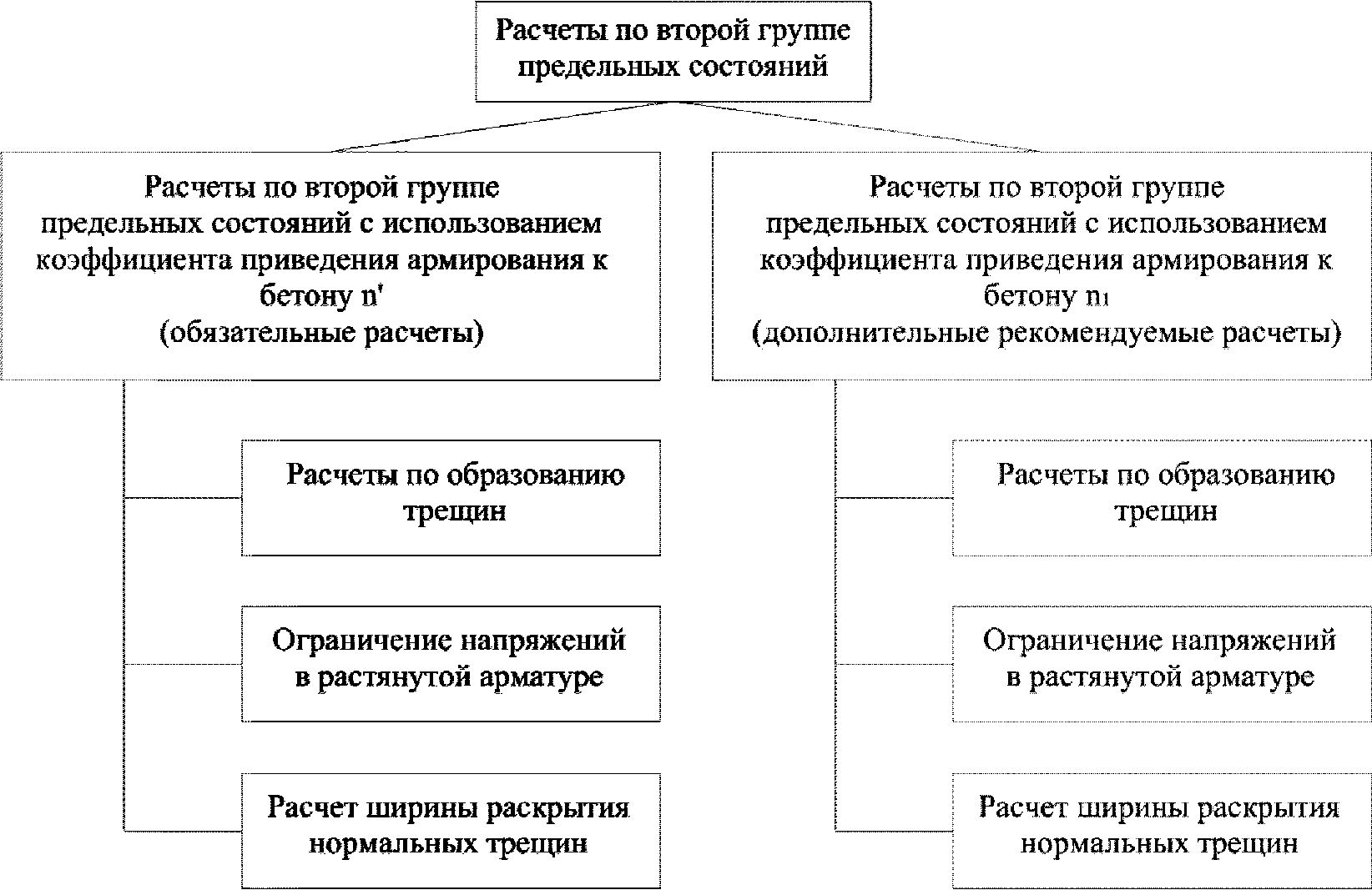
Согласно требованиям
п. 7.48
СП 35.13330 для расчетов на трещиностойкость (для расчета напряжений и геометрических характеристик) используется коэффициент приведения армирования к бетону, учитывающий влияние виброползучести бетона
n'
.
Виброползучесть бетона - это длительный процесс, а усилия, на которые производится расчет по второй группе предельных состояний, возникают и на ранних стадиях эксплуатации конструкции. Поэтому авторы данного пособия также рекомендуют производить все проверки по второй группе предельных состояний с расчетом напряжений и геометрических характеристик сечения при коэффициенте приведения армирования к бетону
n
1
:
В
формулах (4.231)
-
(4.232)
:
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
.
Расчет по образованию продольных трещин заключается в ограничении нормальных сжимающих напряжений в бетоне. Для расчета напряжений предварительно необходимо вычислить геометрические характеристики сечения. Геометрические характеристики сечения определяются без учета работы бетона растянутой зоны
(рисунок 4.32)
.
┌─────────────────────────────┐
│Расчеты по образованию трещин│
└──────────────┬──────────────┘
┌─────────────────┴────────────────┐
│Анализ напряженно-деформированного│
│ состояния сечения │
└─────────────────┬────────────────┘
┌─────────────────┴─────────────────┐
│Расчет коэффициента влияния прогиба│
│ по прочности (не обязательно) │
└─────────────────┬─────────────────┘
┌───────────────────┴───────────────────┐
│Расчет геометрических характеристик при│
│ расчетах по второй группе предельных │
│ состояний │
└───────────────────┬───────────────────┘
┌──────────────┴─────────────┐
│Расчет по образованию трещин│
└────────────────────────────┘
Анализ напряженно-деформированного состояния сечения заключается в определении состояния верхней и нижней граней сечения.
При
e
c
> 0 верхняя грань сечения является наиболее сжатой, а нижняя растянутой или наименее сжатой. В таком случае к расчету геометрических характеристик принимается нормально ориентированное сечение
(рисунок 4.33)
.
При
e
c
< 0 нижняя грань сечения является наиболее сжатой, а верхняя растянутой или наименее сжатой. В таком случае к расчету геометрических характеристик принимается обратное сечение (повернутое на 180°)
(рисунок 4.33)
.
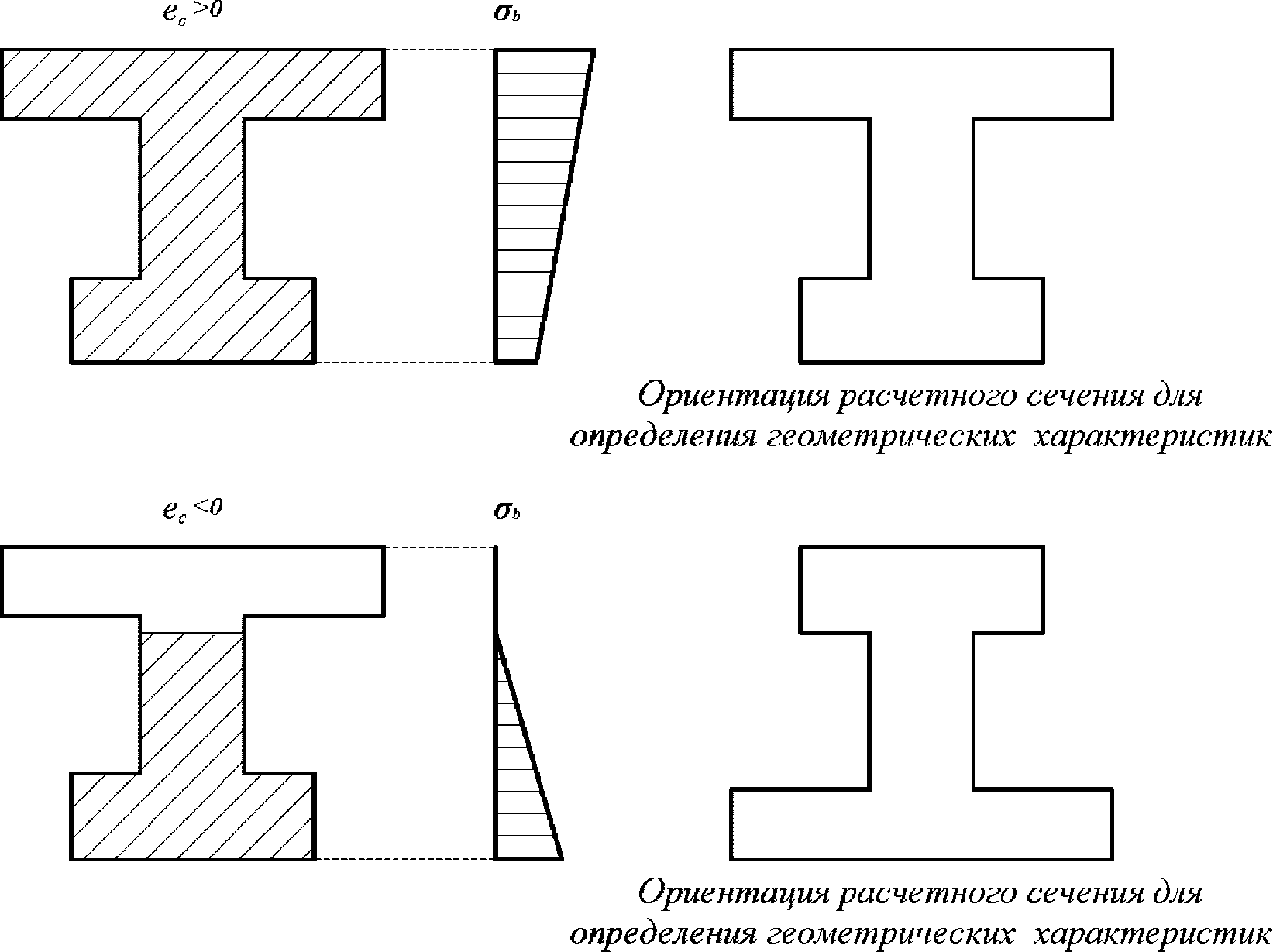
для определения геометрических характеристик;
e
c
- эксцентриситет продольной силы
N
II
относительно
центра тяжести полного приведенного сечения, м
Для удобства расчета вводится понятие "ось определения усилий". Ось определения усилий - это такая ось, относительно которой производится сбор усилий. Такое допущение необходимо в связи с тем, что часто проектировщик не может заранее знать положение центра тяжести приведенного сечения (особенно для сложных, несимметричных сечений). Параметры
n
II
и
M
II
рассчитываются относительно оси определения усилий.
Эксцентриситет продольной силы
N
II
относительно центра тяжести полного приведенного сечения
e
c
вычисляется по формуле:
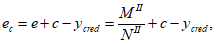 (4.233)
(4.233)
где
N
II
- продольное сжимающее усилие от нормативных нагрузок
(рисунок 4.34)
, кН;
e
- эксцентриситет продольной силы
N
II
относительно оси определения усилий
(рисунок 4.34)
, м;
c
- расстояние между нижней гранью сечения и осью определения усилий
(рисунок 4.34)
, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
(рисунок 4.34)
, м;
M
II
= N
II
e
- изгибающий момент от действия нормативных нагрузок, кНм.

относительно центра тяжести полного приведенного сечения
Расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения
y
cred
определяется по формуле:
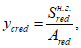 (4.234)
(4.234)
где
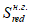 - приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
- приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения, м
3
;
A
red
- приведенная площадь полного сечения, м
2
.
Приведенный статический момент инерции полного сечения, взятый относительно нижней грани сечения
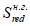 , определяется по формуле:
, определяется по формуле:
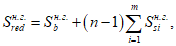 (4.235)
(4.235)
где
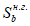 - статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
- статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
n
- коэффициент приведения армирования к бетону согласно
4.2.1
;
i
- номер ряда армирования;
m
- количество рядов армирования;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. В таком случае статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения
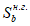 , определяется по формуле:
, определяется по формуле:
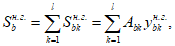 (4.236)
(4.236)
где
k
- номер участка сечения;
l
- количество участков сечения;
A
bk
- площадь
k
-го участка сечения
(рисунок 4.35)
, м
2
;
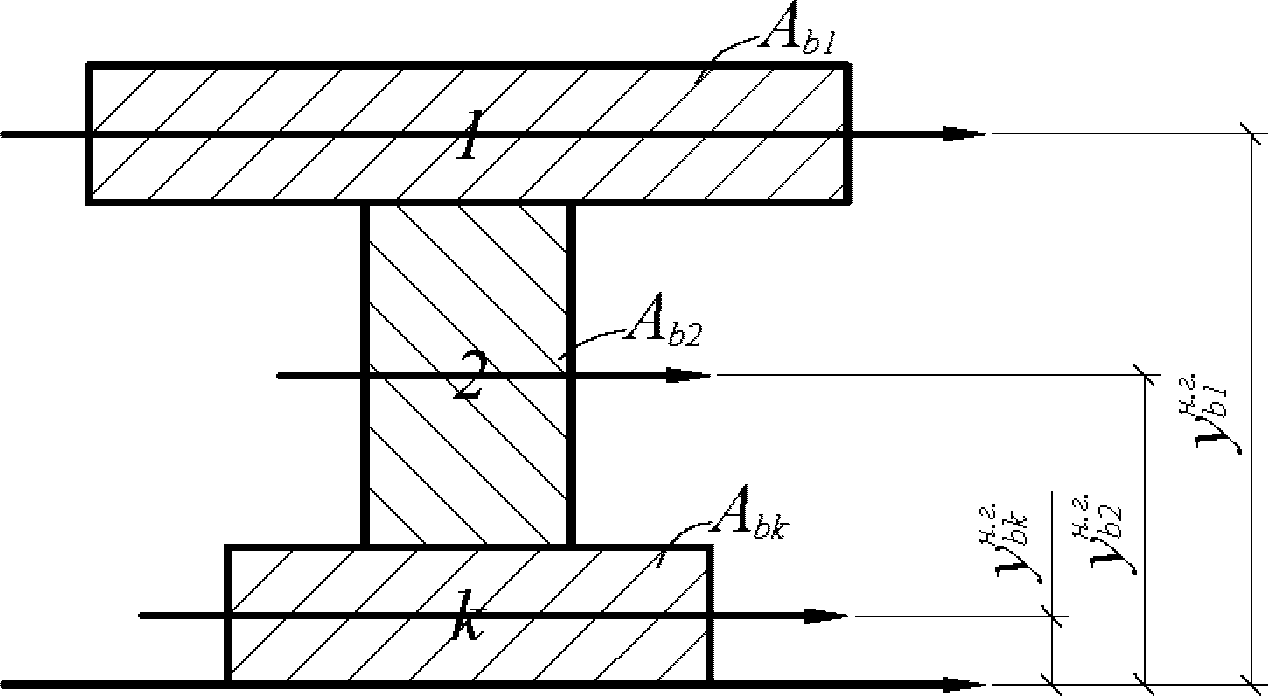
Статический момент инерции
i
-го ряда армирования, взятый относительно нижней грани сечения
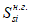 , определяется по формуле:
, определяется по формуле:
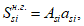 (4.237)
(4.237)
где
A
si
- площадь
i
-го ряда армирования, м
2
;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м.
Приведенная площадь полного сечения
A
red
определяется по формуле:
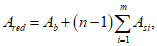 (4.238)
(4.238)
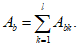 (4.239)
(4.239)
В
формулах (3.41)
-
(3.43)
:
A
b
- площадь бетонной части сечения, м
2
.
Геометрические характеристики сечения изгибаемого элемента определяются без учета работы бетона растянутой зоны.
При
e
c
> 0 производится расчет геометрических характеристик нормально ориентированного сечения
(рисунок 4.36)
.
При
e
c
< 0 производится расчет геометрических характеристик обратного сечения (повернутого на 180°)
(рисунок 4.36)
.
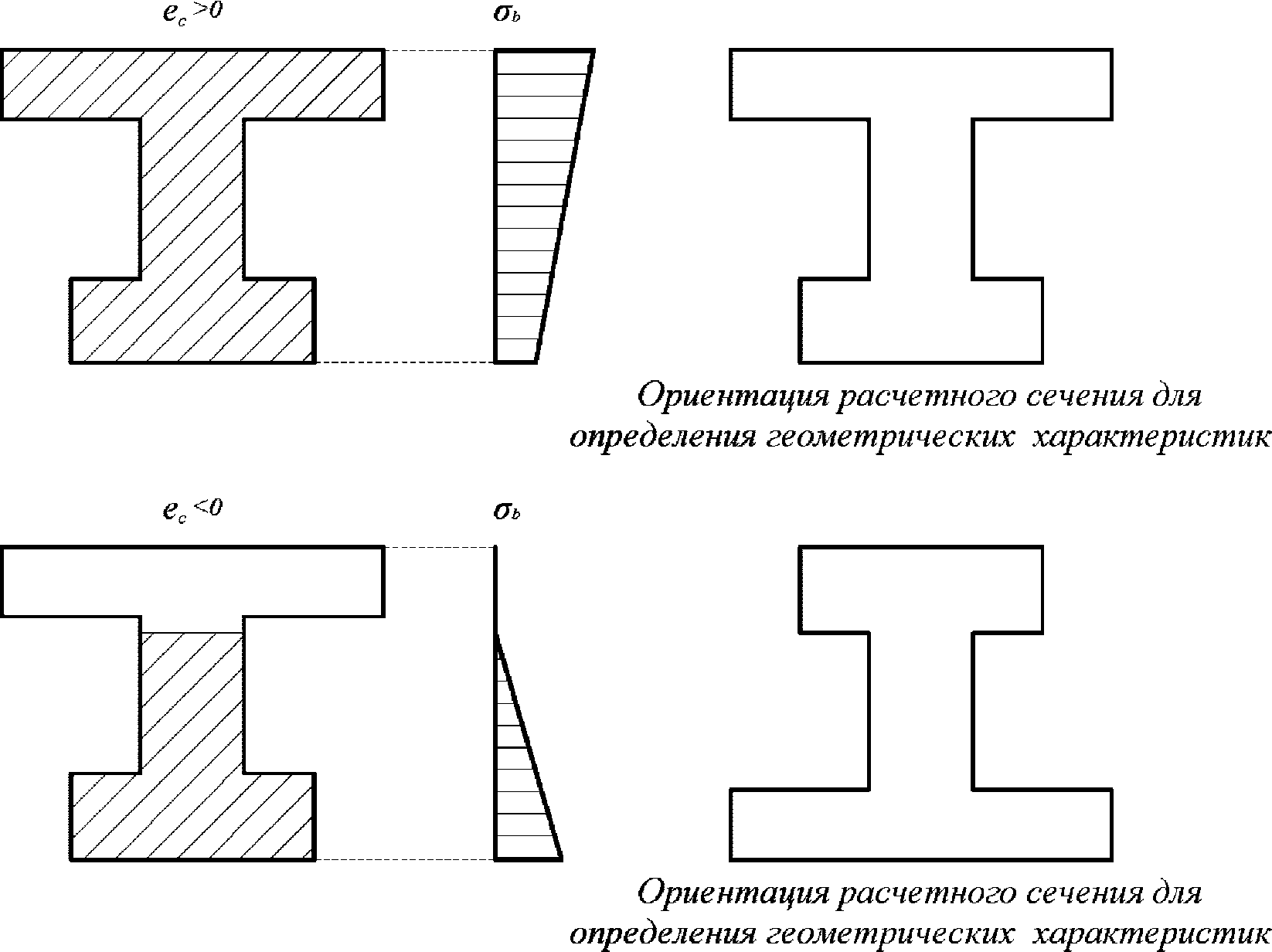
для определения геометрических характеристик
Расчет геометрических характеристик сечения заключается в подборе такого расстояния от верхней грани сечения до нейтральной оси
Z
, при котором напряжения в уровне нейтральной оси равняются нулю:
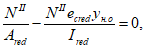 (4.241)
(4.241)
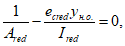 (4.242)
(4.242)
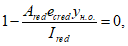 (4.243)
(4.243)
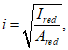 (4.244)
(4.244)
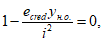 (4.245)
(4.245)
В
формулах (4.240)
-
(4.246)
:
N
II
- продольное сжимающее усилие от нормативных нагрузок
(рисунок 4.37)
, кН;
A
red
- приведенная площадь сечения, м
2
;
M
II
- изгибающий момент от действия нормативных нагрузок, взятый относительно оси определения усилий, кНм;
y
н.о.
- расстояние между нейтральной осью и центром тяжести приведенного сечения
(рисунок 4.37)
, м;
I
red
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, м
4
;
e
cred
- эксцентриситет продольной силы
N
II
относительно центра тяжести приведенного сечения
(рисунок 4.37)
, м;
i
- радиус инерции сечения, м.
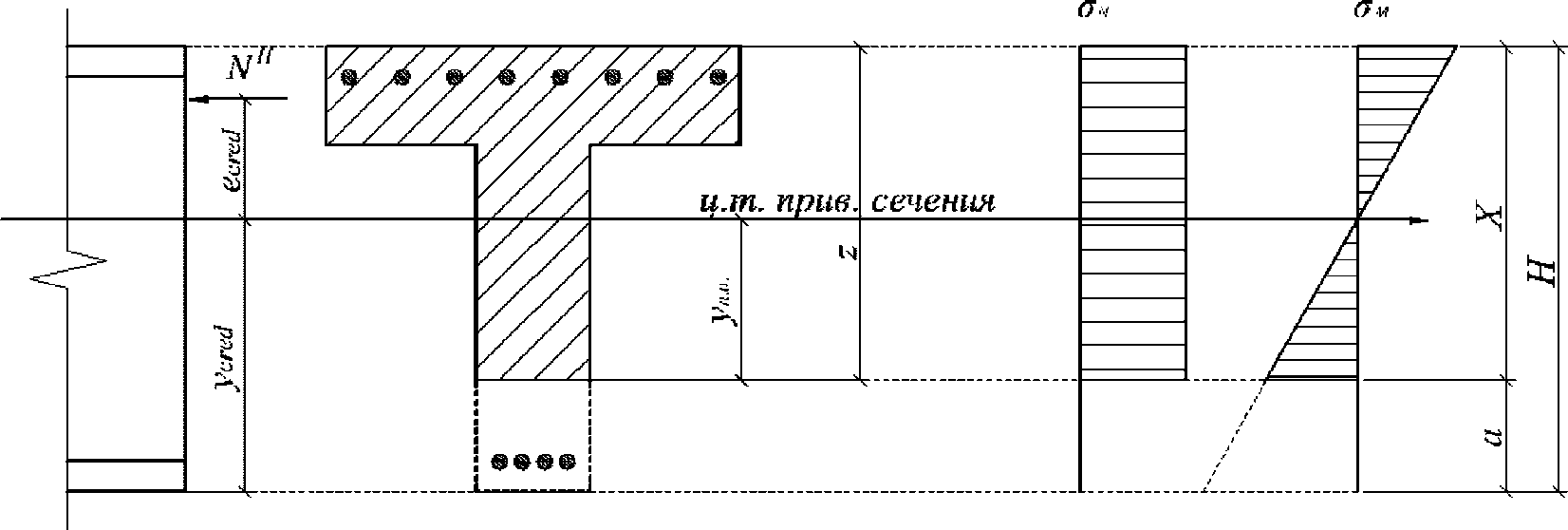
характеристик внецентренно сжатого элемента
Эксцентриситет продольной силы
N
II
относительно центра тяжести приведенного сечения
e
cred
определяется по формуле:
 (4.247)
(4.247)
где
 - коэффициент влияния прогиба по прочности;
- коэффициент влияния прогиба по прочности;
c
- расстояние между нижней гранью сечения и осью определения усилий, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения, м.
Расчет
e
cred
рекомендуется производить при
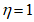 , но в случаях, когда деформации системы от действия нормативных нагрузок значительно увеличивают усилия в элементе - допускается производить расчет коэффициента влияния прогиба по прочности
, но в случаях, когда деформации системы от действия нормативных нагрузок значительно увеличивают усилия в элементе - допускается производить расчет коэффициента влияния прогиба по прочности
 согласно
4.2.1.3
.
согласно
4.2.1.3
.
Расстояние между нейтральной осью и центром тяжести приведенного сечения для
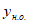 определяется по формуле:
определяется по формуле:
В
формулах (4.248)
-
(4.249)
:
a
- расстояние между нижней гранью сечения и нейтральной осью, м;
H
- высота сечения, м.
При расчете геометрических характеристик необходимо соблюдать следующие условия:
X
=
Z
; (4.251)
при
Z
>
H
, (4.252)
В
формулах (4.250)
-
(4.253)
:
X
- высота сжатой зоны бетона, м.
Расстояние между нижней гранью сечения и центром тяжести приведенного сечения
y
cred
определяется по формуле:
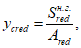 (4.254)
(4.254)
где
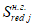 - приведенный статический момент инерции сечения, взятый относительно нижней грани сечения, м
3
.
- приведенный статический момент инерции сечения, взятый относительно нижней грани сечения, м
3
.
Приведенный статический момент инерции сечения, взятый относительно нижней грани сечения
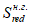 , определяется по формуле:
, определяется по формуле:
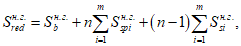 (4.255)
(4.255)
где
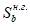 - статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
- статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения, м
3
;
n
- коэффициент приведения армирования к бетону согласно
4.2.1
;
i
- номер ряда армирования;
m
- количество рядов армирования;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. В таком случае статический момент инерции бетонной части сечения, взятый относительно нижней грани сечения
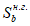 ,
определяется по формуле:
,
определяется по формуле:
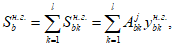 (4.256)
(4.256)
где
k
- номер сжатого участка сечения;
l
- количество участков сечения;
A
bk
- площадь
k
-го сжатого участка сечения
(рисунок 4.38)
, м
2
;
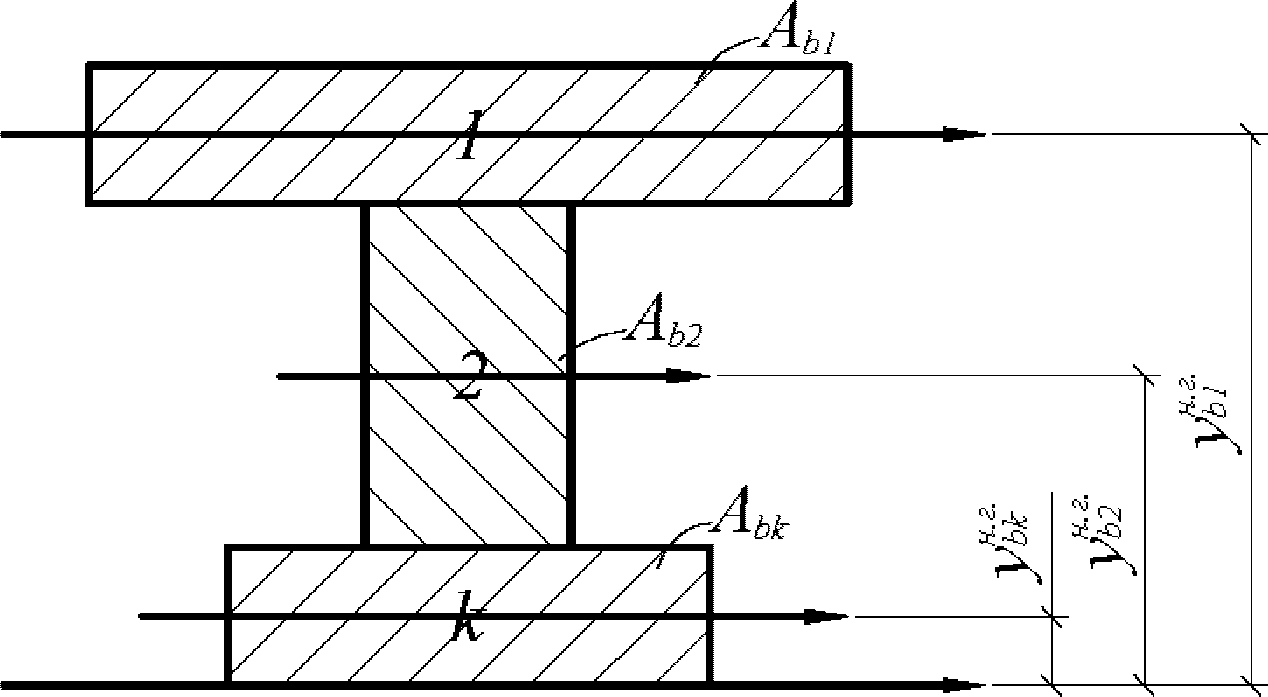
Статический момент инерции
i
-го растянутого ряда армирования, взятый относительно нижней грани сечения
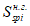 , определяется по формуле:
, определяется по формуле:
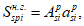 (4.257)
(4.257)
где
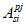 - площадь
i
-го растянутого ряда армирования, м
2
;
- площадь
i
-го растянутого ряда армирования, м
2
;
Статический момент инерции
i
-го сжатого ряда армирования, взятый относительно нижней грани сечения
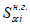 ,
определяется по формуле:
,
определяется по формуле:
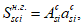 (4.258)
(4.258)
где
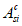 - площадь
i
-го сжатого ряда армирования, м
2
;
- площадь
i
-го сжатого ряда армирования, м
2
;
Для удобства расчетов вводятся следующие критерии, определяющие состояние арматуры:
при
a
si
>
a
, (4.259)
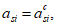 (4.260)
(4.260)
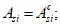 (4.261)
(4.261)
при
a
si
< a
, (4.262)
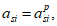 (4.263)
(4.263)
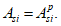 (4.264)
(4.264)
Приведенная площадь сечения
A
red
определяется по формуле:
В
формулах (4.265)
-
(4.266)
:
A
b
- площадь сжатой бетонной части сечения, м
2
.
Момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения
I
red
, определяется по формуле:
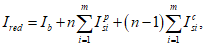 (4.267)
(4.267)
где
I
b
- момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, м
4
;
Момент инерции сжатой бетонной части сечения, взятый относительно центра тяжести приведенного сечения, для
j
-го загружения
I
bj
определяется по формуле:
В
формулах (4.268)
-
(4.269)
:
I
b
0
k
- собственный момент инерции
k
-го сжатого участка сечения, м
4
.
Момент инерции
i
-го растянутого ряда армирования, взятый относительно центра тяжести приведенного сечения
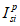 , определяется по формуле:
, определяется по формуле:
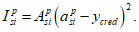 (4.270)
(4.270)
Момент инерции
i
-го сжатого ряда армирования, взятый относительно центра тяжести приведенного сечения
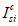 , определяется по формуле:
, определяется по формуле:
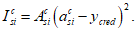 (4.271)
(4.271)
Приведенные выше формулы позволяют вычислить расстояние между верхней гранью элемента и нейтральной осью
Z.
Для железобетонных элементов, имеющих несмещаемые опоры и опоры, одинаково перемещающиеся при вынужденных деформациях (например, при температурных удлинениях), коэффициент влияния прогиба по прочности
 для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в средней трети длины рассматриваемого элемента, определяется по формуле:
при
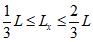 , (4.272)
, (4.272)
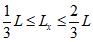 , (4.272)
, (4.272)
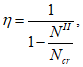 (4.273)
(4.273)
где
L
- длина рассматриваемого элемента или участка между точками закрепления, м;
L
x
- расстояние от точки закрепления элемента до рассматриваемого сечения, м;
N
II
- продольное сжимающее усилие от нормативных нагрузок, кН;
N
cr
- условная критическая сила для железобетонного элемента, кН.
Коэффициент влияния прогиба по прочности
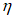 для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
для сечений, лежащих в крайних третях длины рассматриваемого элемента, определяется по формуле:
при
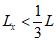 , (4.274)
, (4.274)
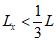 , (4.274)
, (4.274)
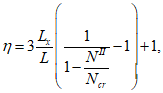 (4.275)
(4.275)
при
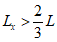 , (4.276)
, (4.276)
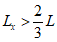 , (4.276)
, (4.276)
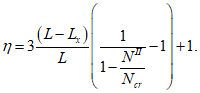 (4.277)
(4.277)
В запас прочности допускается определять коэффициент влияния прогиба по прочности
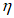 по формуле:
по формуле:
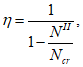 (4.278)
(4.278)
N
II
- продольное сжимающее усилие от нормативных нагрузок, кН;
N
cr
- условная критическая сила для железобетонного элемента, кН.
Условная критическая сила для железобетонного элемента
N
cr
, определяется по формуле:
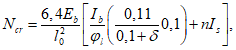 (4.279)
(4.279)
где
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
;
l
0
- геометрическая длина элемента или ее часть между точками закрепления, принимаемая согласно
п. 7.52
СП 35.13330, м;
I
b
- момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения, м
4
;
n
- коэффициент приведения армирования к бетону согласно
4.2.1
;
I
s
- момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения, м
4
;
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
.
Эксцентриситет продольной силы
N
II
относительно центра тяжести полного приведенного сечения
e
cl
определяется по формулам:
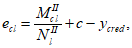 (4.280)
(4.280)
c
- расстояние между нижней гранью сечения и осью определения усилий, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести полного приведенного сечения согласно
4.2.1.1
, м.
Коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
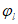 , определяется исходя из условий:
, определяется исходя из условий:
при
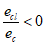 и |
e
c
| < 0,1
H
, (4.283)
и |
e
c
| < 0,1
H
, (4.283)
В
формулах (4.281)
-
(4.284)
:
e
c
- эксцентриситет продольной силы
N
II
относительно центра тяжести полного приведенного сечения согласно
4.2.1.1
, м;
H
- высота сечения, м.
Если
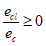 , то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
, то коэффициент, учитывающий влияние на прогиб длительного действия нагрузки
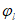 , определяется исходя из условий:
, определяется исходя из условий:
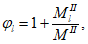 (4.285)
(4.285)
где
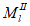 - изгибающий момент от действия постоянных нормативных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм;
- изгибающий момент от действия постоянных нормативных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм;
M
II
- изгибающий момент от действия постоянных и временных нормативных нагрузок, взятый относительно наиболее растянутой или наименее сжатой грани сечения, кНм.
Изгибающие моменты от действия постоянных и временных нормативных нагрузок и полный изгибающий момент, взятые относительно наиболее растянутой или наименее сжатой грани сечения, определяются по формулам:
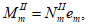 (4.287)
(4.287)
В
формулах (4.286)
-
(4.288)
:
e
l
- эксцентриситет продольной силы
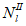 относительно наиболее растянутой или наименее сжатой грани сечения
(рисунок 4.39)
, м;
относительно наиболее растянутой или наименее сжатой грани сечения
(рисунок 4.39)
, м;
e
m
- эксцентриситет продольной силы
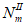 относительно наиболее растянутой или наименее сжатой грани сечения
(рисунок 4.39)
, м;
относительно наиболее растянутой или наименее сжатой грани сечения
(рисунок 4.39)
, м;
e
- эксцентриситет продольной силы
N
II
относительно наиболее растянутой или наименее сжатой грани сечения
(рисунок 4.39)
, м.
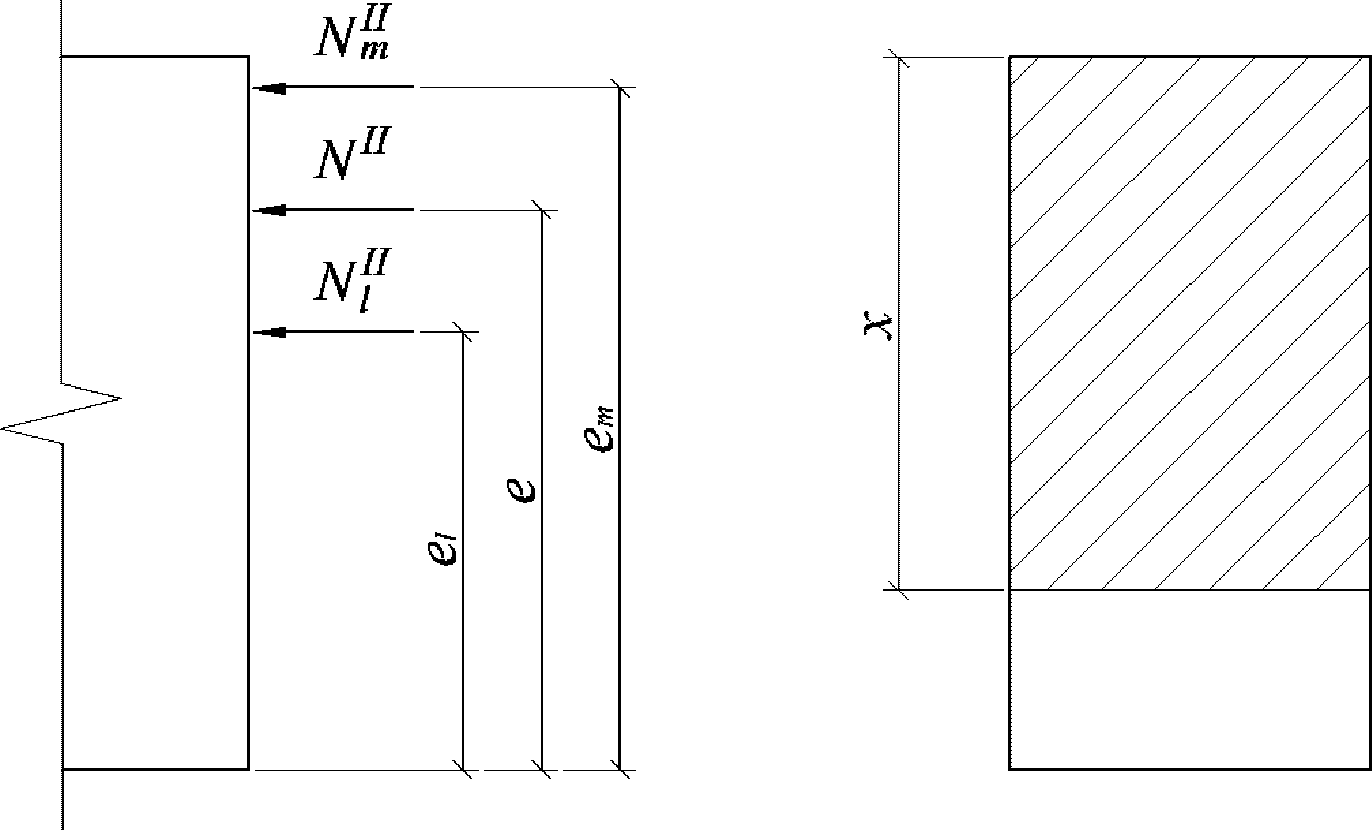
растянутой (наименее сжатой) грани элемента
Эксцентриситеты продольных сил относительно наиболее растянутой или наименее сжатой грани сечения вычисляются по формулам:
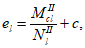 (4.290)
(4.290)
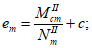 (4.291)
(4.291)
при
e
c
< 0, (4.292)
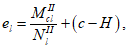 (4.293)
(4.293)
В
формулах (4.289)
-
(4.294)
:
Эксцентриситет продольной силы
N
II
относительно наиболее растянутой или наименее сжатой грани сечения
e
определяется по формуле:
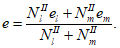 (4.295)
(4.295)
Коэффициент
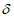 определяется по формуле:
определяется по формуле:
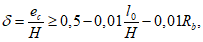 (4.296)
(4.296)
где
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330 (в формулу подставляется в МПа).
В выше приведенных формулах моменты со знаком "+" растягивают нижнюю грань элемента и сжимают верхнюю. Моменты со знаком "-" растягивают верхнюю грань элемента и сжимают нижнюю.
Эксцентриситет со знаком "+" указывает на расположение продольной силы выше центра тяжести полного приведенного сечения. Эксцентриситет со знаком "-" указывает на расположение продольной силы ниже центра тяжести полного приведенного сечения.
Момент инерции бетонной части сечения, взятый относительно центра тяжести полного приведенного сечения
I
b
, определяется по формуле:
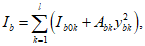 (4.297)
(4.297)
где
I
b
0
k
- собственный момент инерции
k
-го участка сечения, м
4
;
A
bk
- площадь
k
-го участка сечения согласно
4.2.1.1
, м
2
;
y
bk
- расстояние между центром тяжести
k
-го участка и центром тяжести полного приведенного сечения, м.
Момент инерции армирования, взятый относительно центра тяжести полного приведенного сечения
I
s
, определяется по формуле:
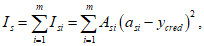 (4.298)
(4.298)
где
i
- номер ряда армирования;
m
- количество рядов армирования;
I
si
- момент инерции
i
-го ряда армирования, взятый относительно центра тяжести полного приведенного сечения, м
4
;
A
si
- площадь
i
-го ряда армирования, м
2
;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м.
Нормальные сжимающие напряжения в бетоне
 определяются по формуле:
определяются по формуле:
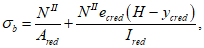 (4.299)
(4.299)
где
N
II
- продольное сжимающее усилие от нормативных нагрузок
(рисунок 4.40)
, кН;
A
red
- приведенная площадь сечения согласно
4.2.1.2
, м
2
;
e
cred
- эксцентриситет продольной силы
N
II
относительно центра тяжести приведенного сечения согласно
4.2.1.2
(рисунок 4.40)
, м;
H
- высота сечения
(рисунок 4.40)
, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения согласно
4.2.1.2
(рисунок 4.40)
, м;
I
red
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения согласно
4.2.1.2
, м
4
.
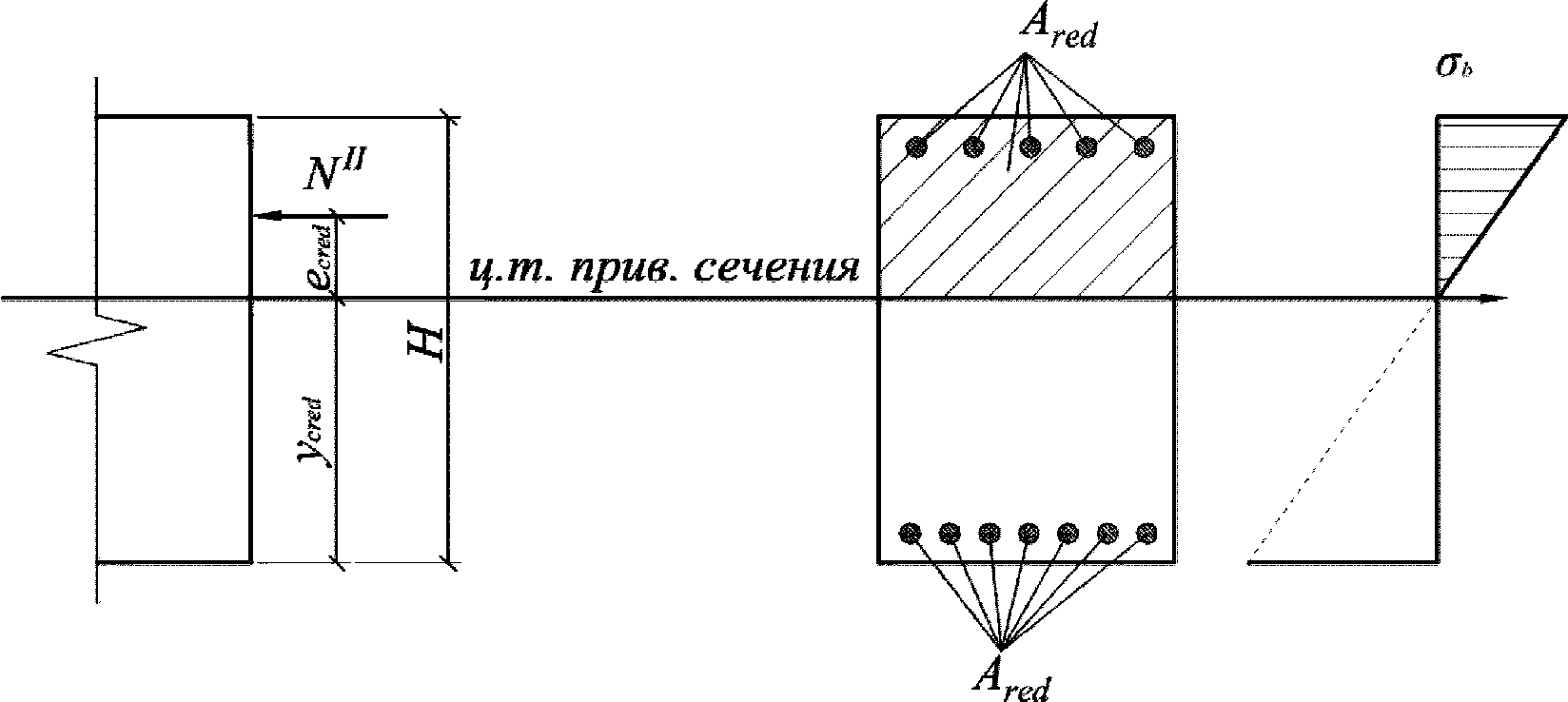
сжимающих напряжений в бетоне
Ограничение нормальных сжимающих напряжений в бетоне
 производится согласно условию:
производится согласно условию:
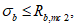 (4.300)
(4.300)
где
R
b,mc
2
- сопротивление бетона осевому сжатию для расчетов по предотвращению образования в конструкциях продольных трещин на стадии эксплуатации согласно
таблице 7.6
СП 35.13330, кН/м
2
.
Нормальные напряжения в наиболее растянутом ряду армирования
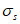 определяются по формулам:
определяются по формулам:
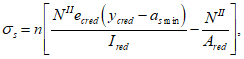 (4.302)
(4.302)
при
e
c
< 0, (4.303)
В
формулах (4.301)
-
(4.304)
:
e
c
- эксцентриситет продольной силы
N
II
относительно центра тяжести полного приведенного сечения согласно
4.2.1.1
(рисунок 4.41)
, м;
n
- коэффициент приведения армирования к бетону согласно
4.2.1
;
N
II
- продольное сжимающее усилие от нормативных нагрузок
(рисунок 4.41)
, кН;
e
cred
- эксцентриситет продольной силы
N
II
относительно центра тяжести приведенного сечения согласно
4.2.1.2
(рисунок 4.41)
, м;
y
cred
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения согласно
4.2.1.2
(рисунок 4.41)
, м;
a
s
min
- расстояние между нижней гранью сечения и центром тяжести нижнего ряда армирования
(рисунок 4.41)
, м;
I
red
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения согласно
4.2.1.2
, м
4
;
A
red
- приведенная площадь сечения согласно
4.2.1.2
, м
2
;
a
s
max
- расстояние между нижней гранью сечения и центром тяжести верхнего ряда армирования
(рисунок 4.41)
, м;
H
- высота сечения
(рисунок 4.41)
, м.
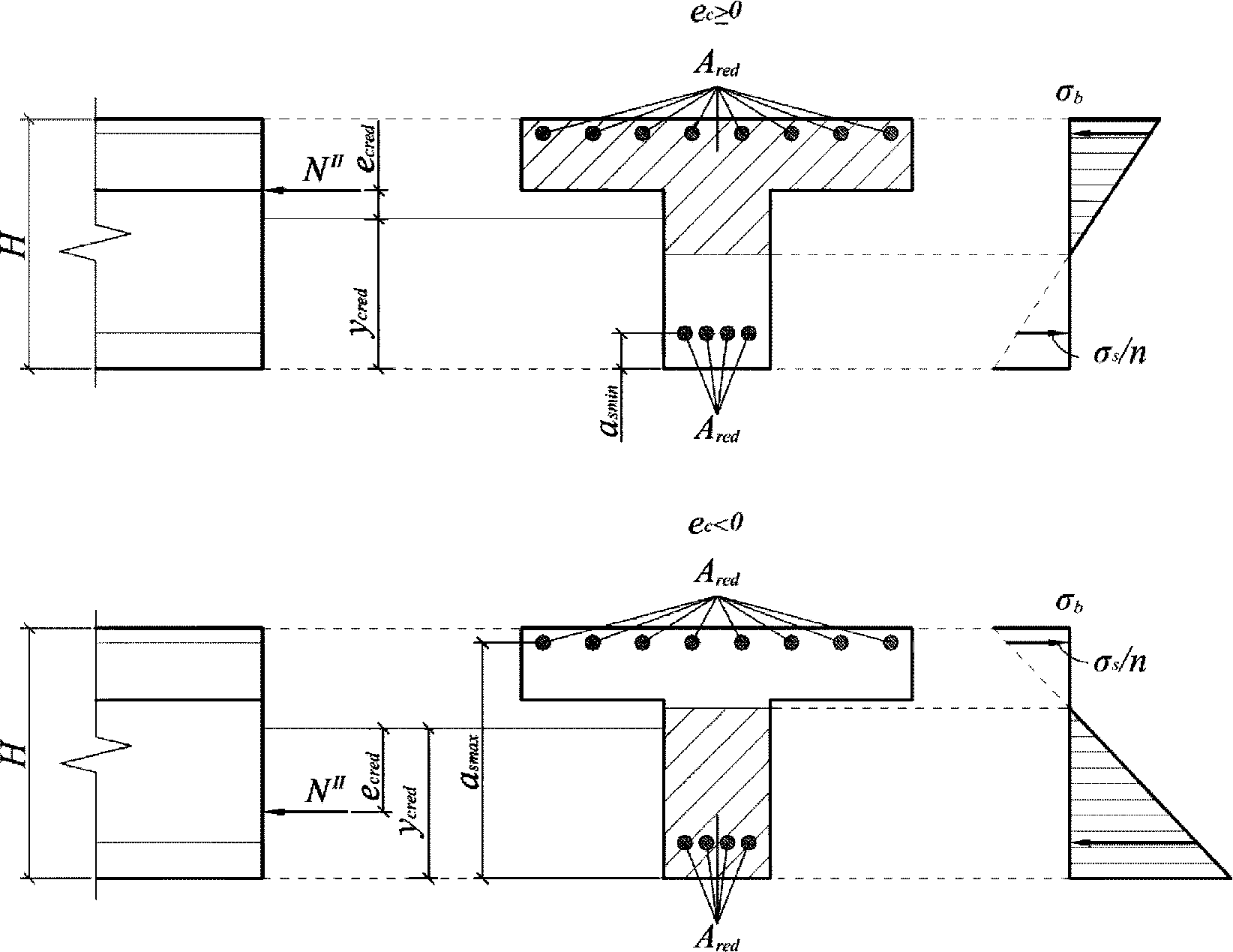
в наиболее растянутом ряду армирования
Ограничение нормальных напряжений в наиболее растянутом ряду армирования
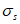 производится согласно условию:
производится согласно условию:
 (4.305)
(4.305)
где
R
sn
- нормативное сопротивление арматуры растяжению согласно
таблицам 7.15
и
7.16
СП 35.13330, кН/м
2
.
Расчет заключается в определении ширины раскрытия нормальных трещин
a
cr
и сравнении ее с предельным значением расчетной ширины раскрытия трещин
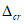 .
.
Расчетная ширина раскрытия нормальных трещин
a
cr
определяется по формуле:
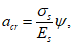 (4.306)
(4.306)
где
 - напряжения в наиболее растянутом ряду армирования согласно
4.2.2
, кН/м
2
;
- напряжения в наиболее растянутом ряду армирования согласно
4.2.2
, кН/м
2
;
E
s
- модуль упругости армирования, кН/м
2
;
Ограничение ширины раскрытия нормальных трещин производится согласно условию:
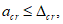 (4.307)
(4.307)
где
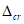 - предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
- предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
Для гладкой стержневой арматуры, арматурных пучков из гладкой проволоки и для стальных закрытых канатов коэффициент раскрытия трещин
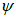 определяется по формуле:
определяется по формуле:
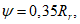 (4.308)
(4.308)
где
R
r
- радиус армирования, см.
Для стержневой арматуры периодического профиля, проволок периодического профиля класса Вр, пучков из этой проволоки, канатов класса К7 и пучков из них, стальных канатов со спиральной и двойной свивкой, а также для любой арматуры в стенках коэффициента раскрытия трещин
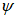 определяется по формуле:
определяется по формуле:
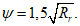 (4.309)
(4.309)
Радиус армирования
R
r
определяется по формуле:
 (4.310)
(4.310)
где
A
r
- площадь зоны взаимодействия для нормального сечения, принимаемая ограниченной наружным контуром сечения и радиусом взаимодействия
r
, которая не должна выходить за пределы растянутой зоны сечения
(рисунок 4.42)
, см
2
;
n
- число арматурных элементов с одинаковым номинальным диаметром
d
;
d
- диаметр одного стержня (включая случаи расположения в группах), см.
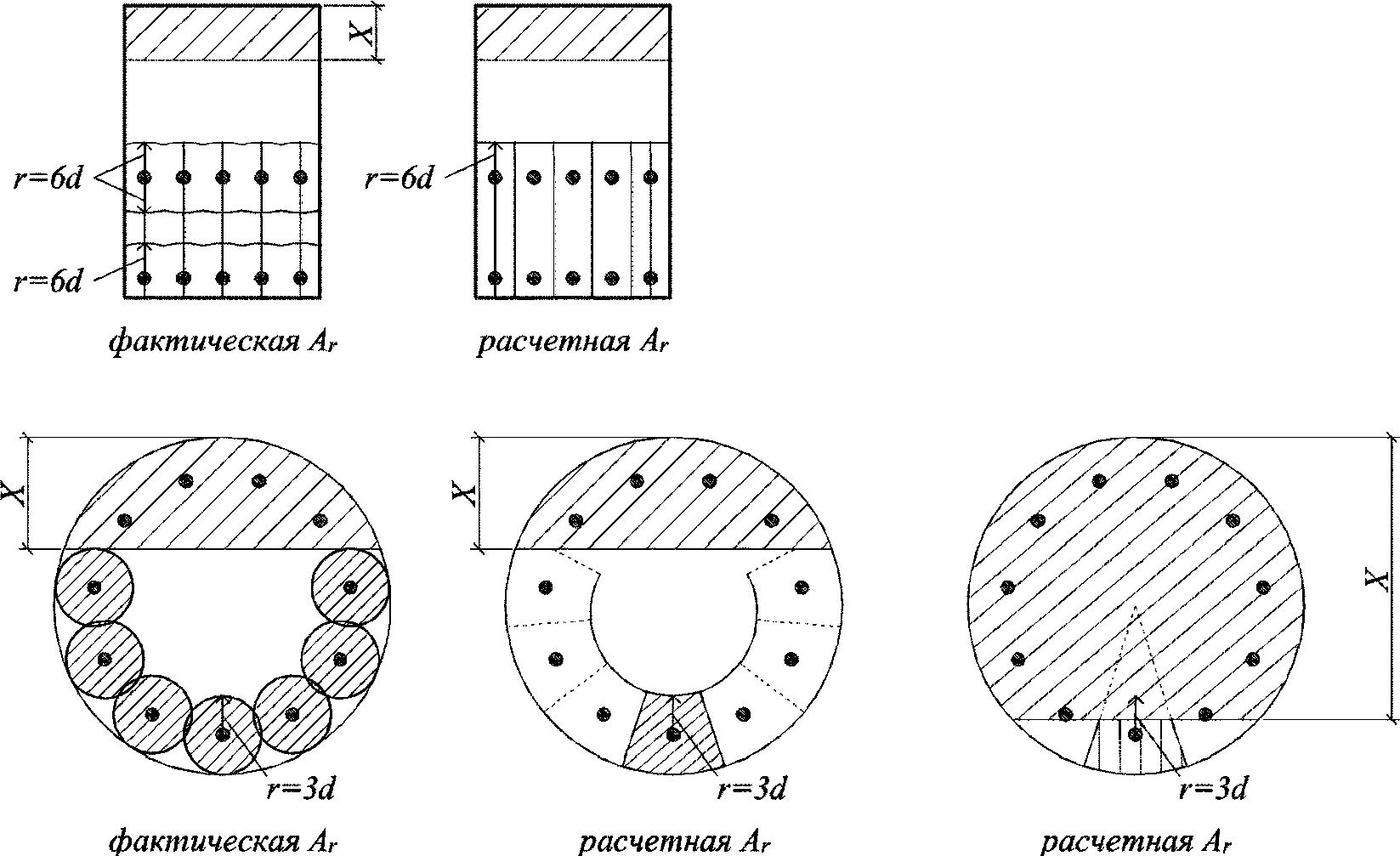
В круглых сечениях площадь зоны взаимодействия
A
r
и радиус армирования
R
r
следует определять для наиболее растянутого стержня или пучка.
Высота растянутой зоны сечения
a
определяется по формуле:
a
=
H
-
X
, (4.311)
где
H
- высота сечения, м;
X
- высота сжатой зоны бетона согласно
4.2.1.2
, м.
Для непрямоугольных сечений с арматурой, равномерно распределенной по контуру, радиус взаимодействия принимается
r
= 3
d.
Для пучков и канатов диаметр
d
соответствует наружному контуру арматурного элемента, а
r
= 5
d.
Во всех остальных случаях
r
= 6
d.
Сумма
 определяется по формуле:
определяется по формуле:
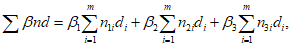 (4.312)
(4.312)
где
 - коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
- коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
n
1
i
- количество одиночных стержней в
i
-ом ряду армирования;
d
i
- диаметр стержней
i
-го ряда армирования, см;
n
2
i
- количество сдвоенных стержней в
i
-ом ряду армирования;
n
3
i
- количество строенных стержней в
i
-ом ряду армирования.
Для внецентренно сжатых элементов возможны случаи, когда все армирование или все сечение сжато и тогда
a
cr
= 0.
Расчеты элементов, подверженных воздействию поперечных сил, делятся на две большие группы: расчеты по первой группе предельных состояний и расчеты по второй группе предельных состояний
(рисунок 5.1)
.
поперечных сил
К расчетам по первой группе предельных состояний относятся проверка прочности по сжатому бетону между наклонными трещинами, расчет наклонных сечений на действие поперечной силы и расчет наклонных трещин на действие изгибающих моментов
(рисунок 5.2)
.
Для железобетонных элементов, подверженных воздействию поперечных сил, должно соблюдаться условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами:
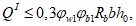 (5.1)
(5.1)
где
Q
I
- поперечная сила от расчетных нагрузок, кН;
R
b
- расчетное сопротивление бетона сжатию согласно
таблице 7.6
СП 35.13330, кН/м
2
;
b
- толщина стенки (ребра) или ширина сплошной плиты, м;
h
0
-
рабочая высота сечения, пересекающего конец наклонной трещины
(рисунок 5.3)
, м.
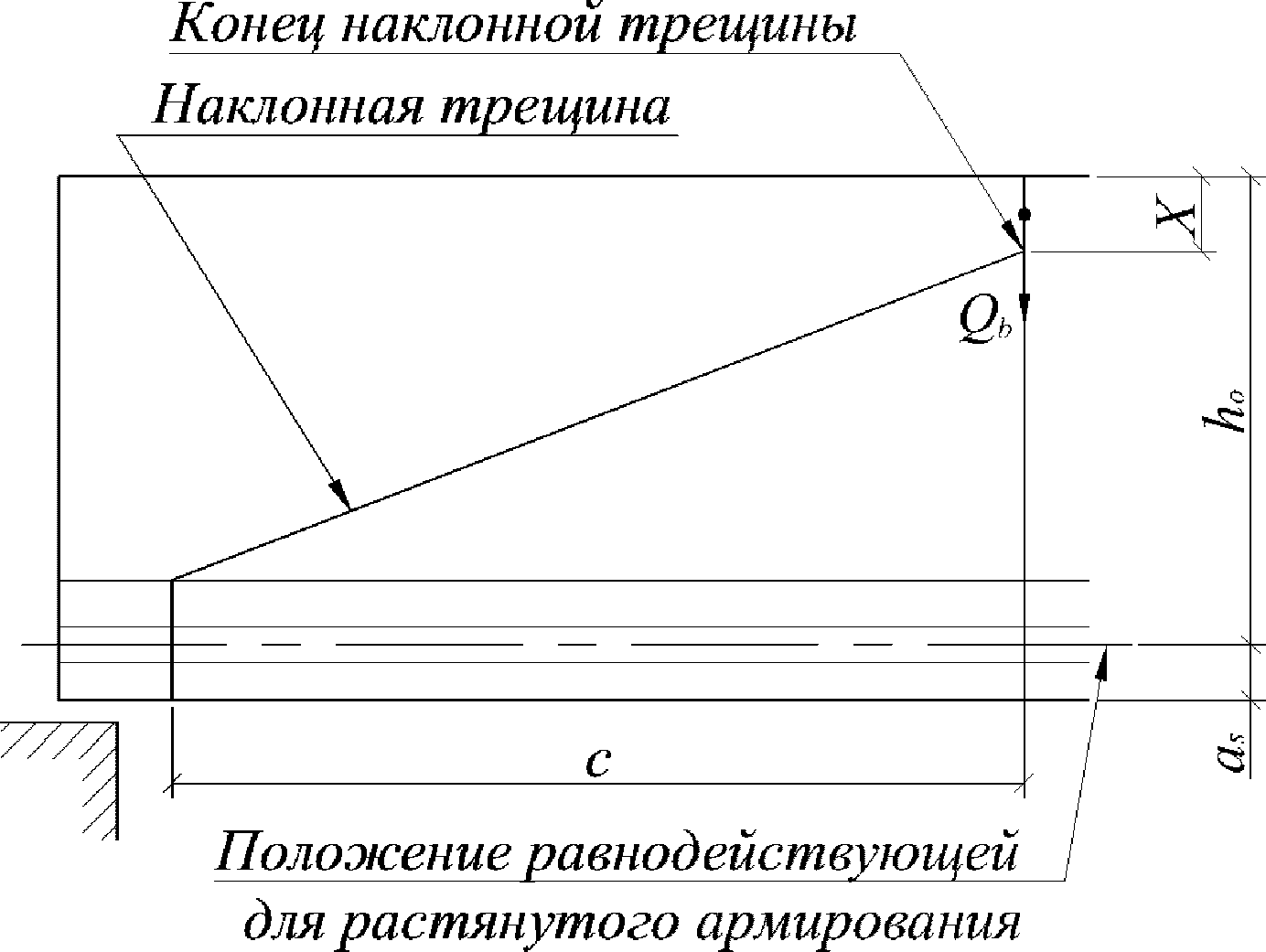
Для хомутов, расположенных перпендикулярно к продольной оси элемента, коэффициент, учитывающий расположение хомутов
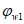 ,
определяется по формуле:
,
определяется по формуле:
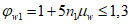 (5.3)
(5.3)
иначе
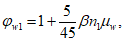 (5.4)
(5.4)
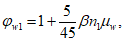 (5.4)
(5.4)
В
формулах (5.2)
-
(5.5)
:
n
1
- коэффициент приведения поперечного армирования к бетону;
E
sw
- модуль упругости поперечной арматуры, кН/м
2
;
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
.
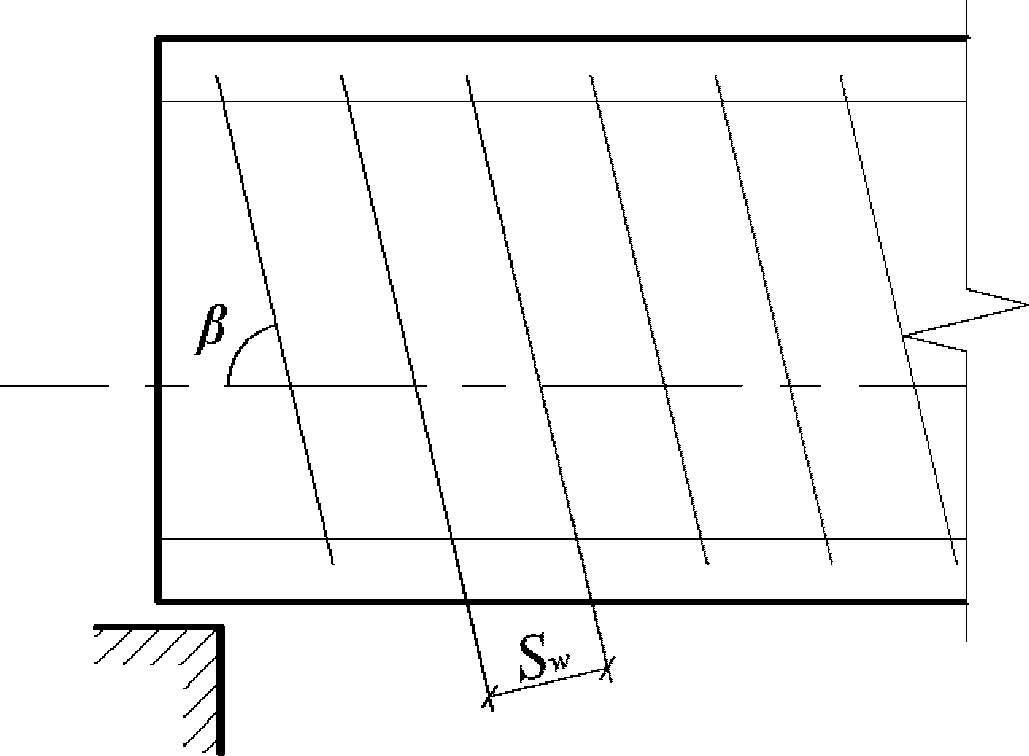
к продольной оси элемента
Доля поперечного армирования
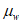 определяется по формуле:
определяется по формуле:
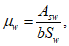 (5.6)
(5.6)
где
A
sw
-
площадь сечения ветвей хомутов, расположенных в одной плоскости
(рисунок 5.5)
, м
2
;
S
w
- кратчайшее расстояние между хомутами
(рисунок 5.5)
, м.
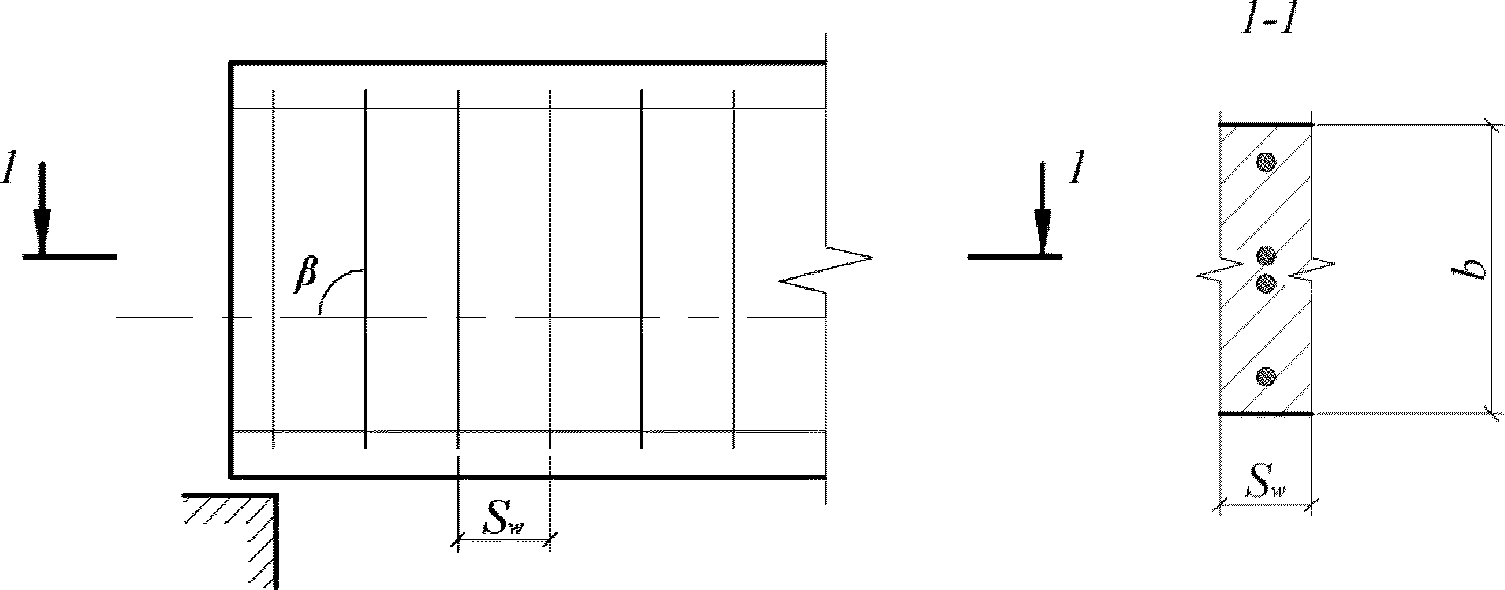
Коэффициент, зависящий от прочности бетона
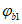 ,
определяется по формуле:
,
определяется по формуле:
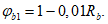 (5.7)
(5.7)
Расчетное сопротивление бетона сжатию
R
b
подставляется в формулу в МПа.
Рабочая высота сечения, пересекающего конец наклонной трещины
h
0
, определяется по формуле:
h
0
=
H
-
a
s
, (5.8)
где
H
- высота сечения в конце наклонной трещины, м;
a
s
-
расстояние между нижней гранью сечения и равнодействующей усилий в растянутой арматуре в конце наклонной трещины согласно
3.1.1
для изгибаемых элементов и согласно
4.1.3.2
для внецентренно сжатых элементов, м.
Предварительно рекомендуется определить наибольшие скалывающие (касательные) напряжения
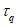 от нормативной нагрузки согласно
5.2.1
, так как при
от нормативной нагрузки согласно
5.2.1
, так как при
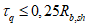 , расчет наклонного сечения на действие поперечной силы допускается не производить.
, расчет наклонного сечения на действие поперечной силы допускается не производить.
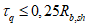 , расчет наклонного сечения на действие поперечной силы допускается не производить.
, расчет наклонного сечения на действие поперечной силы допускается не производить.
R
b,sh
-
расчетное сопротивление бетона скалыванию при изгибе согласно
таблице 7.6
СП 35.13330, кН/м
2
.
Расчет наклонных сечений элементов на действие поперечной силы следует производить из условия:
Q
I
<=
Q
ult
, (5.9)
где
Q
I
- поперечная сила от расчетных нагрузок в конце наклонного сечения.
В запас прочности допускается принимать максимальное значение поперечной силы
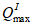 , на исследуемом участке, кН;
, на исследуемом участке, кН;
Q
ult
- предельная поперечная сила, кН.
Предельную поперечную силу
Q
ult
рекомендуется определять по формуле:
Q
ult
=
Q
si
+
Q
sw
+
Q
b
, (5.10)
где
Q
si
- предельные усилия в отогнутой арматуре, кН;
Q
sw
-
предельные усилия в хомутах, кН;
Q
b
-
предельное усилие в бетоне сжатой зоны, кН.
Предельное усилие в отогнутой арматуре
Q
si
определяется по формуле:
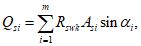 (5.11)
(5.11)
где
i
- номер отогнутого ряда армирования, пересекающего наклонную трещину;
m
- количество отогнутых рядов армирования, пересекающих наклонную трещину;
R
swk
-
расчетное сопротивление отогнутых рядов армирования с учетом коэффициента условий работы
m
a
4
(рисунок 5.6)
, кН/м
2
;
A
si
-
площадь
i
-го отогнутого ряда армирования, пересекающего наклонную трещину
(рисунок 5.6)
, м
2
;
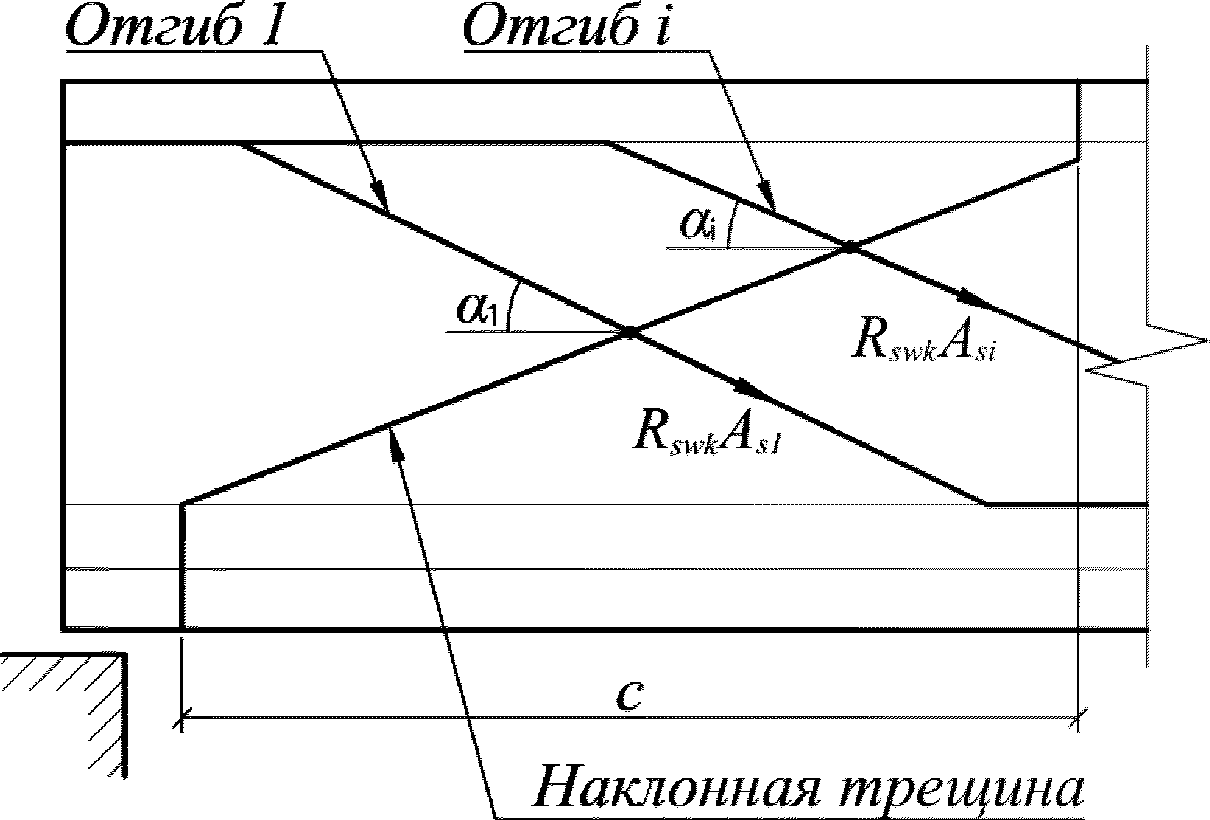
Предельные усилия в хомутах
Q
sw
определяются по формуле:
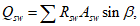 (5.12)
(5.12)
где
R
sw
- расчетное сопротивление поперечного армирования с учетом коэффициента условий работы
m
a
4
(рисунок 5.7)
, кН/м
2
;
A
sw
- площадь сечения ветвей хомутов, пересекающих наклонную трещину или наклонных стержней имеющих достаточную длину заделки в бетон
(рисунок 5.7)
, м
2
;
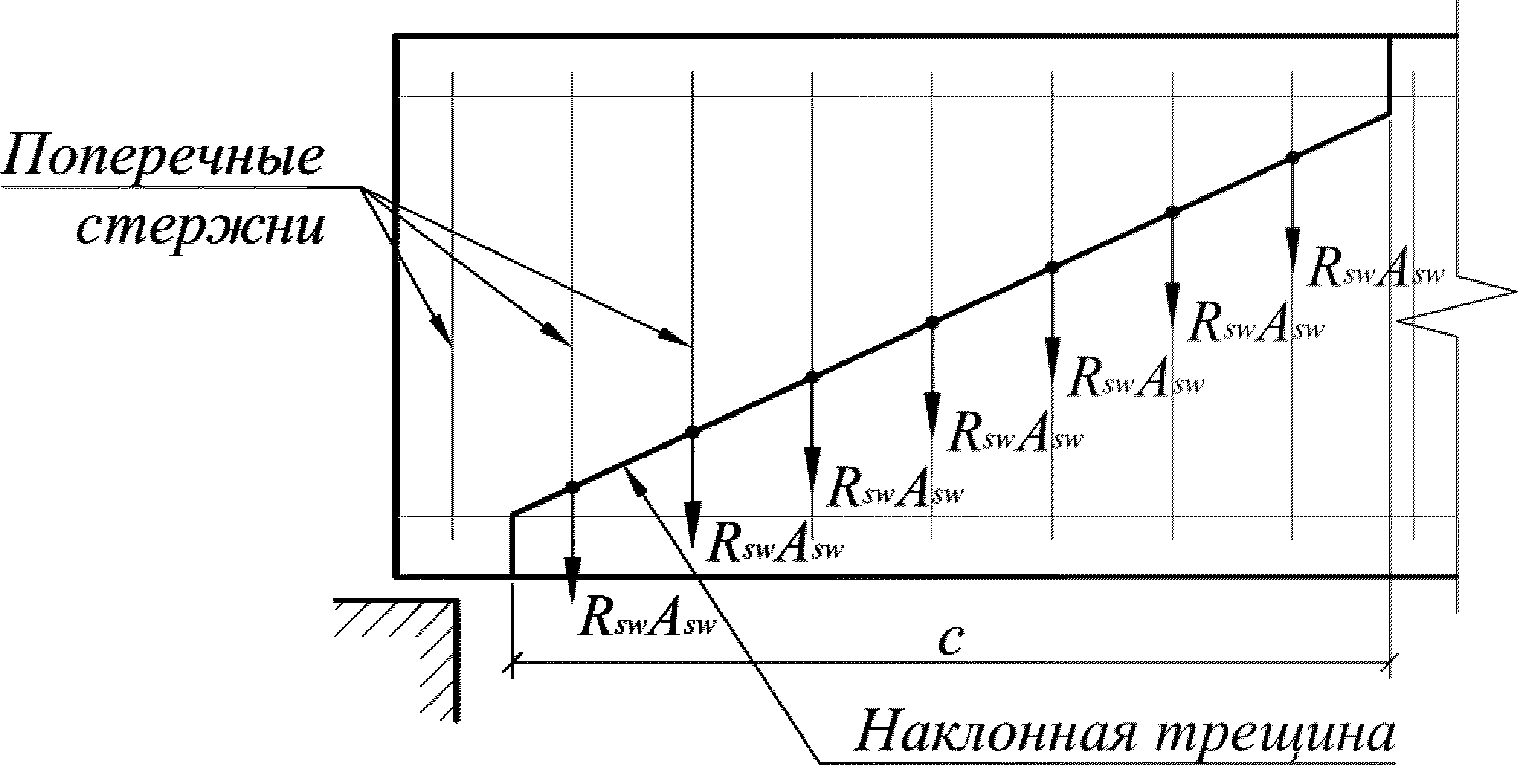
Расчетное сопротивление отогнутых рядов армирования
R
swk
и расчетное сопротивление поперечного армирования
R
sw
с учетом коэффициента условий работы
m
a
4
определяются по формулам:
В
формулах (5.13)
-
(5.14)
:
n
1
- коэффициент приведения поперечного армирования к бетону;
R
sk
-
расчетное сопротивление стали отогнутых рядов армирования, кН/м
2
;
R
s
- расчетное сопротивление стали поперечных стержней, кН/м
2
.
Если в сварных каркасах диаметр хомутов из арматурной стали класса А400 менее 1/3 максимального диаметра продольных стержней, то:
R
sw
<= 245 МПа - при диаметре хомутов 6 или 8 мм;
R
sw
<= 255 МПа - при диаметре хомутов 10 мм и более.
Предельное усилие в бетоне сжатой зоны
Q
b
определяется по формуле:
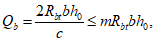 (5.15)
(5.15)
где
R
bt
- расчетное сопротивление бетона растяжению согласно
таблице 7.6
СП 35.13330, кН/м
2
;
b
- толщина стенки (ребра) или ширина сплошной плиты, м;
h
0
- рабочая высота сечения, пересекающего конец наклонной трещины
(рисунок 5.8)
, м;
c
- длина проекции невыгоднейшего наклонного сечения на продольную ось элемента
(рисунок 5.8)
, м;
m
- коэффициент условий работы.
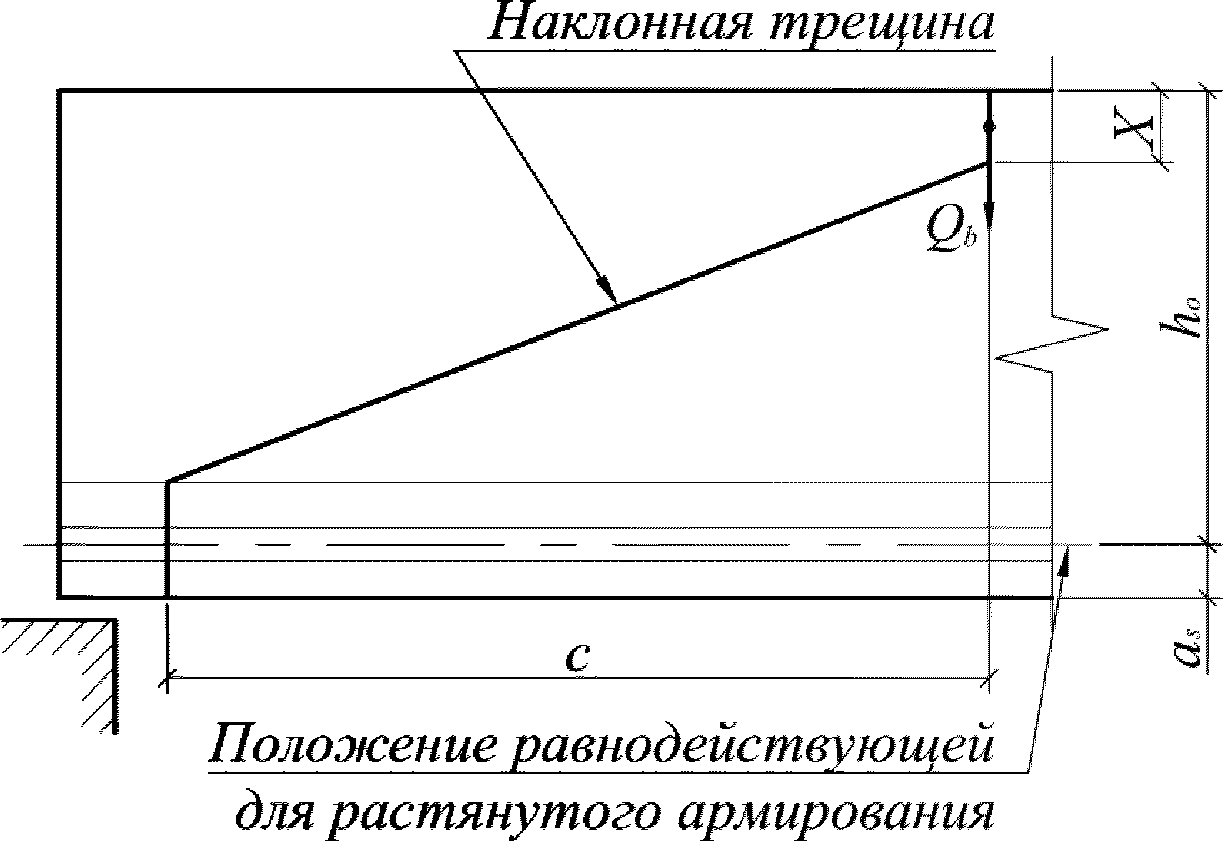
относительно наклонной трещины
Длина проекции невыгоднейшего наклонного сечения на продольную ось элемента
c
определяется сравнительными расчетами. Расчет рекомендуется производить с помощью компьютерных средств путем изменения положения наклонного сечения по длине элемента
(рисунок 5.9)
.
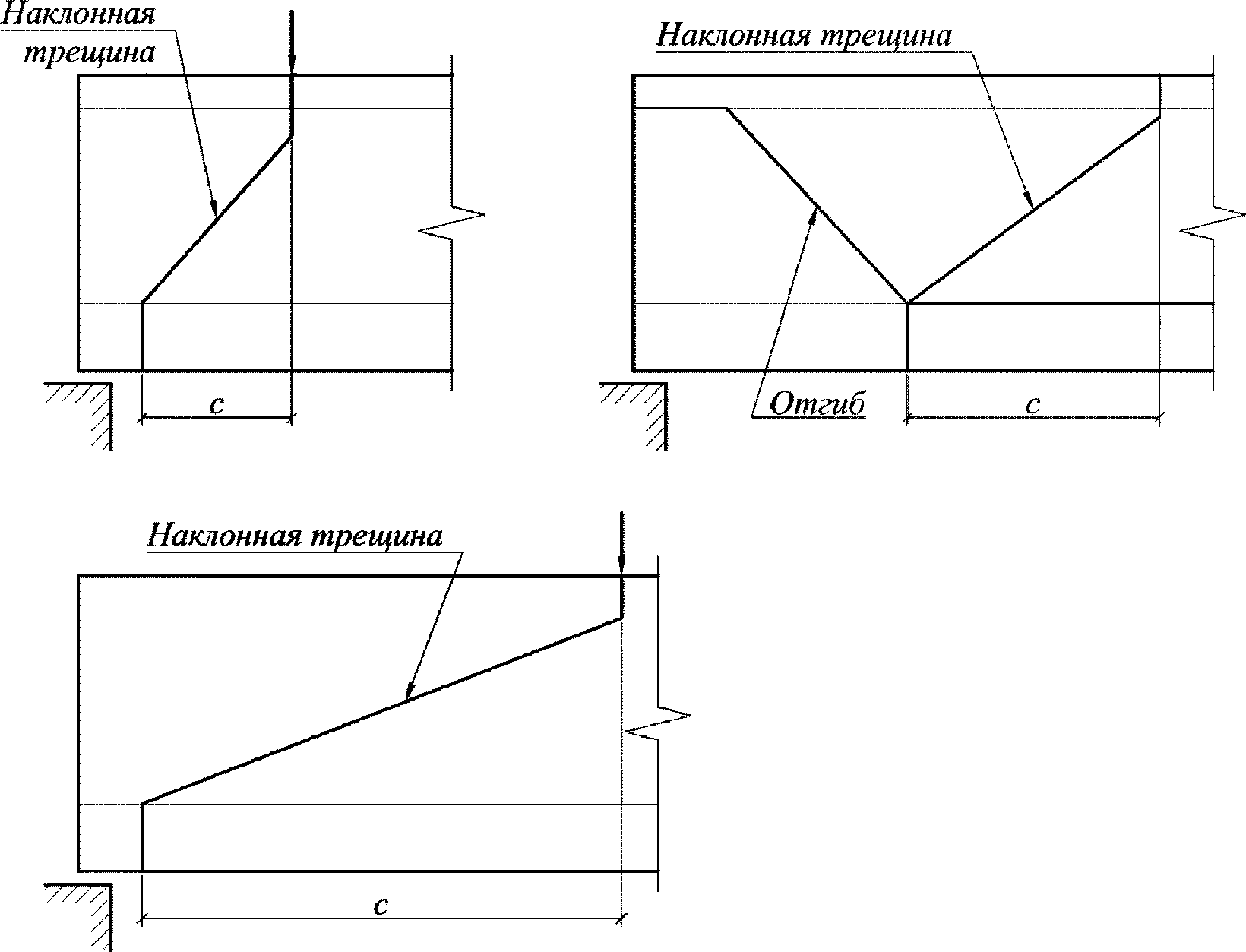
в ходе сравнительных расчетов
Коэффициент условий работы
m
определяется по формуле:
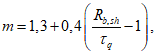 (5.16)
(5.16)
1,3 <=
m
<= 2,5
.
(5.17)
Рабочая высота сечения, пересекающего конец наклонной трещины
h
0
, определяется по формуле:
h
0
=
H
-
a
s
, (5.18)
где
H
- высота сечения в конце наклонной трещины, м;
a
s
-
расстояние между нижней гранью сечения и равнодействующей усилий в растянутой арматуре в конце наклонной трещины согласно
3.1.1
для изгибаемых элементов и согласно
4.1.3.2
для внецентренно сжатых элементов, м.
Предельный момент для наклонного сечения
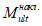 определяется по формуле:
определяется по формуле:
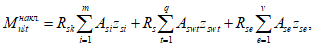 (5.19)
(5.19)
где
R
sk
-
расчетное сопротивление стали отогнутых рядов армирования, кН/м
2
;
i
- номер отогнутого ряда армирования;
m
- количество отогнутых рядов армирования;
A
si
-
площадь
i
-го отогнутого ряда армирования, пересекающего наклонную трещину, м
2
;
z
si
- кратчайшее расстояние между
i
-м отогнутым рядом армирования, пересекающим наклонную трещину, и равнодействующей усилий в сжатой зоне бетона
(рисунок 5.10)
, м;
R
s
- расчетное сопротивление стали поперечных стержней, кН/м
2
;
t
- номер группы поперечных стержней армирования;
q
- количество групп поперечных стержней армирования;
A
swt
-
площадь сечения ветвей
t
-ой группы поперечных стержней, пересекающей наклонную трещину и имеющих достаточную длину заделки в бетон
(рисунок 5.10)
, м
2
;
z
swt
- кратчайшее расстояние между
t
-ой группы поперечных стержней, пересекающей наклонную трещину, и равнодействующей усилий в сжатой зоне бетона
(рисунок 5.10)
, м;
R
se
-
расчетное сопротивление стали продольных стержней, кН/м
2
;
e
- номер продольного стержня, пересекающего наклонную трещину;
v
- количество продольных стержней, пересекающих наклонную трещину;
A
se
- площадь
e
-го продольного ряда армирования, пересекающего наклонную трещину
(рисунок 5.10)
, м
2
;
z
swe
- кратчайшее расстояние между
e
-м продольным рядом армирования, пересекающим наклонную трещину, и равнодействующей усилий в сжатой зоне бетона
(рисунок 5.10)
, м.
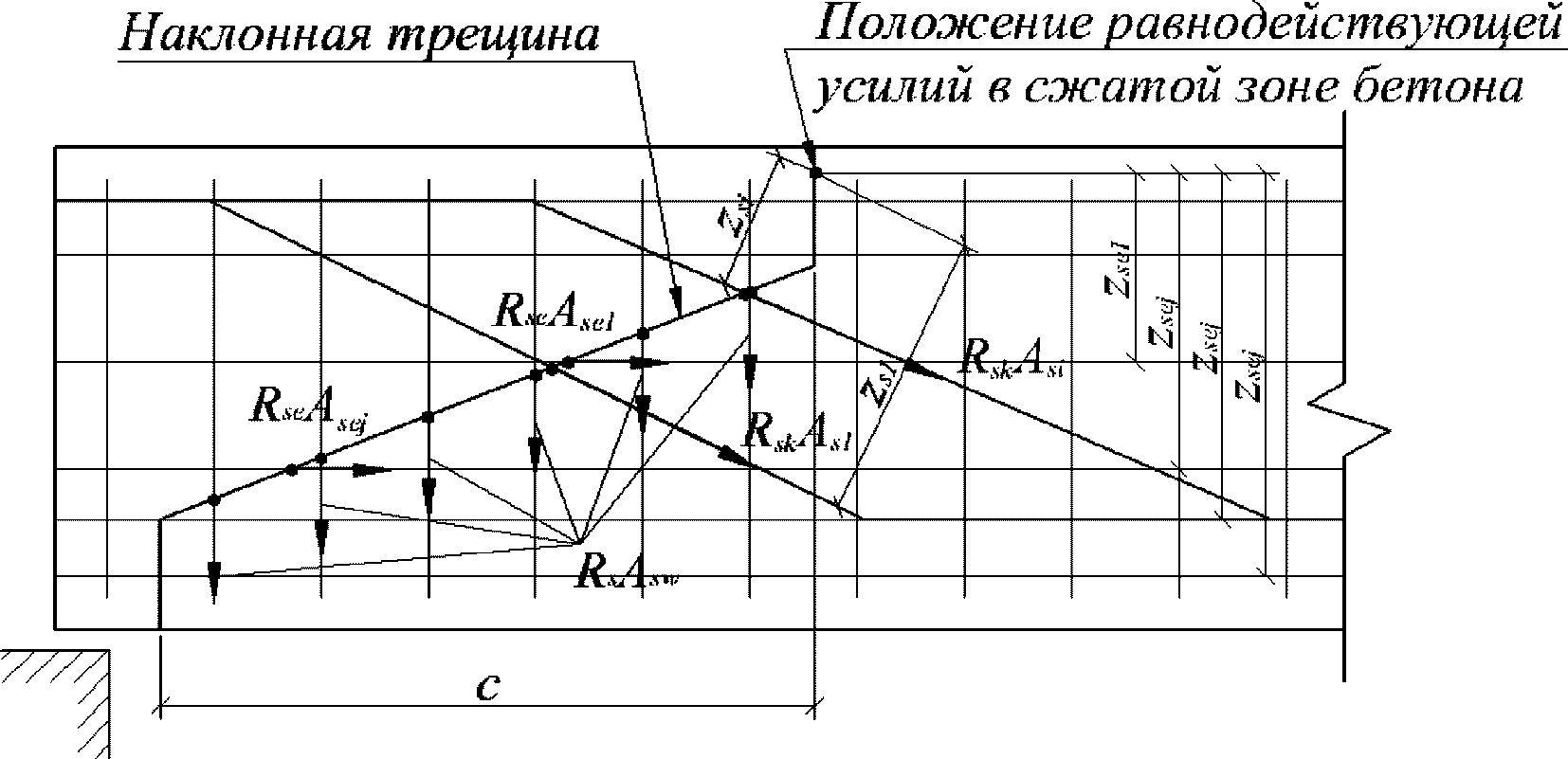
предельного усилия
Проверка прочности наклонного сечения на действие изгибающего момента заключается в выполнении условия:
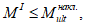 (5.20)
(5.20)
где
M
I
- момент от действия расчетных нагрузок в конце наклонной трещины. В запас прочности допускается принимать максимальное значение момента
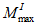 на исследуемом участке, кН·м.
на исследуемом участке, кН·м.
К расчетам по второй группе предельных состояний относятся расчеты по трещиностойкости и расчет ширины раскрытия наклонных трещин
(рисунок 5.11)
.
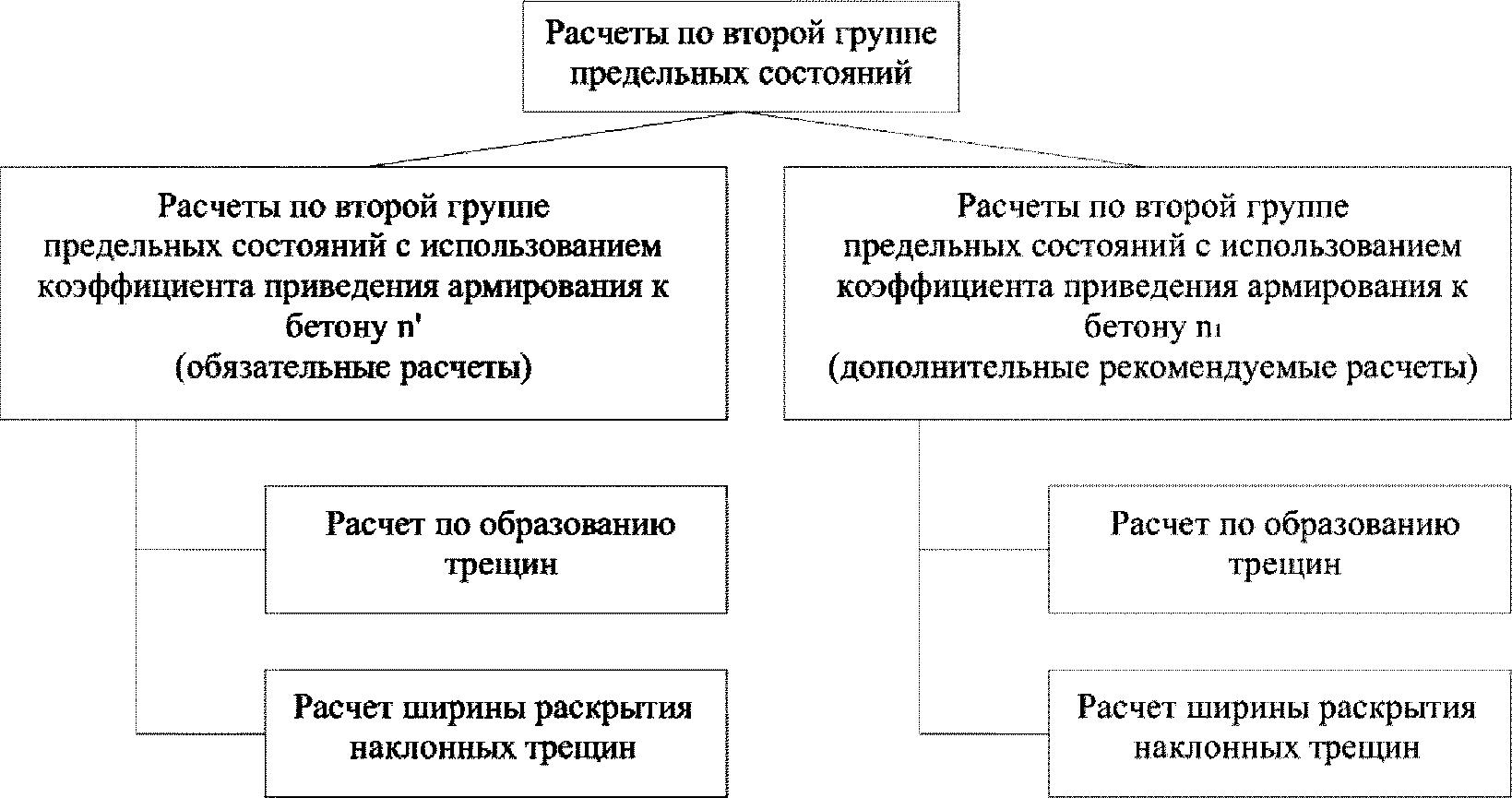
Согласно требованиям
п. 7.48
СП 35.13330 для расчетов на трещиностойкость (для расчета напряжений и геометрических характеристик) используется коэффициент приведения армирования к бетону, учитывающий влияние виброползучести бетона
n'.
Виброползучесть бетона - это длительный процесс, а усилия, на которые производится расчет по второй группе предельных состояний, возникают и на ранних стадиях эксплуатации конструкции. Поэтому авторы данного пособия также рекомендуют производить все проверки по второй группе предельных состояний с расчетом напряжений и геометрических характеристик сечения при коэффициенте приведения армирования к бетону
n
1
:
В
формулах (5.21)
-
(5.22)
:
E
s
- модуль упругости арматуры согласно
таблице 7.19
СП 35.13330, кН/м
2
;
E
b
- модуль упругости бетона согласно
таблице 7.11
СП 35.13330, кН/м
2
.
Расчет по образованию трещин заключается в ограничении наибольших скалывающих (касательных) напряжений
 :
:
 (5.23)
(5.23)
где
R
b,sh
-
расчетное сопротивление бетона скалыванию при изгибе согласно
таблице 7.6
СП 35.13330, кН/м
2
.
Наибольшие скалывающие (касательные) напряжения
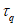 для элементов, подверженных воздействию поперечных сил, определяются по формуле:
для элементов, подверженных воздействию поперечных сил, определяются по формуле:
где
Q
II
- поперечная сила от действия нормативных нагрузок, кН;
S
от.
- статический момент инерции части, лежащей ниже или выше центра тяжести приведенного сечения, взятый относительно центра тяжести приведенного сечения, м
3
;
I
red
-
момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения согласно
3.1.2.1
или
4.2.1.2
, м
4
;
t
- ширина сечения в уровне центра тяжести приведенного сечения, м.
Если присутствует кручение, то дополнительные скалывающие (касательные) напряжения от кручения необходимо прибавить к
формуле (5.24)
.
Геометрические характеристики сечения вычисляются как для внецентренно сжатого элемента согласно
4.2.1.2
или изгибаемого элемента согласно
3.1.2.1
в зависимости от типа напряженно-деформированного состояния.
Для изгибаемых элементов:
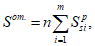 (5.25)
(5.25)
где
n
- коэффициент приведения армирования к бетону;
i
- номер ряда армирования;
m
- количество рядов армирования;
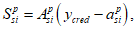 (5.26)
(5.26)
где
 - площадь
i
-го растянутого ряда армирования
(рисунок 5.12)
, м
2
;
- площадь
i
-го растянутого ряда армирования
(рисунок 5.12)
, м
2
;
y
cred
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения согласно
3.1.2.1
, м;
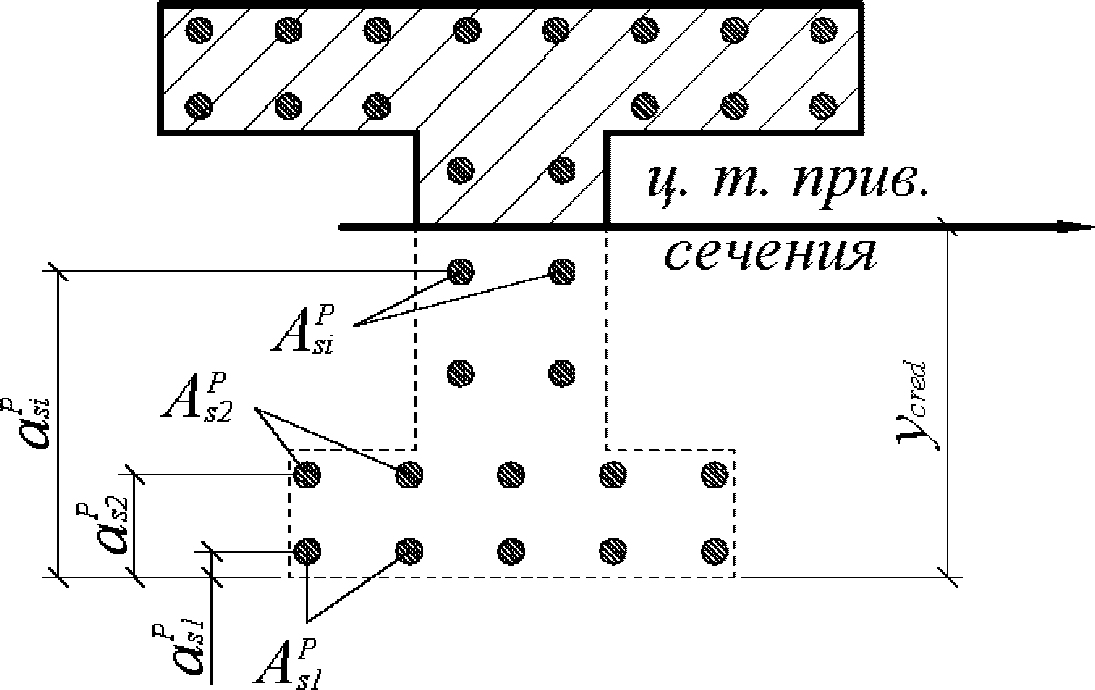
Для удобства расчетов вводятся следующие критерии определения состояния арматуры:
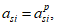 (5.28)
(5.28)
В
формулах (5.27)
-
(5.29)
:
a
- высота растянутой зоны бетона согласно
3.1.2.1
, м;
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м;
A
si
- площадь
i
-го ряда армирования, м
2
.
Для внецентренно сжатых элементов:
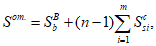 (5.30)
(5.30)
где
 - статический момент инерции, взятый относительно центра тяжести приведенного сечения, бетонной части сечения, лежащей выше центра тяжести приведенного сечения, м
3
;
- статический момент инерции, взятый относительно центра тяжести приведенного сечения, бетонной части сечения, лежащей выше центра тяжести приведенного сечения, м
3
;
Сложные сечения рекомендуется разбивать на отдельные участки правильной геометрической формы. Тогда статический момент инерции, взятый относительно центра тяжести приведенного сечения, бетонной части сечения, лежащей выше центра тяжести приведенного сечения
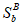 ,
определяется по формуле:
,
определяется по формуле:
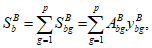 (5.31)
(5.31)
где
g
- номер участка сечения, лежащий выше центра тяжести приведенного сечения;
p
- количество участков сечения, лежащих выше центра тяжести приведенного сечения;
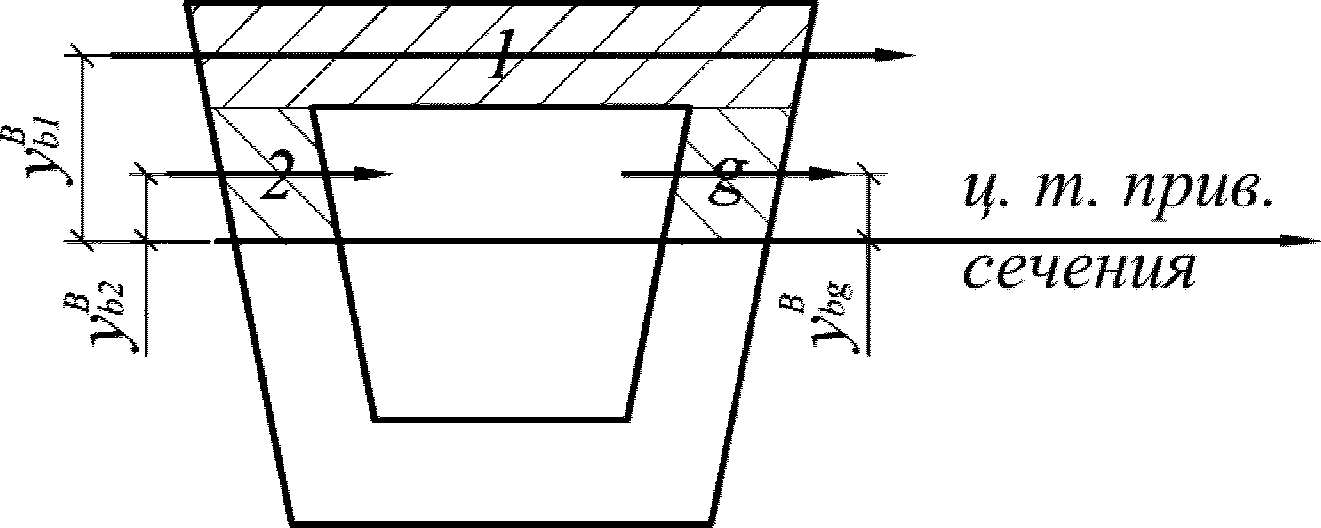
Статический момент инерции, взятый относительно центра тяжести приведенного сечения,
i
-го сжатого ряда армирования, лежащего выше центра тяжести приведенного сечения
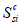 ,
определяется по формуле:
,
определяется по формуле:
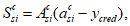 (5.32)
(5.32)
где
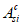 - площадь
i
-го сжатого ряда армирования, лежащего выше центра тяжести приведенного сечения
(рисунок 5.14)
, м
2
;
- площадь
i
-го сжатого ряда армирования, лежащего выше центра тяжести приведенного сечения
(рисунок 5.14)
, м
2
;
y
cred
- расстояние между нижней гранью сечения и центром тяжести приведенного сечения согласно
4.2.1.2
, м.
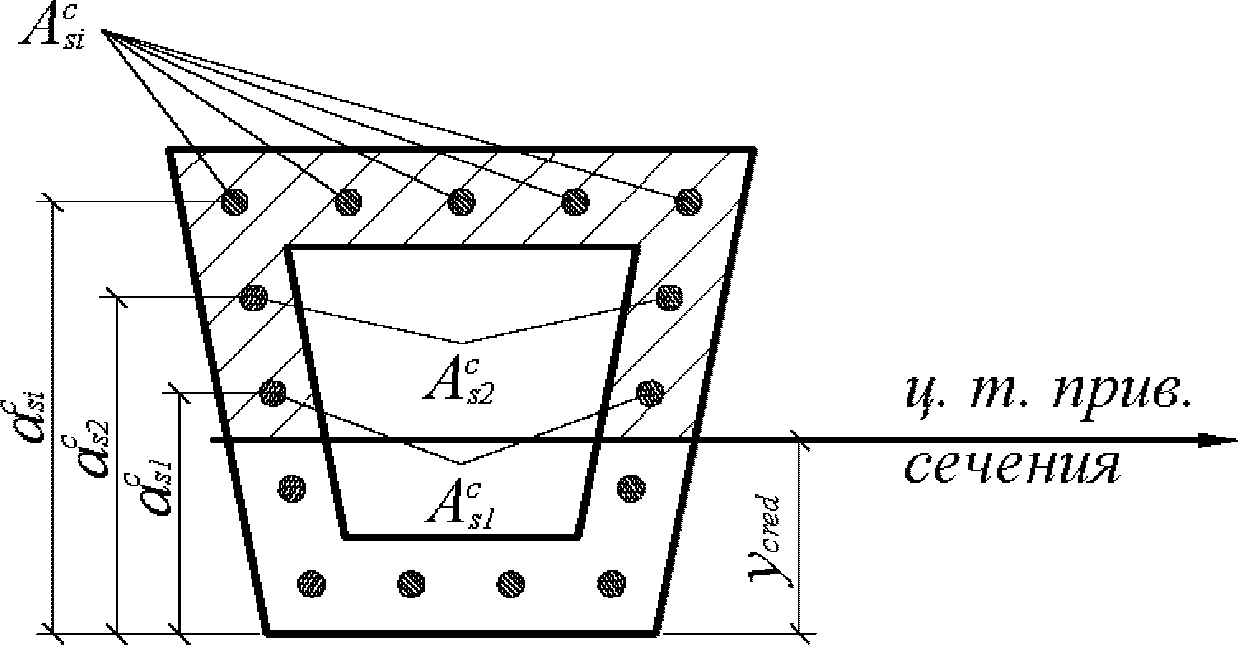
Для удобства расчетов вводятся следующие критерии определения состояния арматуры:
при
a
si
> a
, (5.33)
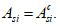 (5.35)
(5.35)
В
формулах (5.34)
-
(5.36)
:
a
- высота растянутой зоны бетона согласно
4.2.1.2
, м.
Расчет заключается в определении ширины раскрытия наклонных трещин
a
cr
и сравнении ее с предельным значением расчетной ширины раскрытия трещин
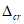 .
.
Расчетная ширина раскрытия нормальных трещин
a
cr
определяется по формуле:
где
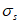 -
напряжения в поперечной и продольной арматуре стенок (ребер), кН/м
2
;
-
напряжения в поперечной и продольной арматуре стенок (ребер), кН/м
2
;
E
s
- модуль упругости смешанного армирования, пересекающего наклонную трещину, кН/м
2
;
Ограничение ширины раскрытия нормальных трещин производится согласно условию:
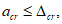 (5.37)
(5.37)
где
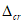 - предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
- предельное значение расчетной ширины раскрытия трещин, принимаемое по
таблице 7.24
СП 35.13330, см.
Напряжения в поперечной и продольной арматуре стенок (ребер)
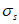 определяются по формуле:
определяются по формуле:
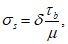 (5.38)
(5.38)
где
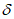 - коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных трещин;
- коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных трещин;
Коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных трещин
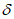 определяется по формуле:
определяется по формуле:
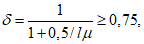 (5.39)
(5.39)
где
l
- длина предполагаемой наклонной трещины, см.
Длина предполагаемой наклонной трещины
l
в двутавровых балках измеряется между вутами поясов, а в тавровых - от ближайшего к нейтральной оси растянутого ряда армирования рабочей продольной арматуры до начала вута верхнего пояса
(рисунок 5.15)
.
Допускается определять ширину раскрытия наклонных трещин при наклоне трещины к продольной оси элемента под углом 45°.
Коэффициент армирования стенки стержнями, пересекающими наклонную трещину
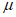 ,
определяется по формуле:
,
определяется по формуле:
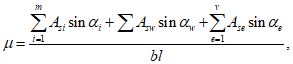 (5.40)
(5.40)
где
i
- номер отогнутого ряда армирования, пересекающего наклонную трещину;
m
- количество отогнутых рядов армирования, пересекающих наклонную трещину;
A
si
-
площадь
i
-го отогнутого ряда армирования, пересекающего наклонную трещину, м
2
;
A
sw
- площадь сечения ветвей хомутов, пересекающих наклонную трещину или наклонных стержней имеющих достаточную длину заделки в бетон (рисунок 63), м
2
;
e
- номер продольного стержня, пересекающего наклонную трещину;
v
- количество продольных стержней, пересекающих наклонную трещину;
A
se
- площадь
e
-го продольного стержня, пересекающего наклонную трещину, м
2
;
b
- толщина стенки (ребра) или ширина сплошной плиты, м.
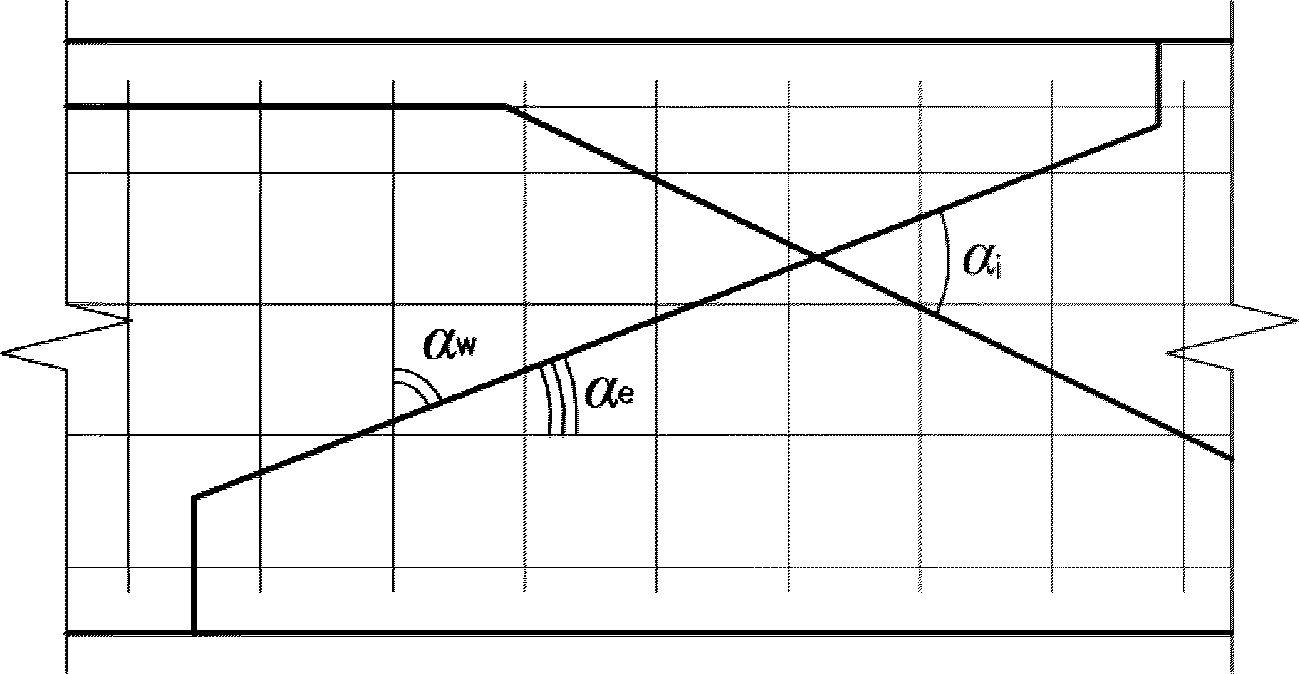
армирования к наклонной трещине
Модуль упругости смешанного армирования, пересекающего наклонную трещину
E
s
,
определяется по формуле:
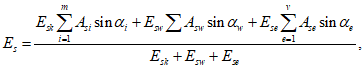 (5.41)
(5.41)
где
E
sk
-
модуль упругости отогнутых рядов армирования, пересекающих наклонную трещину, кН/м
2
;
E
sw
- модуль упругости хомутов, пересекающих наклонную трещину, кН/м
2
;
E
se
- модуль упругости продольных стержней, пересекающих наклонную трещину, кН/м
2
.
Обобщенный коэффициент раскрытия трещин
 определяется по формуле:
определяется по формуле:
 (5.42)
(5.42)
где
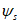 -
коэффициент раскрытия трещин для отогнутых стержней, см;
-
коэффициент раскрытия трещин для отогнутых стержней, см;
Для гладкой стержневой арматуры, арматурных пучков из гладкой проволоки и для стальных закрытых канатов коэффициенты раскрытия трещин
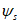 ,
,
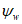 и
и
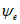 определяются по формулам:
определяются по формулам:
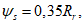 (5.43)
(5.43)
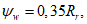 (5.44)
(5.44)
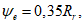 (5.45)
(5.45)
где
R
r
-
радиус армирования, см.
Для стержневой арматуры периодического профиля, проволок периодического профиля класса Вр, пучков из этой проволоки, канатов класса К7 и пучков из них, стальных канатов со спиральной и двойной свивкой, а также для любой арматуры в стенках коэффициенты раскрытия трещин
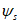 ,
,
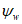 и
и
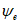 определяются по формулам:
определяются по формулам:
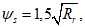 (5.46)
(5.46)
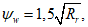 (5.47)
(5.47)
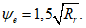 (5.48)
(5.48)
Радиус армирования
R
r
определяется по формуле:
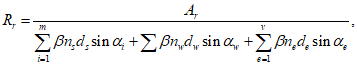 (5.49)
(5.49)
где
A
r
- площадь зоны взаимодействия для наклонного сечения, см
2
;
n
s
-
число арматурных элементов с одинаковым номинальным диаметром
d
s
;
d
s
-
диаметр отогнутых стержней, см;
n
w
- число арматурных элементов с одинаковым номинальным диаметром
d
w
;
d
w
- диаметр поперечных стержней, см;
n
e
-
число арматурных элементов с одинаковым номинальным диаметром
d
e
;
d
e
-
диаметр продольных стержней, см.
Для тонкостенных элементов допускается принимать площадь зоны взаимодействия
A
r
=
lb,
исходя из предположения, что радиус взаимодействия армирования с бетоном полностью охватывает толщину стенки.
Для непрямоугольных сечений с арматурой, равномерно распределенной по контуру, радиус взаимодействия принимается
r
=
3d.
Для пучков и канатов диаметр
d
соответствует наружному контуру арматурного элемента, а
r
= 5
d.
Во всех остальных случаях
r
= 6
d.
Сумма
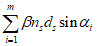 определяется по формуле:
определяется по формуле:
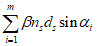 определяется по формуле:
определяется по формуле:
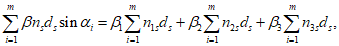 (5.50)
(5.50)
где
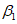 -
коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
-
коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
n
1
s
-
количество одиночных стержней в
i
-ом отогнутом ряду армирования;
n
2
s
-
количество сдвоенных стержней в
i
-ом отогнутом ряду армирования;
n
3
s
- количество строенных стержней в
i
-ом отогнутом ряду армирования.
Сумма
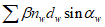 определяется по формуле:
определяется по формуле:
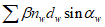 определяется по формуле:
определяется по формуле:
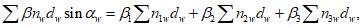 (5.51)
(5.51)
где
n
1
w
- количество одиночных стержней в составе группы поперечных стержней;
n
2
w
- количество сдвоенных стержней в составе группы поперечных стержней;
n
3
w
- количество строенных стержней в составе группы поперечных стержней.
Сумма
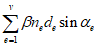 определяется по формуле:
определяется по формуле:
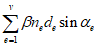 определяется по формуле:
определяется по формуле:
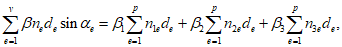 (5.52)
(5.52)
n
1
e
-
количество одиночных стержней в
i
-ом продольном ряду армирования;
n
2
e
-
количество сдвоенных стержней в
i
-ом продольном ряду армирования;
n
3
e
-
количество строенных стержней в
i
-ом продольном ряду армирования.
Методические рекомендации, пояснения и комментарии, относящиеся к требованиям по материалам, проектированию и конструированию, приведены в соответствии с нумерацией пунктов
СП 35.13330
.
7.2
Расчеты по образованию трещин, нормальных и наклонных к продольной оси элемента следует проводить для напрягаемой рабочей арматуры
(строка 2, столбец 2 таблицы)
.
7.10
Основной характеристикой уровня предварительного напряжения арматуры, задаваемой в проекте, является значение начального (т.н. контролируемого) усилия, поскольку установившееся усилие в арматуре, влияющее на напряженное состояние конструкции на стадии эксплуатации и монтажа равно контролируемому за вычетом потерь, произошедших к рассматриваемому моменту времени. Часть потерь в напрягаемой арматуре косвенно поддаются некоторой корректировке при проектировании (снижение трения о каналы при изменении трассирования и длины армоэлементов), но в целом являются функцией принятой системы напрягаемого армирования и реологических свойств бетона.
Контролируемое усилие назначается при проектировании. Сверху соответствующие напряжения в арматуре ограничены величиной расчетного сопротивления. Однако, учитывая некоторую условность назначения расчетного сопротивления через коэффициенты условий работы по назначению и коэффициенты надежности по материалу (см.
7.37
), было допущено увеличение расчетного сопротивления напрягаемой арматуры и, соответственно - контролируемого усилия (перетяжка) на стадии создания в конструкции предварительного напряжения (см.
7.45
) на 10% для стержневой арматуры и проволоки и на 5% - для канатов К7.
Аналогичный подход принят в европейских нормах (например Еврокод-2 EN 1992-2
[12]
) и европейских технических свидетельствах ЕТА, являющихся фактически стандартами СТО специализированных фирм по преднапряжению. В качестве контролируемого усилия предлагается принимать усилия, соответствующие 0,9 условного предела текучести, а максимальное усилие перетяжки - 0,95 условного предела текучести. К этим же значениям можно прийти и в
СП 35
, если в
п. 7.37
коэффициенты надежности по материалу (которые отражают опасения в стабильности качества отечественной напрягаемой арматуры) принять равным 1,0.
С учетом приведенных выше данных можно рекомендовать при использовании канатной арматуры по EN 10138-3 от проверенных производителей назначать напряжения контролируемого усилия не выше расчетных сопротивлений по
таблице 7.16
, но без учета коэффициентов по
таблице 7.15
. При этом на стадии эксплуатации (с учетом полных потерь) напряжения в любом сечении армоэлемента не должны превышать расчетного сопротивления.
Для контроля уровня натяжения напрягаемой арматуры в проектной документации требуется задавать помимо контролируемого усилия натяжения значение упругих удлинений (вытяжки) арматуры.
Удлинение арматуры при натяжении в общем случае следует определять по
п. 7.10
СП 35. Физический смысл этого выражения - суммирование (интегрирование) по длине пучка или его участка до сечения
x
удлинений условных отрезков пучка от изменяющегося по длине из-за наличия трения о стенки канала и на перегибах усилия натяжения. Входящие в выражение коэффициенты
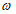 и
и
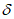 (принимаются по
таблице Р.2
приложения Р СП 35) суть коэффициенты трения, вызванного соответственно не учитываемыми при трассировании пучка местными отклонениями от прямолинейности и изгибами при поворотах трассы пучка. При этом
(принимаются по
таблице Р.2
приложения Р СП 35) суть коэффициенты трения, вызванного соответственно не учитываемыми при трассировании пучка местными отклонениями от прямолинейности и изгибами при поворотах трассы пучка. При этом
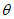 есть сумма углов поворота в горизонтальной и вертикальной плоскостях (в радианах) на участке
x.
есть сумма углов поворота в горизонтальной и вертикальной плоскостях (в радианах) на участке
x.
В этом пункте указывается, что значения удлинений
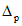 предварительно напряженной арматуры в общем случае определяются по
формуле (7.1)
:
предварительно напряженной арматуры в общем случае определяются по
формуле (7.1)
:
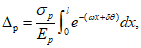
где
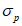 - напряжения, отвечающие контролируемому усилию и назначаемые с учетом требований
п. 7.14
;
- напряжения, отвечающие контролируемому усилию и назначаемые с учетом требований
п. 7.14
;
E
p
-
модуль упругости напрягаемой арматуры;
L -
расчетная длина арматурного элемента (расстояние от натяжного анкера до точки арматурного элемента с нулевым перемещением);
По этой формуле можно сделать два замечания.
Во-первых, угол поворота
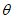 представляет собой дискретную функцию, постоянную на каждом участке между соседними перегибами напрягаемой арматуры. Поэтому целесообразно определять ее удлинение по участкам.
представляет собой дискретную функцию, постоянную на каждом участке между соседними перегибами напрягаемой арматуры. Поэтому целесообразно определять ее удлинение по участкам.
Во-вторых, приведенный в формуле интеграл является табличным и берется в замкнутом виде:
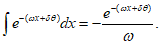
Поэтому на каждом
i
-м участке удлинение
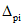 можно представить в виде:
можно представить в виде:
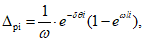
где
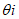 -
угол перелома арматуры в начале
i
-го участка;
-
угол перелома арматуры в начале
i
-го участка;
li -
длина
i
-го участка.
Тогда полное удлинение
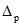 предварительно напряженной арматуры определится формулой:
предварительно напряженной арматуры определится формулой:
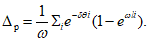
Формула
п. 7.10
СП 35 позволяет определить только величину упругого удлинения арматуры при натяжении. Однако при небольших длинах напрягаемой арматуры (для пучков из канатов К7 - менее 50 м) рекомендуется учитывать при определении проектной вытяжки арматуры другие сопутствующие факторы:
- упругую деформацию бетона от усилия натяжения пучков, натягиваемых одновременно:
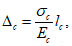
где
 - напряжение в бетоне на уровне центра тяжести сечения от усилия всех напрягаемых одновременно арматурных элементов;
- напряжение в бетоне на уровне центра тяжести сечения от усилия всех напрягаемых одновременно арматурных элементов;
E
c
- модуль упругости бетона;
l
c
- расчетная длина бетонного элемента до точки с нулевым перемещением;
- суммарное обмятие и затягивание клиньев в анкере
 . Данные указываются в документации на анкеры и куплеры и составляют 1 - 6 мм;
. Данные указываются в документации на анкеры и куплеры и составляют 1 - 6 мм;
- упругое удлинение натягиваемой арматуры на длине домкрата
l
d
(между опорной плоскостью и технологическим захватом)
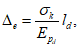
где
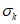 - напряжения в арматуре от контролируемого усилия натяжения арматуры без учета потерь.
- напряжения в арматуре от контролируемого усилия натяжения арматуры без учета потерь.
При большом объеме напрягаемых элементов и (или) их длине свыше 80 м и полигональном очертании рекомендуется корректировать проектные значения вытяжек арматуры путем:
- использования фактического значения модуля упругости арматуры, определенного по результатам ее испытаний;
- проведение контрольного натяжения армоэлемента с фиксацией усилия на глухом анкере с помощью специального силоизмерителя или натяжного домкрата, установленного в положении масляной подушки.
При определении фактического воздействия, создаваемого усилием натяжения напрягаемой арматуры, коэффициенты надежности по нагрузке следует принимать 1,1 или 0,9.
При контроле натяжения по усилиям на домкрате и одновременно контроле по вытяжке допускается принимать коэффициент надежности по нагрузке 1,0 (
п. 7.45
СП 35). В соответствии с
п. 7.86
СП 35 для составных по длине конструкций коэффициент надежности к усилиям в напрягаемой арматуре назначается менее 1,1 и более 0,9 в виде функции от количества пучков. Составные по длине конструкции характерны большим, чем монолитные количеством пучков и вероятность систематического отклонения контролируемых усилий в арматуре в них ниже.
7.11
Для напрягаемой арматуры, не имеющей концевых анкеров, место передачи сосредоточенных усилий на бетон следует принимать на расстоянии 2/3 длины зоны передачи напряжений, считая от конца зоны сцепления напрягаемого элемента с бетоном.
Длина зоны передачи усилий натяжения на бетон для канатов К7 регламентирована
таблицей 7.2 п. 7.11
СП 35. Для канатов классом прочности выше К7 1400 приведенных в
таблице 7.16
СП 35 длину зоны передачи рекомендуется увеличивать с коэффициентом, равным отношению значения класса к 1400.
7.12
В соответствии с требованиями
СП 35
передачу усилия на бетон от анкеров напрягаемой арматуры следует выполнять с использованием опорных закладных деталей и косвенного армирования, которые должны являться частью используемой конструктивно-технологической системы предварительного напряжения.
Косвенное армирование во всех системах преднапряжения выполняется в виде спирали из арматурной стали. Диаметры арматуры и спирали, количество витков спирали, класс арматурной стали (иногда не указан, но рекомендуется принимать не ниже А400) зависит от типа и размеров (мощности) анкера и приводится в документации фирмы-поставщика. Если поставка спиралей косвенного армирования не предусмотрена в комплектах анкеров ее следует проектировать из арматуры класса А400 (АIII) по
ГОСТ 5781
с геометрическими размерами по документации поставщика анкеров. Информация по спиралям косвенного армирования к анкерам ООО "СТС" (Россия) приведена на
рис. 6.1
-
6.4
.
Кроме спиралей косвенного армирования зону установки анкеров требуется дополнительно армировать стержневой арматурой в виде сеток.
Размеры анкеров, расстояние между анкерами и расстояние от оси анкера до края бетона даны для класса бетона Rbp = B20 (Rm = 25 МПа) перед натяжением.
Изменение диаметра каналообразователя возможно по согласованию с СТС.
Спираль косвенного армирования должна изготавливаться из стержневой арматуры класса не ниже А400 (III). Спираль косвенного армирования в комплект поставки не входит.
СТС оставляет за собой право на расширение ряда анкеров и изменение конструкции анкеров.
производства ООО "СТС"
<*> - Анкер АКП-4П имеет прямоугольную обойму и прямоугольную опорную плиту, поэтому размеры К1 и Л1 даны для короткой стороны анкера, а размеры К2 и Л2 даны для длинной стороны анкера.
Размеры анкеров, расстояние между анкерами и расстояние от оси анкера до края бетона даны для класса бетона Rbp = B20 (Rm = 25 МПа) перед натяжением.
Изменение диаметра каналообразователя возможно по согласованию с СТС.
Спираль косвенного армирования должна изготавливаться из стержневой арматуры класса не ниже А400 (III). Спираль косвенного армирования в комплект поставки не входит.
СТС оставляет за собой право на расширение ряда анкеров и изменение конструкции анкеров.
Рисунок 6.2 - Конструкция анкера клинового плитного
производства ООО "СТС"
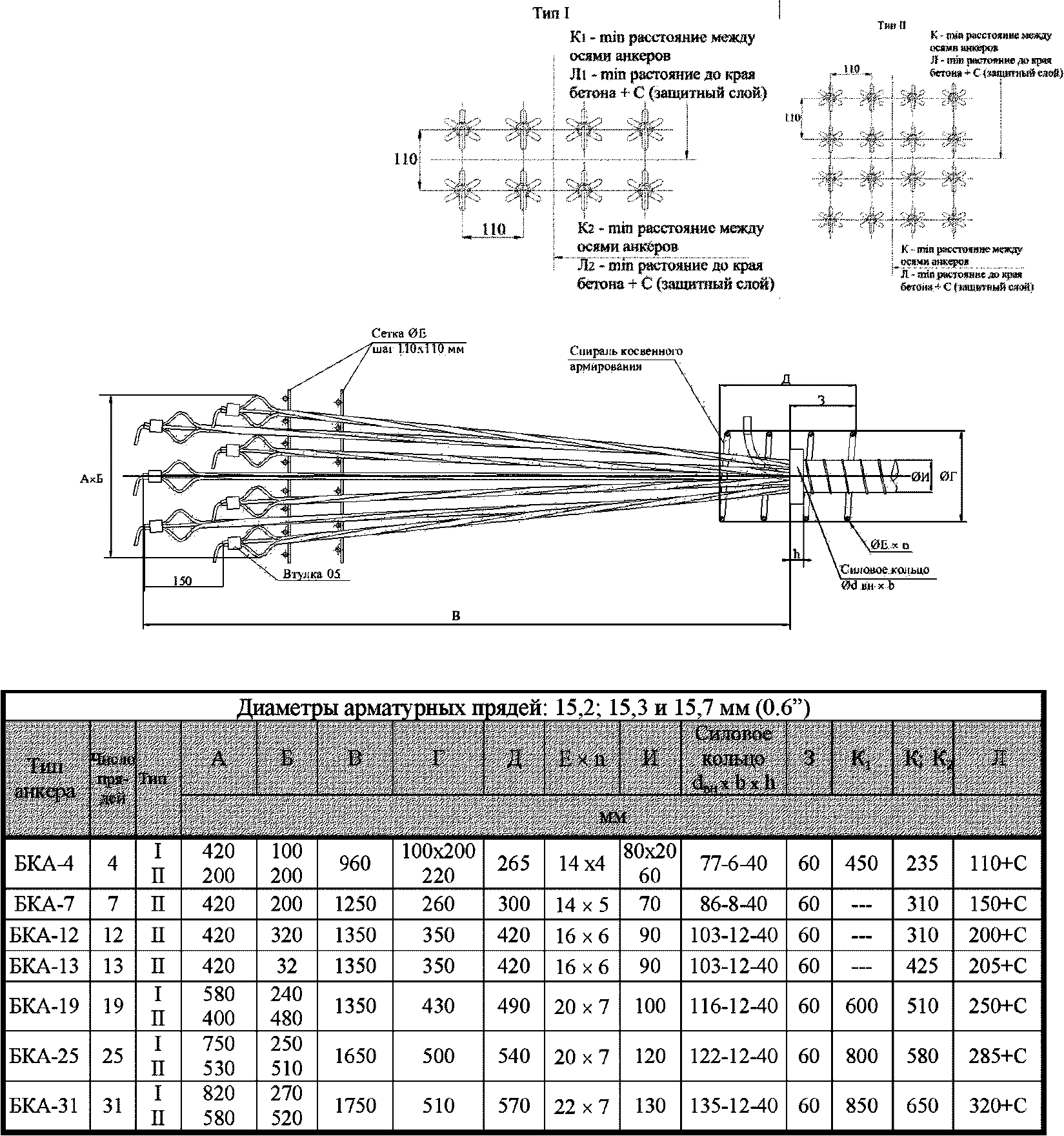
Расположение БКА, отличное от В, Тип I или Тип II, допускается по согласованию.
Размеры анкеров, расстояние между анкерами и расстояние от оси анкера до края бетона даны для класса бетона Rbp = B20 (Rm = 25 МПа) перед натяжением.
Изменение диаметра каналообразователя возможно по согласованию с СТС.
Спираль косвенного армирования должна изготавливаться из стержневой арматуры класса не ниже А400 (III). Спираль косвенного армирования в комплект поставки не входит.
СТС оставляет за собой право на расширение ряда анкеров и изменение конструкции анкеров.
Рисунок 6.3 - Конструкция бетонируемого каркасного анкера
производства ООО "СТС"
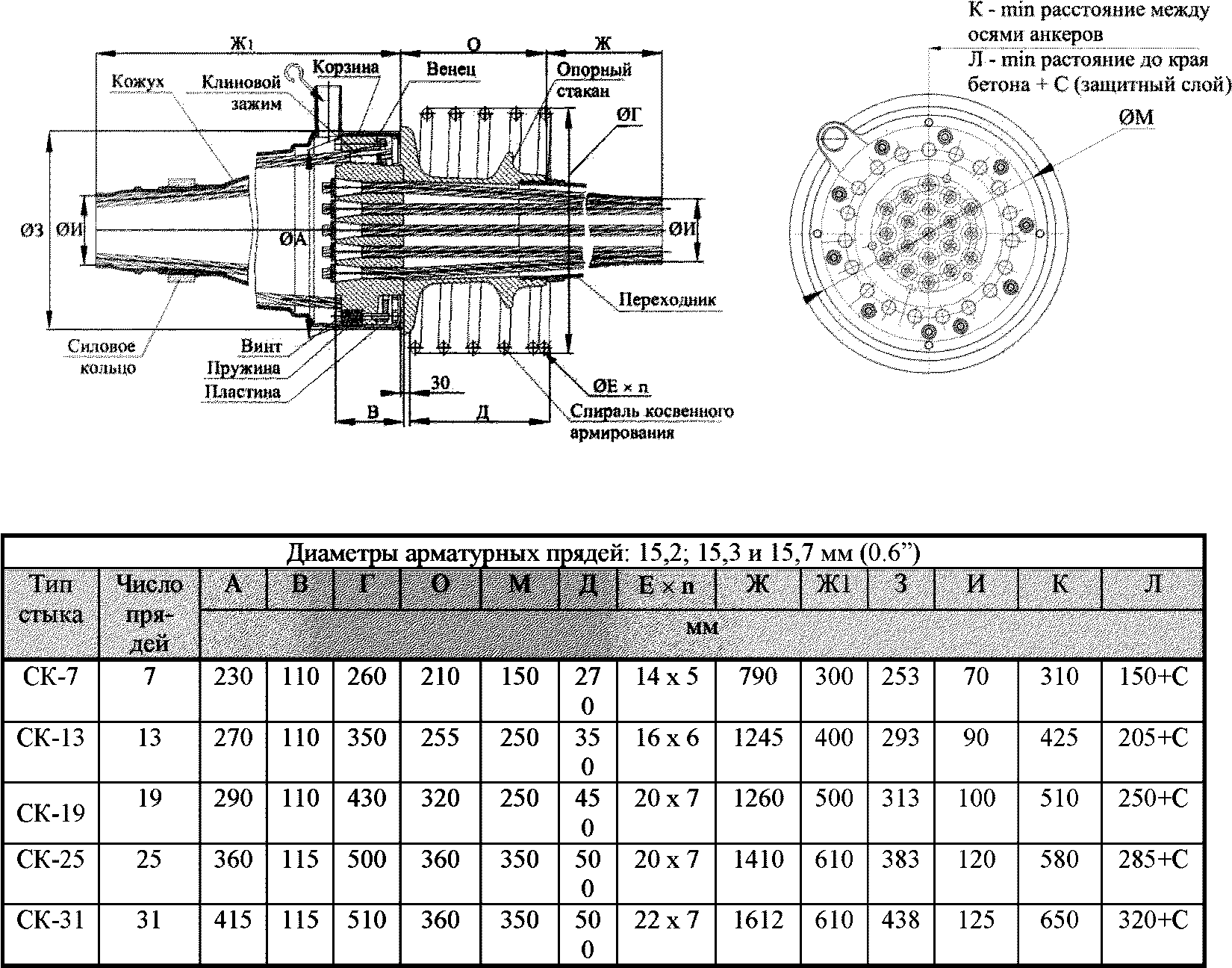
Размеры анкеров, расстояние между анкерами и расстояние от оси анкера до края бетона даны для класса бетона Rbp = B20 (Rm = 25 МПа) перед натяжением.
Изменение диаметра каналообразователя возможно по согласованию с СТС.
Спираль косвенного армирования должна изготавливаться из стержневой арматуры класса не ниже А400 (III). Спираль косвенного армирования в комплект поставки не входит.
СТС оставляет за собой право на расширение ряда анкеров и изменение конструкции анкеров.
клинового производства ООО "СТС"
Расчет сеток местного армирования следует производить методами теории упругости. Размеры сеток не должны создавать препятствий в установке в бетон анкеров, закладных деталей (анкерных стаканов), каналообразователей и спиралей косвенного армирования. Количество рядов сеток также подлежит определению расчетом. В случае применения системы СТС расчет и конструирование сеток местного армирования лежит на проектировщике. В системах преднапряжения европейских поставщиков (VSL, DSI, VT) данные о сетках местного армирования содержатся в документации поставщиков. Эти данные могут быть использованы при проектировании зон опирания аналогичных анкеров производства ООО "СТС".
При конструировании зон размещения концевых и стыковых анкеров следует учитывать рекомендации производителей по расположению анкеров между собой и относительно граней конструкции. Уменьшение этих размеров возможно только по согласованию фирм-производителей. Данные по сетке установке анкеров фирмы СТС приведены на
рис. 6.1
-
6.4
.
7.14
,
7.15
,
приложение Р
Напряжения в элементах системы преднапряжения конструкций подвержены изменению (главным образом - снижению) в процессе создания напряженного состояния и в последующие периоды. В основном в напрягаемой арматуре это происходит за счет т.н. потерь. Величина напряжений (усилий) в армоэлементах на различных стадиях существования - весьма важный показатель, поскольку определяет способность работы конструкции по принятым расчетным моделям и в том числе - без трещин.
Потери напряжений в арматуре разделяют на первые (возникающие в процессе обжатия бетона) и вторые (развивающиеся на стадии эксплуатации конструкции). В зависимости от принятой технологии создания преднапряжения в конструкции (натяжение арматуры до бетонирования на упоры или натяжения арматуры после бетонирования непосредственно на бетон конструкции) часть видов потерь в арматуре специфичны для одной или другой технологии.
Для конструкций, изготавливаемых по технологии создания преднапряжения с предварительным натяжением арматуры на упоры стенда или на форму, в которой бетонируется конструкция, характерны следующие причины первых потерь:
- деформации анкеров натяжных устройств;
- трение арматуры об огибающие приспособления стенда или формы при полигональном очертании напрягаемой арматуры;
- быстронатекающая релаксация (снижение напряжений в стали при постоянной деформации растяжения) напряжений в арматуре;
- быстронатекающая ползучесть бетона;
- температурный перепад между нагретой в результате термообработки бетона находящейся в нем арматуры и находящимися вне зоны нагрева неподвижными упорами, на которых закреплена эта арматура;
- упругая деформация стальной формы от усилия в напрягаемой арматуре (в этом случае, если форма является одновременно стендом).
Для случаев, в которых передача усилий преднапряжения производится сразу непосредственно на бетон готовой конструкции (натяжение после бетонирования или натяжение на бетон) существуют следующие причины возникновения первых потерь в напрягаемой арматуре:
- деформации концевых анкеров, устанавливаемых на бетон;
- трение арматуры о стенки закрытых и открытых каналов;
- первичная (быстронатекающая) релаксация напряжений в арматуре.
Ко вторым (эксплуатационным) потерям при натяжении на упоры следует относить:
- потери от длительных процессов усадки и ползучести бетона;
- длительная релаксация напряжений в напрягаемой арматуре.
В конструкциях с натяжением на бетон помимо упомянутых выше причин потерь напряжений в арматуре следует учитывать деформации стыков между блоками составных по длине конструкций (в первую очередь - пролетных строений). Что касается потерь за счет смятия бетона под витками спиральной или кольцевой напрягаемой таким образом арматуры - эта технология используется редко только при изготовлении свай-оболочек, и эти потери целесообразно перенести в нормативные документы по технологии этих работ.
Значения всех перечисленных потерь или методики их определения приведены в обязательном
приложении Р
к СП 35. Это приложение текстуально повторяет приложение 11* СНиП 2.05.03-84*
[13]
, в основном повторяет
приложение 11
СНиП 2.05.03-84
[14]
и базируется на
таблице 5
СНиП 2.03.01-84
[15]
. В связи с этим в
приложении Р
СП 35 накопились неточности, опечатки, морально устаревшие данные, а также положения, требующие комментариев. Ниже приведены комментарии и рекомендации к пользованию
приложением Р
.
Потери в напрягаемой арматуре, вызванные релаксацией напряжений в стали разделены в
таблице Р.1
в зависимости от вида арматуры (проволочная или стержневая) и способа создания преднапряжения (механический или электротермический для стержневой арматуры). При пользовании этим пунктом таблицы под термином "проволочная" следует понимать также арматурные канаты К7.
В формуле значения потерь в проволочной арматуре от релаксации допущена опечатка. Вместо Rph следует читать Rpn - нормативное сопротивление напрягаемой арматуры в соответствии с
п. 7.37
СП 35. Под
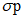 следует понимать полное суммарное напряжение в арматуре, для которой определяются потери от релаксации не только от преднапряжения без учета потерь (контролируемые напряжения), но и от внешних нагрузок (например, собственный вес), действующих на момент определения потерь.
следует понимать полное суммарное напряжение в арматуре, для которой определяются потери от релаксации не только от преднапряжения без учета потерь (контролируемые напряжения), но и от внешних нагрузок (например, собственный вес), действующих на момент определения потерь.
Проявление потерь от релаксации во времени следует учитывать в соответствии с
п. 7.14
СП 35, а именно в первых и вторых потерях учитывать релаксацию в равных долях (по 50%) от полных потерь по
приложению Р
.
Следует иметь в виду, что формулы определения потерь в проволочной арматуре от релаксации были получены в данном виде в 70-х годах прошлого века. В это время стабилизированной проволочной и канатной арматуры, отличающейся пониженной релаксацией, не существовало. Поэтому в данный пункт
таблицы Р.1
включено допущение (в виде примечания) по возможности уменьшать в два раза полученные потери при применении стабилизированной арматуры. Это относится к арматуре по
ГОСТ Р 53772
и EN 10138-3.
П.3 таблицы Р.1
, содержащий указания по определению потерь предварительного напряжения от деформаций анкеров, ориентирован на морально устаревшие конструкции анкеров, которые не применяют в настоящее время. Рекомендуется при определении
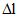 руководствоваться указаниями поставщиков анкеров. Для арматуры из канатов К7 в первом приближении рекомендуется принимать
руководствоваться указаниями поставщиков анкеров. Для арматуры из канатов К7 в первом приближении рекомендуется принимать
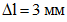 на анкер. Это соответствует средней величине затягивания конусов индивидуального закрепления канатов в анкерную обойму. Обжатие бетона под анкерами рекомендуется учитывать в размере 2 мм только при применении плоских не заделываемых в бетон прокладных листов под анкерными обоймами. При использовании закладных деталей (анкерных стаканов) обжатие бетона можно не учитывать.
на анкер. Это соответствует средней величине затягивания конусов индивидуального закрепления канатов в анкерную обойму. Обжатие бетона под анкерами рекомендуется учитывать в размере 2 мм только при применении плоских не заделываемых в бетон прокладных листов под анкерными обоймами. При использовании закладных деталей (анкерных стаканов) обжатие бетона можно не учитывать.
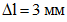 на анкер. Это соответствует средней величине затягивания конусов индивидуального закрепления канатов в анкерную обойму. Обжатие бетона под анкерами рекомендуется учитывать в размере 2 мм только при применении плоских не заделываемых в бетон прокладных листов под анкерными обоймами. При использовании закладных деталей (анкерных стаканов) обжатие бетона можно не учитывать.
на анкер. Это соответствует средней величине затягивания конусов индивидуального закрепления канатов в анкерную обойму. Обжатие бетона под анкерами рекомендуется учитывать в размере 2 мм только при применении плоских не заделываемых в бетон прокладных листов под анкерными обоймами. При использовании закладных деталей (анкерных стаканов) обжатие бетона можно не учитывать.
П.4 таблицы Р.1
содержит указания по определению потерь предварительного напряжения в арматуре от трения о стенки открытых и закрытых каналов при натяжении арматуры на бетон и об огибающие приспособления стенда - при натяжении на упоры до бетонирования. Фактически в обоих случаях потери определяют по одной формуле, в которой в случае натяжения на упоры полигональной арматуры коэффициент трения на прямолинейных участках
 .
.
При определении потери следует принимать во внимание следующее:
Коэффициенты
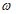 и
и
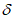 приведены в
табл. Р.2
в зависимости от видов поверхности каналов, в которых располагается напрягаемая арматура. При использовании комплектных систем преднапряжения, включая каналообразователи и арматуру коэффициенты
приведены в
табл. Р.2
в зависимости от видов поверхности каналов, в которых располагается напрягаемая арматура. При использовании комплектных систем преднапряжения, включая каналообразователи и арматуру коэффициенты
 и
и
 рекомендуется уточнять по рекомендациям поставщиков. Кроме того, могут предусматриваться технологические меры, позволяющие снизить значения этих коэффициентов. К таким мерам, например, можно отнести использование канатов К7 в состоянии поставки с покрытием водорастворимой защитной антикоррозионной смазкой. В этом случае коэффициенты
рекомендуется уточнять по рекомендациям поставщиков. Кроме того, могут предусматриваться технологические меры, позволяющие снизить значения этих коэффициентов. К таким мерам, например, можно отнести использование канатов К7 в состоянии поставки с покрытием водорастворимой защитной антикоррозионной смазкой. В этом случае коэффициенты
 и
и
 рекомендуется уточнить у поставщиков или опытным путем.
рекомендуется уточнить у поставщиков или опытным путем.
Потери предварительного напряжения в арматуре в результате ползучести и усадки бетона конструкции определяют в соответствии с
пп. 6
,
7
,
8 таблицы Р.1
.
В
п. 6 таблицы
даны указания по вычислению потерь от быстронатекающей ползучести для конструкций стендового изготовления, характерной особенностью которых является передача усилий преднапряжения на бетон в раннем возрасте последнего. Потери в арматуре здесь есть функция отношения
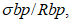
где
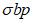 -
напряжения в бетоне на стадии передачи усилия с арматуры на бетон за вычетом уже реализовавшихся потерь по
пп. 1
-
5 таблицы Р.1
и с учетом всех нагрузок. Напряжения
-
напряжения в бетоне на стадии передачи усилия с арматуры на бетон за вычетом уже реализовавшихся потерь по
пп. 1
-
5 таблицы Р.1
и с учетом всех нагрузок. Напряжения
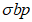 следует определять на уровне центра тяжести арматуры, для которой вычисляются потери;
следует определять на уровне центра тяжести арматуры, для которой вычисляются потери;
Rbp -
прочность бетона в момент передачи усилия с арматуры на бетон в соответствии с п. 7.3.1. Однако следует иметь в виду, что в тексте
п. 7.31
допущена опечатка. Во второй строке следует удалить предлог "не".
П.6 таблицы Р.1
рекомендуется использовать также для определения потерь в арматуре при сооружении монолитных конструкций с преднапряжением бетона на ранних сроках в том случае, если потери по
п. 6 а
превышают полученные по
п. 7.15
СП 35.
Потери предварительного напряжения в арматуре от усадки бетона приведены в
п. 7 таблицы Р.1
в виде детерминированных величин в зависимости от классов бетона на сжатие и принятой технологии создания напряжений. Нарастание этих потерь во времени так же как в случае ползучести определяется по
п. 7.15
СП 35.
Полные потери в напрягаемой арматуре от ползучести бетона за весь период существования конструкции, начиная от сооружения и до (теоретически) окончания эксплуатации предложено определять по
п. 8 таблицы Р.1
. Так же как в случае быстронатекающей ползучести полные потери в напрягаемой арматуре являются функцией отношения
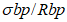 ,
но при
,
но при
 числовых коэффициентах. Полные потери от ползучести накапливаются во времени также по зависимостям, приведенным в
п. 7.15
СП 35.
числовых коэффициентах. Полные потери от ползучести накапливаются во времени также по зависимостям, приведенным в
п. 7.15
СП 35.
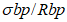 ,
но при
,
но при
 числовых коэффициентах. Полные потери от ползучести накапливаются во времени также по зависимостям, приведенным в
п. 7.15
СП 35.
числовых коэффициентах. Полные потери от ползучести накапливаются во времени также по зависимостям, приведенным в
п. 7.15
СП 35.
Для составных по длине (высоте) железобетонных конструкций с бетонируемыми стыками в
таблице Р.1
деформация одного стыка принимается постоянной и равной
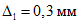 . Суммарно потери определяются по числу стыков n, приходящихся на длину пучка или его участка l, на который приходятся n стыков конструкции. Потери в арматуре вычисляются путем умножения суммы n относительных деформаций
. Суммарно потери определяются по числу стыков n, приходящихся на длину пучка или его участка l, на который приходятся n стыков конструкции. Потери в арматуре вычисляются путем умножения суммы n относительных деформаций
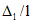 на модуль упругости напрягаемой арматуры Es.
на модуль упругости напрягаемой арматуры Es.
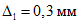 . Суммарно потери определяются по числу стыков n, приходящихся на длину пучка или его участка l, на который приходятся n стыков конструкции. Потери в арматуре вычисляются путем умножения суммы n относительных деформаций
. Суммарно потери определяются по числу стыков n, приходящихся на длину пучка или его участка l, на который приходятся n стыков конструкции. Потери в арматуре вычисляются путем умножения суммы n относительных деформаций
По
п. 10 таблицы Р.1
считается, что обжатие клеевых стыков после отверждения клея не происходит и потери в арматуре в таких конструкциях отсутствуют. Фактически это не всегда соответствует действительности. Поэтому норма
п. 10 таблицы Р.1
содержит допущение о возможности определения деформации стыков опытным путем.
Несмотря на детализированную регламентацию потерь предварительного напряжения в арматуре, приведенную в
приложении Р
СП 35, суммарное значение первых и вторых потерь не должно приниматься (в соответствии с требованием
п. 7.14
СП 35) менее 98 МПа.
7.18
СП 35.13330
регламентирует при проектировании мостовых железобетонных конструкций применение конструкционного тяжелого бетона со средней плотностью от 2200 до 2500 кг/м
3
.
В соответствии с классификацией, установленной
ГОСТ 25192-82
(СТ СЭВ 6550-88), к "конструкционному тяжелому бетону" относятся бетоны, для которых определяющими требованиями к качеству являются требования по физико-механическим характеристикам и долговечности.
Основными признаками, характеризующими "тяжелый бетон", а также "мелкозернистый бетон", указанными в тексте к
СП 35.13330
, являются бетоны на цементном вяжущем, плотных крупных и мелких заполнителях, у которых пространство между зернами крупного и мелкого или только мелкого заполнителя заполнено затвердевшим вяжущим и порами вовлеченного воздуха или газа, в том числе образующимися за счет применения добавок и регулирующих пористость в объеме не более 7%. Материалом для крупных и мелких заполнителей должны являться плотные горные породы.
Под бетонами с "другими признаками" в
СП 35.13330
подразумеваются, в частности, бетоны теплоизоляционные, жаростойкие, химические стойкие, напрягающие, ячеистые, полимербетоны, бетоны на известковых заполнителях и другие по
ГОСТ 25192-82
.
Бетон мостовых конструкций по прочности на сжатие характеризуется устанавливаемым конструктором проектным классом, обозначаемым литерой "B" и цифрой, характеризующей прочность бетона в МПа, гарантированной с обеспеченностью 0.95 (например, B30).
В зависимости от принятого для данной конструкции проектного класса значения нормативных и расчетных сопротивлений бетона в расчетах по первому и второму предельным состояниям назначаются проектировщиком в соответствии с указаниями
пп. 7.24
,
7.25
и
таблицы 7.6
СП 35.13330.
Экспериментально, в том числе при изготовлении конструкций класс бетона по прочности на сжатие определяют с использованием процедур по контролю и оценке прочности бетона, установленных
ГОСТ 18105-2010
. При этом класс бетона
B
рассчитывают по классической формуле:
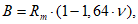
где
R
m
средние значения прочности бетона в серии стандартных образцов - кубов по
ГОСТ 10180
с учетом масштабного коэффициента принимаемого для базового размера кубов с ребром 15 см равным 1,0;
При использовании установленного
ГОСТ 26633
нормативного значения коэффициента вариации, равного 13,5%, расчет класса бетона производится по формуле:
B
= 0,78·
R
m
.
Для железобетонных конструкций нормируются 4-е вида прочности проектная, передаточная, распалубочная и отпускная.
Проектная прочность
бетона - это назначаемая в проекте прочность бетона, на момент начала эксплуатации сооружения, чаще всего в 28-суточном или другом возрасте, характеризуемая классом бетона "B".
При проектировании рекомендуется учитывать степень набора бетоном прочности при стандартных нормальных условиях твердения образцов по
ГОСТ 18105
в процентах от 28-суточной:
- 7 - 14 суток - 60 - 80%;
- 28 суток - около 100%;
- 90 суток - около 130%.
Передаточная прочность
бетона
(R
bp
)
- прочность бетона в момент передачи на него усилия от напрягаемой арматуры или других нагрузок в процессе изготовления или монтажа. В соответствии с
п. 7.31
СП 35.13330 назначается в проекте и может быть менее прочности установленного в проекте класса бетона с расчетными характеристиками, представленными в
таблице 7.6
СП 35.13330.
Отпускная прочность
бетона
(R
bo
)
- параметр сборных железобетонных, характеризующих прочность бетона на момент отгрузки конструкции со склада завода-изготовителя.
Значение отпускной прочности бетона может быть ниже проектного класса и подтверждено документацией на данную продукцию. Отпускная прочность должна обеспечивать достижение бетоном конструкции проектных значений прочности к моменту начала эксплуатации.
Класс бетона выравнивающего и защитного слоя под и над гидроизоляцией в системе дорожной одежды мостового полотна, который назначается в соответствии с указаниями
пп. 5.65
,
7.185
, должен быть не ниже B25, но не выше B27,5 и B35 соответственно для выравнивающего и защитного слоя.
Ограничение прочности бетона диктуется необходимостью обеспечить трещиностойкость выравнивающего и защитного слоя путем снижения вероятности появления усадочных и температурных трещин в процессе твердения бетона за счет снижения расхода цемента в составе бетонной смеси.
По этой же причине марку бетона слоев по морозостойкости рекомендуется назначать равной F
2
200.
При этом ограничение проектных запасов бетона по морозостойкости вполне допустимо для рассматриваемых конструктивных элементов, т.к. их эксплуатация происходит под защитой дорожного покрытия. С другой стороны, срок службы слоев до первого ремонта равен 20 годам
(ГОСТ 333178-2014)
, в течение которых количество циклов замораживания - оттаивания бетона слоев в 2,5 раза меньше, чем для бетона несущих конструкций мостов с маркой по морозостойкости F
2
300.
Следует учитывать, что повышенная прочность бетона требует дополнительных энергетических затрат при разборке слоев в процессе ремонта мостового полотна, который в плановом порядке должен проводиться каждые 10 - 20 лет.
Наконец, фактический класс бетона на сжатие по технологическим причинам, как правило, на 5,0 МПа выше проектного и значительно превышает требуемые значения прочности по несущей способности слоя
[9]
.
Для предварительно напряженных монолитных конструкций, в которых предусматривается инъецирование каналов с напрягаемой арматурой, помимо требования к цементному раствору по средней прочности на сжатие не ниже 30 МПа на 28-ой день, определенной не менее чем по трем образцам-кубам, рекомендуется указать ограничение по уменьшению объема раствора не ранее чем на 2-й день твердения в размере не более 2,0% от первоначального объема. Такое требование при производстве работ позволит технологам назначить соответствующий состав инъекционного раствора и принять соответствующие меры по обеспечению полного заполнения канала особенно в верхних зонах полигональных пучков арматуры.
7.19
Для бетонов мостовых конструкций рекомендуется применять следующую градацию проектных классов бетона по
ГОСТ 26633
:
- по прочности на сжатие: B20; B25; B30; B35; B40; B45; B50; B55; B60; B65; B70; B75; B80;
- по прочности на осевое растяжение: B
t
0,4; B
t
0,8; B
t
1,2; B
t
1,6; B
t
2,0; B
t
2,4; B
t
2,8; B
t
3,2; B
t
3,6; B
t
4,0; B
t
7,2; B
t
8,0.
Допускается применение бетона промежуточных классов по прочности на сжатие B22,5 и B27,5 при условии, что использование этих классов приводит к экономии материалов и не снижает технико-экономических показателей конструкции.
В зависимости от вида конструкций физико-механические характеристики бетона по прочности, морозостойкости и водонепроницаемости рекомендуется назначать в соответствии с
таблицами 7.4
,
7.5
СП 35.13330, а также с учетом данных
таблицы 6.1
настоящих Методических рекомендаций.
Физико-механические характеристики выравнивающего и защитного слоев бетона мостового полотна рекомендуется назначать с учетом данных
таблицы 6.1
.
Таблица 6.1
Соотношение характеристик бетона
<*>
|
Показатели
|
Марка по морозостойкости F
1
, F
2
<*>
|
Марка по водонепроницаемости, W
|
||||||
|
F
1
200 - 300
|
F
1
400 - 600
|
F
1
700 - 1000
|
6
|
8
|
10
|
12
|
14
|
|
|
F
2
100
|
F
2
200
|
F
2
300
|
||||||
|
Минимальный класс бетона, B
|
25
|
27,5
|
30
|
25
|
30
|
35
|
40
|
45
|
|
Максимальное водоцементное отношение
|
0,55
|
0,5
|
0,45
|
0,55
|
0,45
|
0,4
|
0,38
|
0,35
|
|
F
1
- не подвергающихся действию солей;
F
2
- подвергающихся действию солей.
|
||||||||
--------------------------------
Данные
таблицы 6.1
показывают, что исходя из требований по морозостойкости бетона, которая для большинства мостовых железобетонных конструктивных элементов должна быть не ниже марки F
1
200 соответствующая прочность такого бетона должна быть не ниже класса B20.
В случаях, когда необходимо обеспечить повышенную надежность конструкции, узлов и отдельных соединений (
пп. 7.28
,
7.29
) следует снижать значения коэффициентов условий работы, т.к. в этом случае восприятие внешних воздействий будет осуществлено за счет увеличения сечений, а не за счет повышения прочности материала, который имеет соответствующий разброс свойств.
При отсутствии возможности повысить надежность конструкции, например, для замкнутых сечений внутренних полостей круглых оболочек опор
(п. 7.24)
повышение надежности и несущей способности следует осуществлять за счет увеличения класса бетона.
7.20
Марка бетона по морозостойкости F назначается с учетом температур, влажности среды и воздействия растворов солей, в которых эксплуатируется железобетонная конструкция по
СП 131.13330.2012
,
СП 28.13330.2012
.
Марка бетона по морозостойкости обозначается литерой "F". Цифровой индекс "1" или "2" у литеры "F" в соответствии с действующим в настоящее время
ГОСТ 10060
указывает на отсутствие (F
1
) или возможное воздействие (F
2
) на конструкцию соляных растворов или минерализованной воды.
Марку бетона по морозостойкости фундаментов и ростверков опор путепроводов, расположенных в зонах с возможным доступом к бетону антигололедных солей с проезжей части следует назначать в соответствии с
таблицей 7.5
СП 35.13330 с обязательным обоснованием возможности такого доступа и расположения конструкции фундамента (ростверка) в зоне на глубине равной половине глубины промерзания над фундаментом.
Настоятельно не рекомендуется проводить производственный контроль морозостойкости бетона по
ГОСТ 10060
с использованием образцов, изъятых из конструкции в связи со значительными отклонениями от проектных фактических показателей бетона [
10
,
11
].
7.24
Нормативное сопротивление на сжатие R
bn
(для расчета по предельным состояниям второй группы) принимают равным призменной прочности на изгиб
R
пр
,
то есть пределу прочности призмы при разрушении, который определяется при испытании на сжатие призм размером 150 x 150 x 600 мм (или 100 x 100 x 400 мм), т.к. при отношении высоты призмы к ребру основания >= 4 трение на работу призмы не влияет. Призменная прочность больше соответствует прочности бетона на сжатие в реальных конструкциях еще и потому, что форма призмы больше напоминает конфигурацию изделий или конструкций. При испытании призмы прочность определяют делением разрушающей силы на площадь. Зависимость призменной прочности от класса можно определять по эмпирической формуле:
R
bn
= B·(0,77 - 0,001B).
Расчетное сопротивление на сжатие R
b
(для расчета по предельным состояниям второй группы) принимают равным:
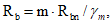
где
m
- коэффициент условий работы;
7.33
В качестве напрягаемой арматуры, имеющей непосредственное сцепление с бетоном или располагаемой в закрытых и открытых каналах, заполняемых раствором или бетоном, в железобетонных конструкциях мостов рекомендуется применять витые арматурные канаты К7 диаметром 15,2 мм и 15,7 мм по
ГОСТ 13840
и
ГОСТ Р 53772
. Допускается применение импортных канатов К7 тех же диаметров по EN 10138-3 классом не выше 1860. Основные характеристики этой арматуры приведены в
табл. 6.2
.
Таблица 6.2
ГОСТ Р 53772
и
ГОСТ 13840
|
Диаметр
|
мм
|
ГОСТ 13840
|
EN 10138-3,
ГОСТ Р 53772
|
|||||
|
15,2
|
15,3
|
15,3
|
15,2
"Компакт"
|
15,2
"Компакт"
|
15,7
|
15,7
|
||
|
Временное сопротивление разрыву,
|
МПа
|
1670
|
1770
|
1860
|
1820
|
1860
|
1770
|
1860
|
|
Номинальная площадь поперечного сечения
|
мм
2
|
139
|
140
|
140
|
165
|
165
|
150
|
150
|
|
Масса 1 м каната
|
кг
|
1,093
|
1,099
|
1,099
|
1,289
|
1,289
|
1,172
|
1,172
|
|
Допускаемое отклонение от номинальной массы
|
%
|
+/- 2
|
+/- 2
|
+/- 2
|
+/- 2
|
+/- 2
|
+/- 2
|
+/- 2
|
|
Минимальное разрывное усилие, P
u, min
|
кН
|
232
|
248
|
260
|
300
|
307
|
266
|
279
|
|
Максимальное разрывное усилие, P
u, max
|
кН
|
245
|
285
|
299
|
345
|
353
|
306
|
321
|
|
Нагрузка при условном пределе текучести
|
кН
|
197,
при
|
218
|
229
|
264
|
270
|
234
|
246
|
|
Минимальное относительное удлинение перед разрывом
|
%
|
4,0
|
3,5
|
3,5
|
3,5
|
3,5
|
3,5
|
3,5
|
|
Модуль упругости E
p
|
МПа
|
195 000
|
||||||
Применение канатов по
ГОСТ Р 53772
и EN 10138-3 рекомендуется допускать при условии проведения для поставляемых партий испытаний, предусмотренных
пп. 5.6
и
5.7
ГОСТ Р 53772. Испытания на усталостную прочность рекомендуется требовать от поставщика в случае использования этой арматуры в элементах, рассчитываемых на выносливость.
Высокопрочную проволоку гладкого или периодического профиля и стержневую арматуру по
табл. 7.14
СП 35, рекомендуется применять только в обоснованных случаях (например при наличии работоспособного оборудования) для конструкций изготавливаемых по стендовой технологии. Стальные канаты спиральные, двойной свивки, закрытые применять не рекомендуется и допускается только при технико-экономическом обосновании в сравнении с пучками из канатов К7.
В качестве арматуры без сцепления с бетоном (шпренгельной) рекомендуется применять моностренды - витые арматурные канаты К-7 в индивидуальных полиэтиленовых оболочках с антикоррозионной смазкой по СТО 71915393 - ТУ 100-2011
[16]
производства ОАО "Северсталь-метиз". Фактически это канаты по
ГОСТ Р 53772
, которые в результате дополнительного технологического передела методом экструзии заключаются в трубчатую оболочку из полиэтилена высокой плотности, которая также заполняется пластичной антикоррозионной и антифрикционной смазкой. Геометрические и весовые характеристики монострендов представлены в
таблице 6.3
.
Допускается применение импортных канатов в оболочке (монострендов) в том случае, если основу в них составляют арматурные канаты по EN 10183-3 (например известных под торговым наименованием UTIFOR от фирмы TREFILEUROPE (Франция).
Таблица 6.3
|
Диаметр каната
|
мм
|
15,3
|
15,2
Комп.
|
15,7
|
|
|
Диаметр трубки с канатом, не менее
|
мм
|
Стенка трубки 1,5 мм
|
18,3
|
18,2
|
18,8
|
|
Стенка трубки 2 мм
|
19,3
|
19,2
|
19,8
|
||
|
Масса 1 м трубки с канатом, не менее
|
кг
|
Стенка трубки 1,5 мм
|
1,218
|
1,403
|
1,303
|
|
Стенка трубки 2 мм
|
1,242
|
1,427
|
1,335
|
||
Применения в качестве рабочей напрягаемой арматуры импортных арматурных канатов, изготовленных не по нормам EN 10183-3 или отечественных, изготовленных по техническим условиям или СТО рекомендуется после исследования их физико-механических характеристик методами, предусмотренными
ГОСТ Р 53772
.
Напрягаемую арматуру из канатов К7 рекомендуется применять в виде одиночных канатов и пучков из параллельных канатов. При этом количество канатов в пучке следует назначать в увязке с типоразмерным рядом применяемых анкеров. Рекомендуемый типоразмерный ряд напрягаемых пучков из канатов К-7 приведен в таблицах
рисунков 6.1
-
6.4
наряду с другими необходимыми при проектировании физико-механическими параметрами. При этом пучки с количеством канатов К7 больше 31 следует применять в мостовых сооружениях по специально разработанным нормам.
Напрягаемая арматура всех видов и классов должна применяться в составе специально разработанных комплексных систем предварительного напряжения, элементы которых должны быть заводского изготовления и выпускаться серийно. Все элементы вновь разрабатываемых систем предварительного напряжения должны быть использованы в соответствии с требованиями ETAG 013
[17]
.
Для применения в железобетонных мостовых конструкциях может быть рекомендована система предварительного напряжения ООО "Следящие тест-системы" (СТС) элементы которой отвечают требованиям ETAG 013 и EN 13391 и выпускаются по стандарту СТО СТС 001-2017
[18]
.
На
рис. 6.1
-
6.4
приведены схемы комплектных анкеров и стыковых устройств системы ООО СТС с необходимыми для проектирования преднапряженных мостовых конструкций геометрическими параметрами в табличной форме.
Кроме того для некоторых конструктивных элементов железобетонных мостов (например для плит пролетных строений с целью их двухосного обжатия) могут быть применены арматурные элементы из 1 - 4 канатов К7 с анкерами, конструкции которых приведены на
рис. 6.5
.
7.36
В качестве неизвлекаемых каналообразователей для систем с натяжением арматуры из канатов К7 после бетонирования и с обеспечением сцепления арматуры с бетоном конструкции рекомендуется применение герметичных гофрированных труб, изготавливаемых путем вальцовки из стальной ленты толщиной 0,25 - 0,4 мм. Гофры целесообразно выполнять в виде двухзаходной резьбы, что позволяет соединять секции каналообразователя муфтами (отрезками каналообразователя длиной 250 - 300 мм большего диаметра). С системой напряжения ООО СТС (Россия) рекомендуется применять каналообразователи по ТУ 4842-005-95520222-12
[19]
. Диаметр каналообразователя следует принимать исходя из коэффициента заполнения сечения каналообразователя арматурными канатами. Отношение площади канатов в пучке к площади внутреннего поперечного сечения каналообразователя рекомендуется принимать 0,35 - 0,5. Меньшие значения этого отношения рекомендованы для длинных (> 80 м) пучков, при большем количестве (> 3) перегибов пучка, при установке пучков в каналы после бетонирования. Рекомендуемые ориентировочные диаметры каналообразователей приведены в
таблице 6.4
.
Применение оцинкованных каналообразователей, находящихся внутри бетона конструкции, запрещается из-за опасности электрохимической коррозии металла арматуры канатов, что неизбежно приведет к их обрыву под напряжением.
Таблица 6.4
для пучков из канатов К-7
|
Количество канатов в пучке, шт.
|
Рекомендуемый внутренний диаметр каналообразователя
<*>
, мм
|
Внутренний диаметр соединительной муфты, мм
|
Вес
<**>
1 пог. м каналообразователя, кг
|
|
4
|
60
|
65
|
0,57
|
|
7
|
70
|
75
|
0,67
|
|
12
|
90
|
95
|
0,86
|
|
13
|
95
|
100
|
0,91
|
|
19
|
100
|
105
|
0,96
|
|
25
|
110
|
115
|
1,06
|
|
31
|
120
|
125
|
1,16
|
--------------------------------
<*> - Для каналов до 50 м уменьшить на 5 мм, для каналов более 80 м, криволинейных увеличить на 5 мм.
Использование неизвлекаемых гофрированных полиэтиленовых каналообразователей допускается только при технико-экономическом обосновании. Одной из причин выбора полиэтиленовых каналообразователей может быть опасность блуждающих токов. При этом необходимо принимать специальные меры и для деэлектризации анкерных закреплений.
7.37
В качестве нормативного сопротивления арматурных канатов К7 по
ГОСТ 13540
следует принимать напряжения, соответствующие 95% условного предела текучести
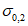 , что соответствует напряжениям в канате К7 при остаточном удлинении 0,2%. Для канатов по
ГОСТ Р 53772
как и в EN 10138-3 в качестве условного предела текучести принимается величина
, что соответствует напряжениям в канате К7 при остаточном удлинении 0,2%. Для канатов по
ГОСТ Р 53772
как и в EN 10138-3 в качестве условного предела текучести принимается величина
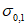 , т.е. напряжения при остаточном удлинении 0,1%. Это более жесткое требование, которое понижает нормативное сопротивление канатов и идет в запас прочности.
, т.е. напряжения при остаточном удлинении 0,1%. Это более жесткое требование, которое понижает нормативное сопротивление канатов и идет в запас прочности.
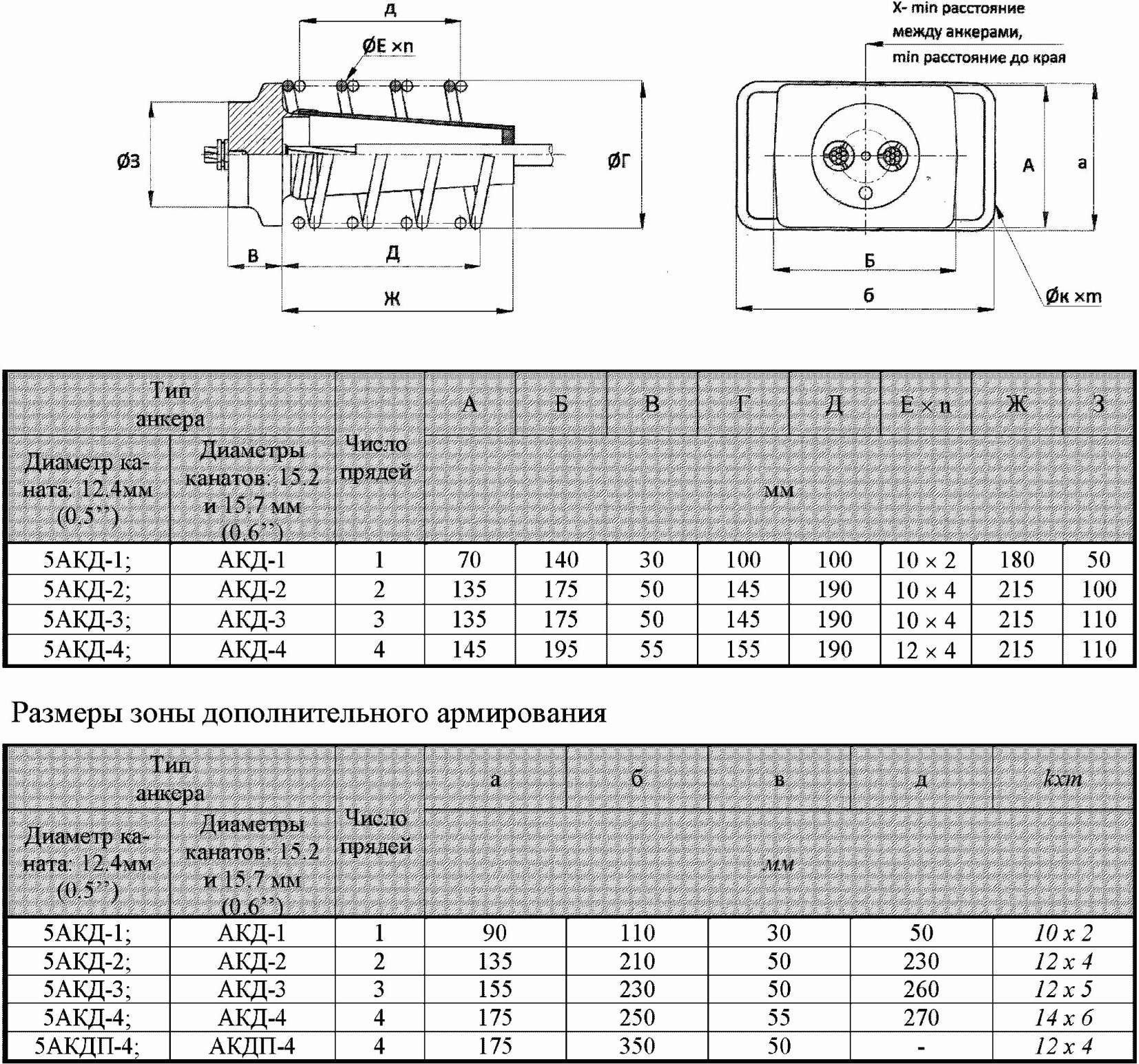
производства ООО "СТС"
Расчетные прочностные характеристики арматуры на растяжение (расчетные сопротивления) определяют, исходя из нормативных сопротивлений путем деления последних на коэффициент надежности по материалу (вида и класса арматуры (
табл. 7.15
СП 35) и умножением на коэффициент условий работы по назначению.
Как видно из
таблицы 7.15
СП 35 арматура низких классов из пластичных сталей с физическим пределом текучести имеет более низкие коэффициенты надежности по материалу (1,05 - 1,10), чем высокопрочная стержневая и проволочная арматура с условными пределами текучести (1,15 - 1,25), которые более вариабельны при производстве арматуры.
Значения коэффициентов условий работы (0,9 и 0,95) отражают разную степень обеспечения надежности конструкций по назначению (железнодорожные и автодорожные). При этом для совмещенных мостов расчетные сопротивления арматуры рекомендуется принимать как для железнодорожных при железнодорожных нагрузках и как для автодорожных - при нагрузках метро.
Для предельных состояний второй группы коэффициенты надежности по материалу и коэффициенты условий работы принимают равными 1.0, т.е. в качестве расчетных сопротивлений используют нормативные величины.
В
таблице 7.16
окончательные табличные значения расчетных сопротивлений для канатов округлены в меньшую сторону независимо от фактических значений результатов определения расчетных сопротивлений через нормативные значения.
7.38
Расчетные сопротивления арматуры сжатия принимаются равными расчетным сопротивлениям этой же арматуры растяжения, что вполне очевидно для металла. Однако на сжатие арматура способна работать только в составе железобетонного сечения, поскольку в отсутствии окружающего бетона стержневая арматура подобна сжатым стержням, способным терять устойчивость, а проволочная или канатная арматура вообще не обладает собственной жесткостью при сжатии. В связи с этим расчетные сопротивления арматуры на сжатие ограничены величинами 400 МПа при действии кратковременных нагрузок и 500 МПа при действии остальных нагрузок. Эти значения связаны с предельной сжимаемостью бетона, превышение которой ведет к его разрушению, при котором сжатая арматура теряет его поддерживающие связи, и, соответственно, способность выдерживать сжимающие нагрузки. По этой же причине расчетные сопротивления напрягаемой арматуры, не имеющей сцепления с бетоном, принимаются равными нулю.
7.39
Для расчетов на выносливость расчетные сопротивления арматуры по
п. 7.37
СП 35 следует умножать на коэффициент условий работы, зависящий от асимметрии цикла изменений напряжений в арматуре
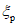 и на коэффициент
и на коэффициент
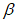 , учитывающий наличие сварных соединений и их типы.
, учитывающий наличие сварных соединений и их типы.
Значения коэффициентов
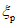 для всех видов арматуры приведены в
таблице 7.17
СП 35 и отражают физические принципы влияния переменных по знаку и величине нагрузок на длительную прочность материала. При увеличении значения коэффициента асимметрии цикла
для всех видов арматуры приведены в
таблице 7.17
СП 35 и отражают физические принципы влияния переменных по знаку и величине нагрузок на длительную прочность материала. При увеличении значения коэффициента асимметрии цикла
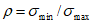 и приближении его значений к 1 влияние переменных напряжений снижается и
и приближении его значений к 1 влияние переменных напряжений снижается и
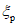 стремится к 1, а расчетные сопротивления по выносливости - к расчетным сопротивлениям по статической прочности.
стремится к 1, а расчетные сопротивления по выносливости - к расчетным сопротивлениям по статической прочности.
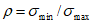 и приближении его значений к 1 влияние переменных напряжений снижается и
и приближении его значений к 1 влияние переменных напряжений снижается и
Значения коэффициентов
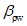 для стержневой арматуры, допускающей сварку, приведены в
таблице 7.18
и зависят от классов арматурной стали, видов сварки и коэффициента асимметрии цикла напряжений. Коэффициенты
для стержневой арматуры, допускающей сварку, приведены в
таблице 7.18
и зависят от классов арматурной стали, видов сварки и коэффициента асимметрии цикла напряжений. Коэффициенты
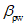 возрастают с увеличением
возрастают с увеличением
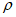 , что очевидно, поскольку при этом снижается влияние переменных нагрузок. В
таблице 7.18
отсутствуют значения
, что очевидно, поскольку при этом снижается влияние переменных нагрузок. В
таблице 7.18
отсутствуют значения
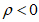 и в этих случаях предлагается принимать
и в этих случаях предлагается принимать
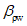 как для
как для
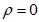 . С увеличением класса арматурной стали значения коэффициента
. С увеличением класса арматурной стали значения коэффициента
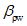 снижаются, что отражает снижение запаса пластических деформаций в сталях высокой прочности. Вместе с тем для арматуры класса А600 при контактной сварке с продольной зачисткой следует принимать
снижаются, что отражает снижение запаса пластических деформаций в сталях высокой прочности. Вместе с тем для арматуры класса А600 при контактной сварке с продольной зачисткой следует принимать
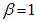 , т.е. стык без концентратора равнопрочен целому стержню.
, т.е. стык без концентратора равнопрочен целому стержню.
Для автодорожных мостов при изготовлении сварных сеток методом контактной точечной сварки из стержней диаметром 14 мм и более из стали А400 марки 25Г2С допускается увеличивать значения
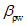 на 35% (но не более 1). При этом требуется обеспечить качество таких соединений путем разработки соответствующего технологического регламента.
на 35% (но не более 1). При этом требуется обеспечить качество таких соединений путем разработки соответствующего технологического регламента.
7.41
Следует иметь в виду, что указания этого пункта относятся уже к статической прочности арматуры при наличии ее сварных соединений.
7.42
Этот пункт отражает тот факт, что в арматуре, расположенной на удалении от наиболее растянутой грани изгибаемого элемента напряжения не достигают уровня расчетных сопротивлений, которые реализовались в наиболее загруженной нижней арматуре. Поэтому в расчет, который основан на использовании условия равенства усилий внутренней пары, усилия в менее загруженной арматуре следует вводить с уменьшенным значением.
7.43
При использовании в качестве напрягаемой арматуры канатов большого диаметра спиральной или двойной свивки в ряде случаев для их анкеровки применяли огибание канатом полукруглого блока, что приводило к перегрузке проволок во внешних слоях витого каната. Коэффициент условий работы, значения которого менее или равно 1 (при больших диаметрах огибающего устройства), призван учесть этот факт. В настоящее время такие закрепления, как и канаты двойной свивки в арматурных элементах практически не применяют.
7.45
Применение коэффициентов условий работы к расчетным сопротивлениям на 5 - 10% больше 1 для стадии создания предварительного напряжения отражает наличие запасов в напрягаемой арматуре, которые, учитывая последующее проявление потерь напряжений, целесообразно использовать.
При наличии результатов соответствующих испытаний (по
п. 7.33
) коэффициенты условий работы могут быть еще повышены, но при условии, что расчетные сопротивления с учетом этих коэффициентов не превышают 50% временного сопротивления и 100% нормативного сопротивления (условного предела текучести).
7.47
При учете модуля упругости напрягаемой арматуры для уточнения величин вытяжки, задаваемых в проектной документации, рекомендуется использовать значения модуля упругости полученного в результате испытаний образцов арматуры.
Впервые понятие категорий трещиностойкости было введено СНиП 2.03.01-84 в
п. 1.16
которого указано: "К трещиностойкости конструкций (или их частей) предъявляются требования соответствующих категорий в зависимости от условий, в которых они работают, и от вида применяемой арматуры:
а) 1-я категория - не допускается образование трещин;
б) 2-я категория - допускается ограниченное по ширине непродолжительное раскрытие трещин при условии обеспечения их последующего надежного закрытия (зажатия);
в) 3-я категория - допускается ограниченное по ширине непродолжительное и продолжительное раскрытие трещин.
Под непродолжительным раскрытием трещин понимается их раскрытие при совместном действии постоянных, длительных и кратковременных нагрузок, а под продолжительным - только постоянных и длительных нагрузок".
В
СНиП 2.05.03-84
для конструкций мостов и их частей для более полного учета специфики работы мостовых конструкций с учетом их ответственности категории трещиностойкости были разделены на подкатегории. При этом конструкции мостов, в которых от эксплуатационных нагрузок появление трещин по расчету при проектировании не допускалось, все-таки были отнесены не к 1-й, а ко 2-й (2а) категории трещиностойкости. Тем самым указывалось, что появление трещин связанных с совокупностью технологических и силовых факторов в ограниченном количестве допустимо, так как не требует остановки эксплуатации сооружения.
В этой части в
СП 35
сохранена та же идеология. Возможность появления нормальных трещин в конструкциях, отнесенных к категории 2а, подтверждается положениями
п. 7.101
.
Табл. 7.24
дополнена требования для стыков составных поперечно-члененных конструкций, не имеющих выпусков обычной арматуры, которые были отнесены к категории трещиностойкости 2а, в
примечании
указано, что для зон этих стыков должны также выполняться требования
п. 7.88
.
В
табл. 7.24
даны расчетные требования, которым должны удовлетворять части конструкций, отнесенные к той или иной категории (подкатегории) трещиностойкости. Пояснения к этим требованиям приведены в
п. 7.102
.
В силу преемственности в
табл. 7.24
также приведены конструкции (части конструкций), которые должны быть отнесены к указанным в таблице категориям. К сожалению, таблица этой части далеко не полностью отражает весь спектр применяемых в настоящее время конструктивных решений мостовых конструкций.
Например, применение в качестве арматуры коррозионностойких арматурных элементов: из нержавеющей стали, имеющих антикоррозийное покрытие, из стеклопластиков - позволяет допускать принципиально иную величину раскрытия трещин, при этом определяющим часто становятся не требования трещиностойкости, а ограничения по деформациям (жесткости). Еще один пример: отсутствие в зонах стенок напрягаемых конструкций непосредственно напрягаемых арматурных элементов, либо применение в качестве напрягаемой арматуры арматурных канатов в индивидуальных защитных оболочках (моностренды), все это позволяет отнести эти конструкции к категориям трещиностойкости с более низкими требованиями вплоть до категории 3б.
В
СП 35
даны разъяснения о том, что, если это рационально, конструкция или ее часть может быть запроектирована в соответствии с требованиями более высокой категории трещиностойкости, при этом выполнение расчетных требований, к которым она отнесена, не требуется.
Принципиальным нововведением
СП 35
по сравнению со
СНиП 2.05.03-84
является возвращение в нормы требований по обеспечению минимального армирования для железобетонных конструкций для обеспечения трещиностойкости конструкций. Величина минимального коэффициента армирования частей конструкции, где возможно появление трещин, в том числе от технологических факторов определена величиной 0,002 (0,2%). Приводятся рекомендации по определению величины коэффициента армирования, а также расположению арматуры, обеспечивающей выполнение этого требования. Обращено внимание на то, что напрягаемая арматура, расположенная в закрытых каналах, инъектируемых после натяжения, имеет ограниченное сцепление, и по этой причине ее учет при вычислении коэффициента армирования не рекомендуется.
Здесь же следует отметить, что
СП 35
не разделяет арматуру на рабочую (устанавливается по расчету) и конструктивную (устанавливается в соответствии в определенными правилами, приведенными в нормах, в том числе в
разделе
"Конструктивные требования"). Любая арматура, устанавливаемая в конструкцию, предназначена для обеспечения надежности конструкции, вне зависимости порядка ее назначения, является рабочей.
7.96
Текст пункта оставлен без изменения по сравнению со
СНиП 2.05.03-84*
, однако актуальность выполнения его требований существенно возрастает, так как в последнее время наметились существенные тенденции к использованию напрягаемой высокопрочной арматуры совместно с обычной арматурой, применяемой без преднапряжения, так называемое "смешанное" армирование.
7.97
Рассматривается ситуация, когда на стадии сооружения (монтажа) расчетные требования к конструкции ослабляют (снижают), что связано с двумя факторами: существенно меньшие за период сооружения по сравнению со сроком эксплуатации (службы) "износ" материалов конструкций (снижение характеристик свойств материалов (старение) и повреждение сечений); контроль за конструкцией в процессе сооружения, включая сдаточные обследования и испытания.
7.98
Регулирует требования к частям конструкции, сжатым на стадии эксплуатации, ограничивая растяжение в этих зонах на стадии их сооружения требованиями, соответствующими категории трещиностойкости 2а. Таким образом, в пункте реализован принцип, что для полноценной реализации прочностных свойств бетона на сжатие в процессе эксплуатации необходимо отсутствие в нем на всех предшествующих стадиях трещин. Требование представляется консервативным, так как при определенном уровне раскрытия трещин их закрытие представляется обеспеченным.
Учитывая базовые положения о том, что категории трещиностойкости конструкций назначаются в зависимости от условий, в которых они работают, и от вида применяемой арматуры, в современных условиях при назначении категорий трещиностойкости необходимо учитывать дополнительно: ответственность сооружения, воздействие окружающей среды (в том числе защита от воздействия) и регламент эксплуатации, включая мониторинг состояния (в том числе предшествующий ему мониторинг сооружения).
7.99
Указывает на то, что контролируемый уровень напряжений в конструкции обеспечивает либо отсутствие трещин, либо указывает на возможность их появления.
7.100
Задает нормативные требования по обеспечению отсутствия продольных трещин, возникающих от сжимающих напряжений на всех стадиях сооружения и эксплуатации, путем ограничения их величинами расчетных сопротивлений осевому сжатию. В нормах величины этих расчетных сопротивлений на стадии создания предварительного натяжения и монтажа указаны выше, чем на стадии эксплуатации. При этом, в период набора бетоном проектной прочности, расчетные сопротивления бетона должны соответствовать классу бетона на момент проверок трещиностойкости, включая стадию передачи усилия предварительного натяжения на бетон.
Проверки выполняются на уровне крайней сжатой фибры сечения, а также центра тяжести предварительно напряженных сечений.
7.102
Указывает, что для категорий трещиностойкости 2б и 3а трещиностойкость считается обеспеченной при обеспечении двух требований "по образованию" и "по раскрытию" трещин, причем выполнение первой из них с тем или иным уровнем "запаса" в первую очередь говорит о вероятности появления трещин, вторая непосредственно о прогнозируемой величине раскрытия. Несмотря на то, что вторая проверка, на первый взгляд, носит определяющий характер, выполнение первой проверки является обязательной.
Необходимость выполнения проверок на раскрытие трещин для категории 3а см.
комментарий к п. 7.103
.
Практически для всего диапазона отношений
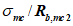 предельные значения
предельные значения
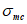 согласно
табл. 7.25
не превышают величины
согласно
табл. 7.25
не превышают величины
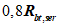 , что соответствует требованиям категории 2а и соответственно, в соответствии с
разъяснениями п. 7.95
проверка по раскрытию трещин не требуется.
, что соответствует требованиям категории 2а и соответственно, в соответствии с
разъяснениями п. 7.95
проверка по раскрытию трещин не требуется.
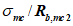 предельные значения
предельные значения
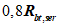 , что соответствует требованиям категории 2а и соответственно, в соответствии с
разъяснениями п. 7.95
проверка по раскрытию трещин не требуется.
, что соответствует требованиям категории 2а и соответственно, в соответствии с
разъяснениями п. 7.95
проверка по раскрытию трещин не требуется.
7.104
Выполнение требований по ограничению главных сжимающих и главных растягивающих напряжений, а также касательных напряжений нормы рекомендуют выполнять в зоне расположения центра тяжести сечения. Если в зоне центра тяжести сечения располагаются каналы для размещения пучков напрягаемой арматуры, проверяемую точку выбирают по оси канала.
Определение касательных напряжений, при этом необходимо выполнять с учетом стадийности работы сечения до омоноличивания каналов (толщины стенки за вычетом каналов) и после омоноличивания (полная толщина стенок без вычета ослаблений). В случае, если стенка наклонная, ее толщина определяется по нормали к оси стенки.
При вычислении коэффициента условий работ, учитывающего поперечное обжатие
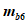 , необходимо учитывать закон парности касательных напряжений, из которого следует, что касательное напряжение в вертикальной плоскости совпадает по величине с касательным напряжением, действующим по горизонтальной площадке в той же точке, но по нормали к этой площадке обычно никакого обжатия не действует, по этой причине за исключением проверок опорных сечений этот коэффициент равен 1,0.
, необходимо учитывать закон парности касательных напряжений, из которого следует, что касательное напряжение в вертикальной плоскости совпадает по величине с касательным напряжением, действующим по горизонтальной площадке в той же точке, но по нормали к этой площадке обычно никакого обжатия не действует, по этой причине за исключением проверок опорных сечений этот коэффициент равен 1,0.
При определении поперечной силы для определения касательных напряжений, как правило, надо учитывать ее уменьшение от усилий предварительного натяжения в наклонных участках пучков, пересекающих расчетное сечение.
Нормы предписывают при определении нормальных и касательных напряжений учитывать переменность сечения по длине конструкции. Наиболее актуально это при определении поперечной силы, учитываемой при вычислении касательных напряжений. Общепризнанной методики расчета в настоящее время нет. Однако два фактора, влияющих на значение поперечной силы, общеизвестны и могут быть определены по следующей зависимости:
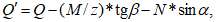
где
Q -
поперечная сила в сечении, вычисленная как первая производная от изгибающего момента;
M -
изгибающий момент в сечении, с учетом сил предварительного натяжения относительно центра тяжести сечения (положительное значение момента растягивает нижнее волокно);
z -
плечо внутренней пары сил, допускается принимать равной высоте сечения;
N -
продольное усилие, в том числе от предварительного натяжения, положительное значение соответствует сжатию;
Для балок постоянного сечения влияние переменности сечения может выражаться в учете переменности толщины нижнего и верхнего поясов.
7.105
-
7.110
Формула определения величины раскрытия трещин, полученная опытным путем О.Я. Бергом, учитывает линейную зависимость между напряжениями в арматуре растянутой зоны и величиной раскрытия трещин.
Арматура, учитываемая в расчете (арматура, воспринимающая растяжение растянутой зоны бетона), должна иметь гарантированное сцепление, а также гарантированную длину заделки в случае ее обрыва вблизи сечения. Коэффициенты, учитывающие качественные характеристики сцепления, приведены в
табл. 7.26
. Необходимо отметить, что в таблице для напрягаемой арматуры приведены значения коэффициента сцепления только для натяжения "на упоры". При натяжении на бетон эти коэффициенты будут существенно ниже. Поэтому в настоящее время пучки большой мощности в расчетах по определению величины раскрытия трещин принято не учитывать. В случае их учета можно рекомендовать коэффициент, равный 0,3 ... 0,5 и отражающий отношение числа канатов во внешнем слое пучка к общему количеству канатов в пучке.
7.117
Минимальные толщины стенок, плит, диафрагм, ребер, приведенные в
таблице 7.27
, ограничивают исходя из соображений технологичности их изготовления и долговечности (с учетом процессов деградации бетона во времени) несмотря на то, что по расчету такие толщины могут не требоваться. С учетом опыта эксплуатации в несущих элементах пролетных строений рекомендуется назначать минимальную толщину 12 см.
В
таблице 7.27
имеются опечатки:
- в
п. 2б
прочерки в столбцах, относящиеся к строке "между стенками (ребрами)" следует удалить, поскольку эта строка является заглавной к нижележащим;
- в
п. 2в
вместо "в стенках" следует читать "в плите".
7.119
Минимальные величины толщины защитного слоя назначают по
таблице 7.29
. Величины, включенные в таблицу, назначены исходя из условия исчерпания пассивирующих свойств бетона за весь срок службы элемента с учетом уровня его ответственности.
Максимальную толщину неармированного защитного слоя рекомендуется ограничивать величиной:
в плитах, ребрах, стенках пролетных строений - 5 см;
в элементах опор - 7 см.
7.121
-
7.123
Минимальные расстояния в свету в бетоне между арматурными элементами, включая каналообразователи, назначены исходя из следующих предпосылок:
- технологические требования по обеспечению заполнения бетоном всего объема конструкции, включая равномерное распределение по объему крупного заполнителя;
- обеспечение прогнозируемого сцепления арматуры с бетоном;
- обеспечение передачи усилия с напрягаемой арматуры на бетон.
При смешанном армировании минимальное расстояние между ненапрягаемым арматурным стержнем и арматурным пучком или стенкой закрытого канала по
п. 7.123
рекомендуется принимать в соответствии с указанием
п. 7.122
.
Для предварительно напряженных конструкций указания по расстояниям между армоэлементами в свету сведены в
таблицу 7.30
в зависимости от диаметра армоэлемента или канала с дополнительным ограничением абсолютной величины. Следует иметь в виду, что в
п. 4 таблицы
для канатов К7 расположенных в два ряда ошибочно указана величина 3,5 см. Следует принимать не менее 5 см.
7.124
-
7.128
Указания по анкеровке рабочей арматуры гладкого профиля следует признать морально устаревшими, как и использование подобной арматуры в качестве рабочей в новых или ремонтируемых конструкциях.
В
п. 7.127
под термином "крайние стержни" следует понимать стержни нижнего ряда, расположенные вдоль боковых граней ребра. Остальные стержни продольной арматуры, доходящие до зоны опирания балки, должны заводиться за ось опирания на длину, равную не менее чем 8 диаметрам арматуры.
7.129
-
7.132
Под прочностью анкеров, соединительных муфт, опорных закладных элементов, зон анкеровки подразумеваются усилия, которые должны воспринимать эти элементы без каких-либо разрушений. Эти усилия должны быть не менее 95% агрегатной прочности пучка (например из канатов К7). Гарантию выполнения этого положения должен давать поставщик системы преднапряжения на основании подтвержденных документально результатов испытаний. При испытаниях разрушение армоэлемента при 95% прочности должно происходить в виде разрыва отдельных канатов, без разрушения других деталей анкеровки.
Указание, что концевые анкеры на торцах балок следует, как правило, располагать равномерно рекомендуется понимать как необходимость выдерживать минимальные предлагаемые поставщиком системы преднапряжения расстояния между анкерами и от анкера до ребра опорной грани.
Армирование поперечными сетками зон обетонирования концевых анкеров не следует путать с сетками, устанавливаемыми под анкерами в основном бетоне конструкции для работы на местные напряжения.
7.135
Необходимость расположения части верхней и нижней арматуры в неразрезных балках и ригелях непрерывно по длине без обрыва или полигонального перевода из нижней зоны в верхнюю и наоборот связана с возможностью изменения эпюры моментов по величине и знаку из-за деформаций опор или процессов ползучести бетона. При этом непрерывность верхних и нижних и доля такой арматуры может быть обеспечена как за счет напрягаемой, так и стержневой ненапрягаемой арматуры или их комбинированием путем приведения одной к другой по расчетным сопротивлениям.
7.141
Требование о шаге установки продольной арматуры в стенках ненапрягаемых железобетонных балок ошибочно помещено в
подразделе
"Поперечное армирование элементов".
7.149
Конструкции, размеры и расположение сеток и спиралей для поперечного (косвенного) армирования зоны расположения анкеров напрягаемых арматурных элементов рекомендуется назначать с учетом применяемых закладных деталей (анкерных стаканов) и переходных конусов, являющихся элементами комплектной системы преднапряжения. Шаг стержней сеток 10 см можно назначать в тех зонах, где они не препятствуют установке анкерных стаканов, переходных конусов, спиралей косвенного армирования и каналообразователей.
7.150
-
7.151
Все указания по конструированию поперечного армирования в сжатых элементах конструкции направлены на обеспечение восприятия поперечной силы и удержания в бетонном сечении продольной сжатой арматуры, расположенной в углах сечения и у его боковых граней. Кроме хомутов, для этих же целей рекомендуется использовать монтажные связи, соединяющие вертикальные стержни, расположенные у противоположенных (а не "поперечных", как ошибочно указано в тексте
п. 7.151
) граней сжатого элемента.
Требование о порядке установки поперечных связей при бетонировании следует относить к технологическим и не имеющем отношения к конструированию.
7.155
Объем контроля для сварных соединений рекомендуется отнести к требованиям технологического характера и включить в соответствующий свод правил.
7.156
Указание об ограничении отношения площадей свариваемых контактной сваркой стержней величиной 1,15 фактически не может быть распространено на диаметры менее 16 мм.
В конструкциях, для которых используется состыкованная контактной сваркой арматура, рекомендуется предусматривать продольную зачистку концентраторов напряжений (грата), что позволяет повысить предел выносливости. Зачистку возможно производить только после сварки.
7.157
Дано указание о контактной сварке пересекающихся стержней в сетках в шахматном порядке. Такой прием практически не снижает жесткости сеток, но повышает прочность и выносливость входящих в сетки стержней рабочей арматуры.
7.159
Если размеры (толщина) бетонируемых монтажных стыков сборных конструкций позволяют, рекомендуется обеспечивать разбежку сварных стыков рабочей арматуры.
7.169
Рекомендуется применять пучки из 25 и 31 канатов К7 при дополнительном технико-экономическом обосновании. При этом пучки из 31 каната следует вводить в расчет как арматуру без сцепления с бетоном. Пучки с числом канатов более 31 применять в мостовых сооружениях не рекомендуется.
Соединительные устройства (куплеры) для пучков из канатов К7 должны приниматься по документации поставщиков системы преднапряжения.
7.170
Параметры неизвлекаемых гофрированных каналообразователей для арматурных пучков из канатов К-7 следует назначать по
таблице 7.31
, если в документации поставщика системы преднапряжения не приведены иные требования.
В качестве каналообразователей допускается применение специальных полимерных гофрированных труб, поставляемых в составе комплекса системы преднапряжения.
ПРИМЕР РАСЧЕТА ИЗГИБАЕМОГО ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА
КРУГЛОГО СЕЧЕНИЯ
В данном приложении производится расчет железобетонного элемента круглого сечения диаметром
D
= 800 мм из бетона класса B30. Армирование представлено 14-ю стержнями 20-го диаметра равномерно распределенными по контуру сечения. Класс армирования А400 (А-III). Радиус армирования
r
= 335 мм. Площадь сечения одного стержня
A
s
= 3,1 см
2
.
Рисунок А.1 - Сечение изгибаемого элемента
Для расчетов по первой группе предельных состояний необходимы следующие исходные данные:
расчетное сопротивление бетона B30 сжатию согласно
таблице 7.6
СП 35.13330
R
b
= 15,5 МПа;
предельная относительная деформация бетона сжатию согласно
п. 7.32
СП 35.13330
 ;
;
 ;
;
модуль упругости бетона B30 согласно
таблице 7.11
СП 35.13330
E
b
= 32500 МПа;
коэффициент приведения армирования к бетону B30, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330
n'
= 15;
расчетное сопротивление арматуры класса А400 (А-III) согласно
таблице 7.16
СП 35.13330
R
s
= 350 МПа;
предельная относительная деформация арматуры согласно
п. 7.47
СП 35.13330
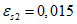 ;
;
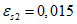 ;
;
модуль упругости арматуры согласно
таблице 7.19
СП 35.13330
E
s
= 200000 МПа;
изгибающий момент для расчетов по прочности
M
I
= 410 кНм;
изгибающий момент для расчетов по выносливости от первого загружения
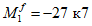 ;
;
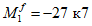 ;
;
изгибающий момент для расчетов по выносливости от второго загружения
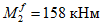 .
.
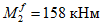 .
.
Расчет рекомендуется производить с помощью компьютерных средств.
В расчетах используются двухлинейные диаграммы деформирования бетона и арматуры.
Производится разбиение сечения по высоте на 20 участков - шаг разбивки
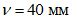 (рисунок А.2)
.
(рисунок А.2)
.
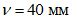 (рисунок А.2)
.
(рисунок А.2)
.
Площадь
k
-го сегмента круглого сечения
S
k
определяется по формуле:
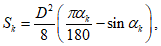 (А.1)
(А.1)
где
 - угол, охватывающий
k
-й сегмент
(рисунок А.3)
, градусы.
- угол, охватывающий
k
-й сегмент
(рисунок А.3)
, градусы.
Угол, охватывающий
k
-й сегмент
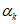 , определяется геометрически
(рисунок А.4)
:
, определяется геометрически
(рисунок А.4)
:
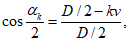 (А.2)
(А.2)
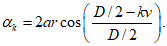 (А.3)
(А.3)
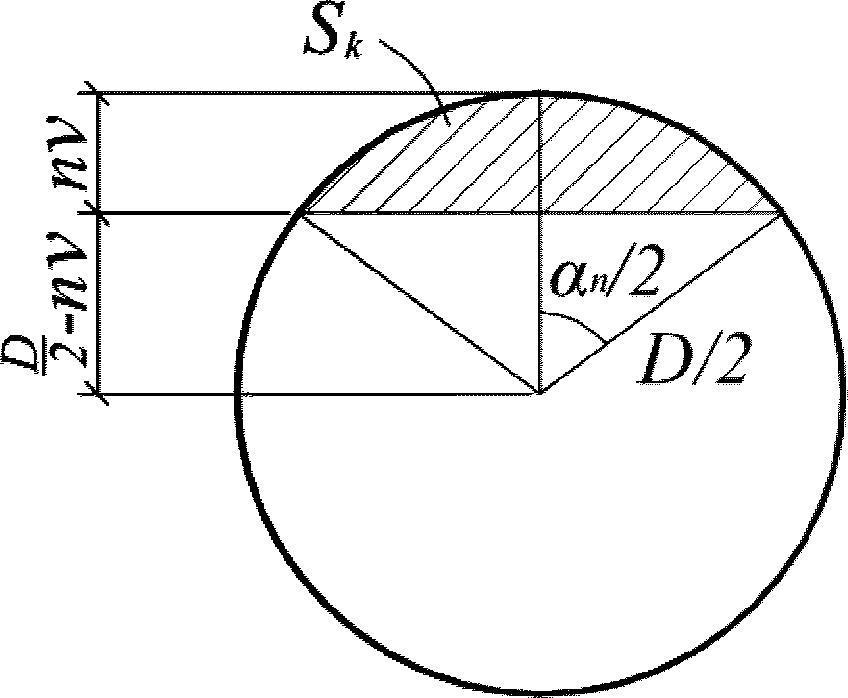
Площадь
k
-го участка вычисляется путем вычитания из площади сегмента, в котором лежит исследуемый участок
S
k
, площади сегмента, в котором лежит предыдущий участок
S
k
-1
, и определяется по формуле:
A
bk
=
S
k
-
S
k
-1
. (А.4)
Расстояние от нижней грани сечения до центра
k
-го участка
h
k
определяется по формуле
(рисунок А.5)
:
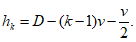 (А.5)
(А.5)
Если требуется более точный расчет, то необходимо определять расстояние от нижней грани сечения до центра тяжести
k
-го участка или производить более частую разбивку сечения.
Граничная высота сжатой зоны бетона
X
r
определяется по формуле:
 (А.6)
(А.6)
 (А.7)
(А.7)
где
a
s
min
= 0,065 м - расстояние от наиболее растянутой грани сечения до центра тяжести наиболее приближенного к ней арматурного стержня
(рисунок А.6)
.
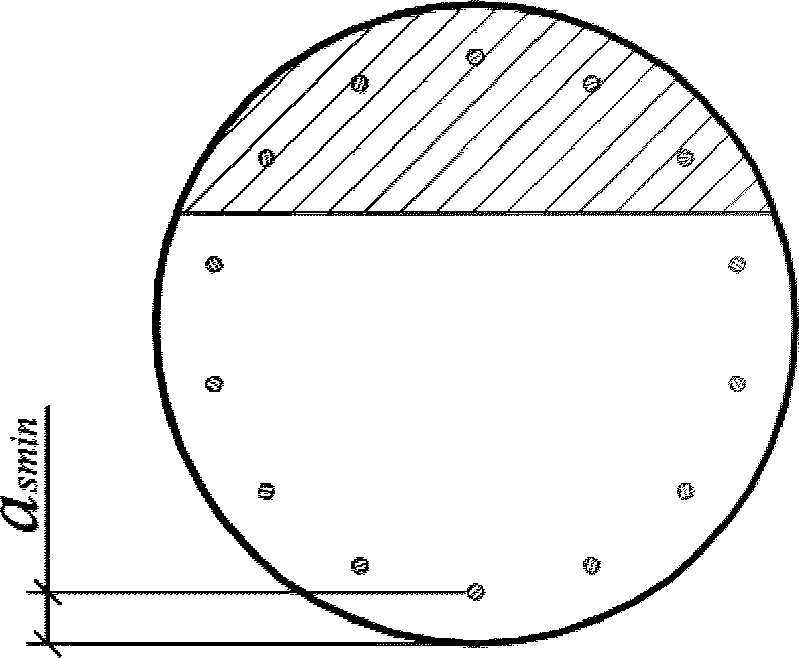
Относительные деформации
k
-го участка бетонного сечения
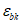 определяется по формулам:
определяется по формулам:
при
X
<=
X
r
, (А.8)
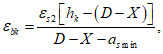 (А.9)
(А.9)
при
X
>
X
r
, (А.10)
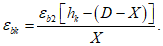 (А.11)
(А.11)
Для бетона двухлинейными диаграммами деформирования вводятся следующие условия:
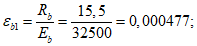 (А.12)
(А.12)
при
 , (А.13)
, (А.13)
 (А.14)
(А.14)
при
 , (А.15)
, (А.15)
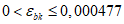 , (А.15)
, (А.15)
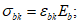 (А.16)
(А.16)
при
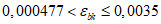 , (А.17)
, (А.17)
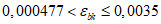 , (А.17)
, (А.17)
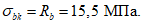 (А.18)
(А.18)
Усилия, возникающие в
k
-м участке
N
bk
, определяются по формуле:
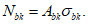 (А.19)
(А.19)
Внутренний момент, создаваемый сжатым бетоном
M
b
, определяется по формуле:
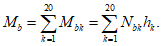 (А.20)
(А.20)
Расстояние между нижней гранью сечения и центром тяжести
i
-го арматурного стержня
a
si
допускается определять по формулам:
 (А.22)
(А.22)
В
формулах (А.21)
-
(А.23)
:
m
= 14 - количество стержней армирования.
Для арматуры двухлинейными диаграммами деформирования вводятся следующие условия:
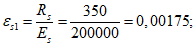 (А.24)
(А.24)
при
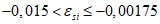 , (А.25)
, (А.25)
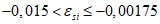 , (А.25)
, (А.25)
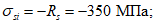 (А.26)
(А.26)
при
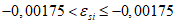 , (А.27)
, (А.27)
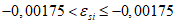 , (А.27)
, (А.27)
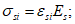 (А.28)
(А.28)
при
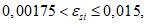 (А.29)
(А.29)
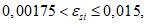 (А.29)
(А.29)
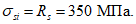 (А.30)
(А.30)
Относительные деформации
i
-го арматурного стержня
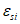 определяются по формулам:
определяются по формулам:
при
X
<=
X
r
, (А.31)
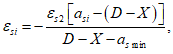 (А.32)
(А.32)
при
X
>
X
r
, (А.33)
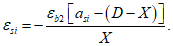 (А.34)
(А.34)
Усилия, возникающие в
i
-м ряду армирования
N
si
, определяются по формуле:
Внутренний момент, создаваемый арматурными стержнями
M
s
, определяется по формуле:
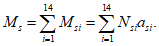 (А.36)
(А.36)
Все выше обозначенные параметры зависимы от высоты сжатой зоны бетона
X
.
Производится подбор такой высоты сжатой зоны бетона
X
, при которой соблюдается условие
(рисунок А.7)
:
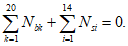 (А.37)
(А.37)
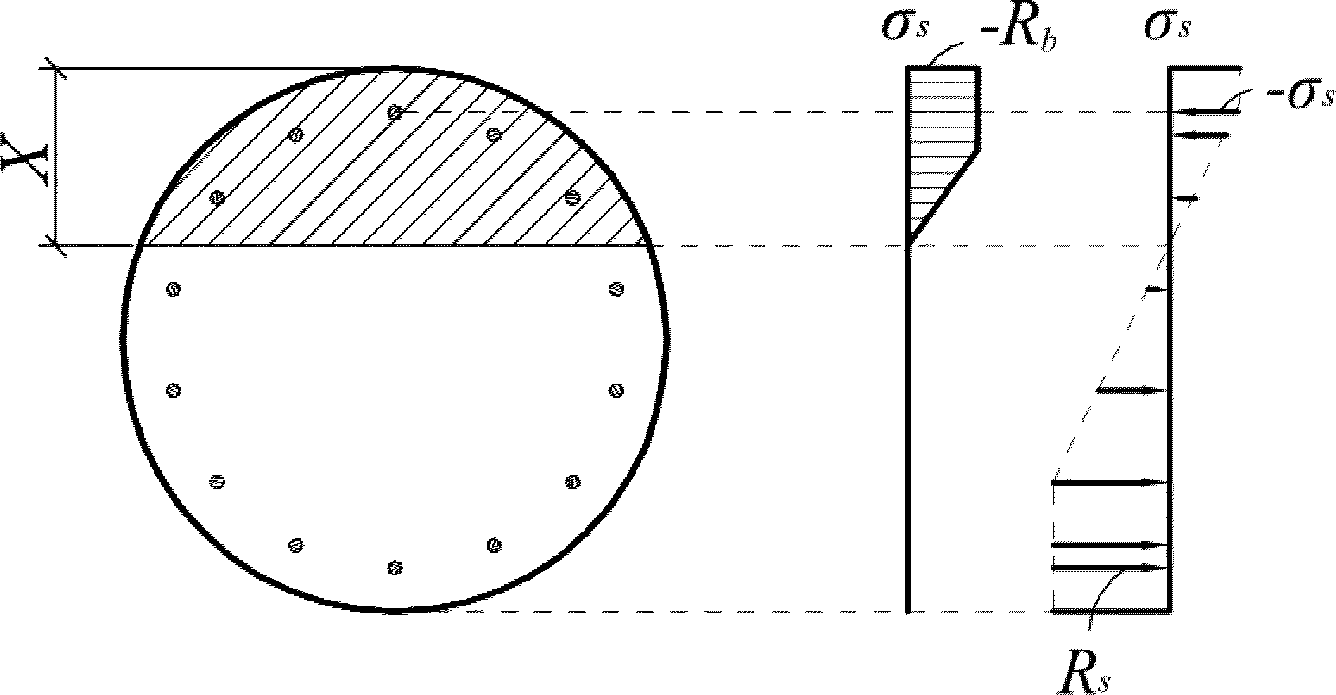
Расчеты организуются в табличном виде. Одна таблица содержит информацию для расчета параметров бетонной части сечения
(таблица А.1)
, а другая - для расчета параметров армирования
(таблица А.2)
.
|
k
|
|
S
k
|
A
bk
|
h
k
|
|
|
N
bk
|
M
bk
|
|
п/п
|
град
|
м
2
|
м
2
|
м
|
-
|
МПа
|
МН
|
МНм
|
|
1
|
51,7
|
0,00940
|
0,00940
|
0,78
|
0,00302
|
15,5
|
0,14570
|
0,11365
|
|
2
|
73,7
|
0,02612
|
0,01672
|
0,74
|
0,00207
|
15,5
|
0,25916
|
0,19178
|
|
3
|
91,1
|
0,04721
|
0,02109
|
0,7
|
0,00112
|
15,5
|
0,32690
|
0,22883
|
|
4
|
106,3
|
0,07164
|
0,02443
|
0,66
|
0,00017
|
5,5
|
0,13437
|
0,08868
|
|
5
|
120
|
0,09827
|
0,02663
|
0,62
|
-0,00079
|
0
|
0
|
0
|
|
6
|
132,8
|
0,12673
|
0,02846
|
0,58
|
-0,00174
|
0
|
0
|
0
|
|
7
|
145,1
|
0,15683
|
0,03010
|
0,54
|
-0,00269
|
0
|
0
|
0
|
|
8
|
156,9
|
0,18769
|
0,03086
|
0,5
|
-0,00364
|
0
|
0
|
0
|
|
9
|
168,5
|
0,21932
|
0,03163
|
0,46
|
-0,00460
|
0
|
0
|
0
|
|
10
|
180
|
0,25133
|
0,03201
|
0,42
|
-0,00555
|
0
|
0
|
0
|
|
11
|
191,5
|
0,28333
|
0,03200
|
0,38
|
-0,00650
|
0
|
0
|
0
|
|
12
|
203,1
|
0,31497
|
0,03164
|
0,34
|
-0,00745
|
0
|
0
|
0
|
|
13
|
214,9
|
0,34583
|
0,03086
|
0,3
|
-0,00840
|
0
|
0
|
0
|
|
14
|
227,2
|
0,37593
|
0,03010
|
0,26
|
-0,00936
|
0
|
0
|
0
|
|
15
|
240
|
0,40439
|
0,02846
|
0,22
|
-0,01031
|
0
|
0
|
0
|
|
16
|
253,7
|
0,43102
|
0,02663
|
0,18
|
-0,01126
|
0
|
0
|
0
|
|
17
|
268,9
|
0,45544
|
0,02442
|
0,14
|
-0,01221
|
0
|
0
|
0
|
|
18
|
286,3
|
0,47653
|
0,02109
|
0,1
|
-0,01317
|
0
|
0
|
0
|
|
19
|
308,3
|
0,49325
|
0,01672
|
0,06
|
-0,01412
|
0
|
0
|
0
|
|
20
|
360
|
0,50265
|
0,00940
|
0,02
|
-0,01507
|
0
|
0
|
0
|
|
Итого:
|
0,86613
|
0,62294
|
||||||
|
i
|
a
i
|
A
si
|
|
|
N
si
|
M
si
|
|
п/п
|
м
|
м
2
|
-
|
МПа
|
МН
|
МНм
|
|
1
|
0,065
|
0,00031
|
0,01400
|
350,0
|
-0,10850
|
-0,00705
|
|
2
|
0,098
|
0,00031
|
0,01321
|
350,0
|
-0,10850
|
-0,01063
|
|
3
|
0,191
|
0,00031
|
0,01100
|
350,0
|
-0,10850
|
-0,02072
|
|
4
|
0,325
|
0,00031
|
0,00781
|
350,0
|
-0,10850
|
-0,03526
|
|
5
|
0,475
|
0,00031
|
0,00424
|
350,0
|
-0,10850
|
-0,05154
|
|
6
|
0,609
|
0,00031
|
0,00105
|
210,0
|
-0,06510
|
-0,03965
|
|
7
|
0,702
|
0,00031
|
-0,00117
|
-234,0
|
0,07254
|
0,05092
|
|
8
|
0,735
|
0,00031
|
-0,00195
|
-350,0
|
0,10850
|
0,07975
|
|
9
|
0,702
|
0,00031
|
-0,00117
|
-234,0
|
0,07254
|
0,05092
|
|
10
|
0,609
|
0,00031
|
0,00105
|
210,0
|
-0,06510
|
-0,03965
|
|
11
|
0,475
|
0,00031
|
0,00424
|
350,0
|
-0,10850
|
-0,05154
|
|
12
|
0,325
|
0,00031
|
0,00781
|
350,0
|
-0,10850
|
-0,03526
|
|
13
|
0,191
|
0,00031
|
0,01100
|
350,0
|
-0,10850
|
-0,02072
|
|
14
|
0,098
|
0,00031
|
0,01321
|
350,0
|
-0,10850
|
-0,01063
|
|
Итого:
|
-0,85312
|
-0,14106
|
||||
Значения параметров
таблиц А.1
и
А.2
получены при
X
= 0,147 м.
Проверяем
условие (А.35)
:
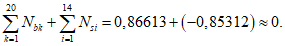 (А.38)
(А.38)
Условие соблюдается.
Расчет предельного изгибающего момента
M
ult
производится по формуле:
M
ult
=
M
b
+
M
s
= 1000[0,62294 + (- 0,14106)] =
= 481,9 кНм. (А.39)
Проверяется условие прочности:
M
I
<=
M
ult
, (А.40)
410 кНм < 481,9 кНм. (А.41)
Условие прочности соблюдается.
Расчет по выносливости производится на знакопеременные нагрузки, так как
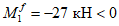 , а
, а
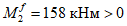 . Поэтому был бы необходим расчет геометрических характеристик нормально ориентированного сечения и обратного сечения, но так как сечение является симметричным, то производится расчет геометрических характеристик только нормально ориентированного сечения.
. Поэтому был бы необходим расчет геометрических характеристик нормально ориентированного сечения и обратного сечения, но так как сечение является симметричным, то производится расчет геометрических характеристик только нормально ориентированного сечения.
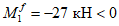 , а
, а
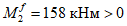 . Поэтому был бы необходим расчет геометрических характеристик нормально ориентированного сечения и обратного сечения, но так как сечение является симметричным, то производится расчет геометрических характеристик только нормально ориентированного сечения.
. Поэтому был бы необходим расчет геометрических характеристик нормально ориентированного сечения и обратного сечения, но так как сечение является симметричным, то производится расчет геометрических характеристик только нормально ориентированного сечения.
Производится подбор высоты сжатой зоны бетона
X
, при которой соблюдается условие:
где
S
B
- статический момент инерции сжатой части сечения, лежащей выше центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения, м
3
;
S
H
- статический момент инерции растянутой части сечения, лежащей ниже центра тяжести приведенного сечения и взятый относительно центра тяжести приведенного сечения, м
3
.
Ниже представлен расчет, соответствующий последней итерации, при
X
= 0,229 м.
Угол, охватывающий сжатый сегмент сечения
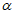 , определяется геометрически
(рисунок А.8)
:
, определяется геометрически
(рисунок А.8)
:
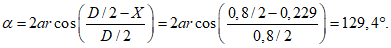 (А.43)
(А.43)
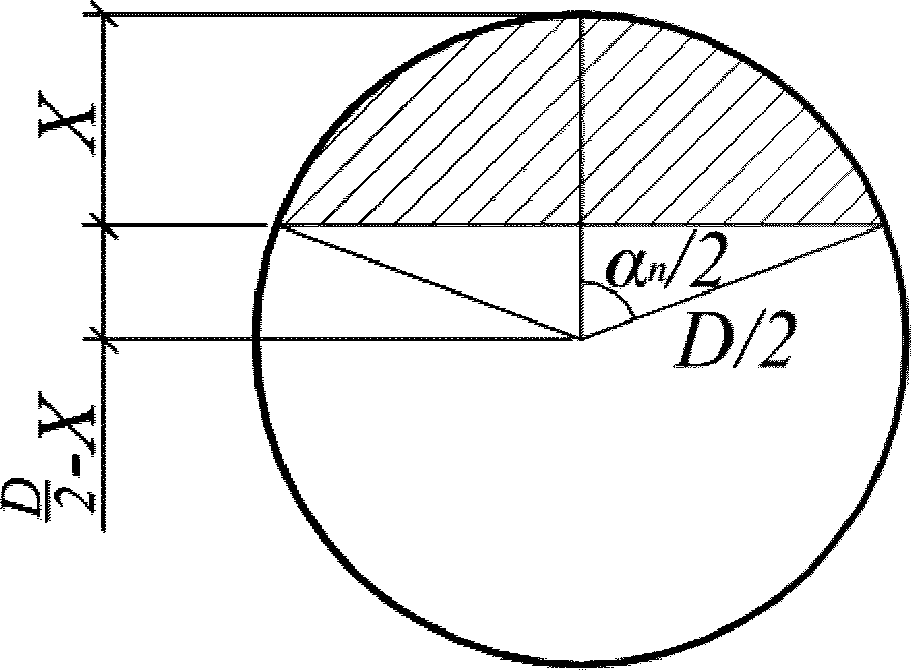
сжатый сегмент сечения
Площадь сжатой бетонной части
A
b
определяется по формуле:
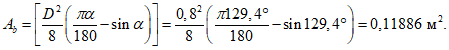 (А.44)
(А.44)
Расстояние между нижней гранью сечения и центром тяжести сжатой бетонной части
y
c
определяется по формуле
(рисунок А.9)
:
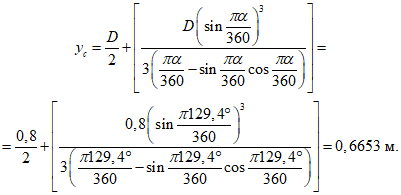 (А.45)
(А.45)
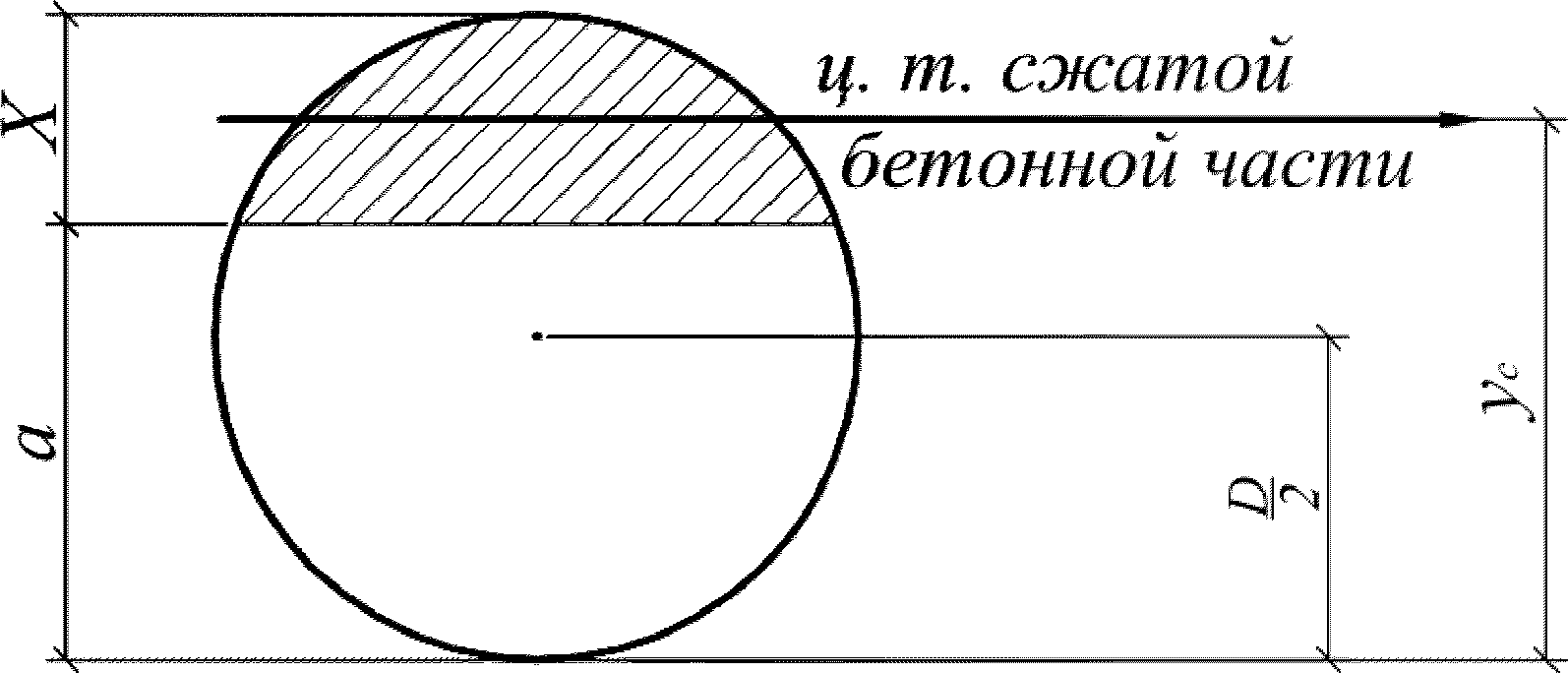
сжатой бетонной части
Статический момент инерции сжатой бетонной части
S
b
определяется по формуле:
S
b
=
A
b
(
y
c
-
D
+
X
) =
= 0,11882(0,6653 - 0,8 + 0,229) = 0,01121 м
3
. (А.46)
Расчет геометрических параметров арматурных стержней производится в табличном виде
(таблица А.3)
, исходя из следующих предпосылок:
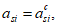 (А.48)
(А.48)
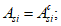 (А.49)
(А.49)
при
a
si
<
a
, (А.50)
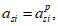 (А.51)
(А.51)
В
формулах (А.47)
-
(А.52)
:
a
si
- расстояние между нижней гранью сечения и центром тяжести
i
-го ряда армирования, м;
a
- высота растянутой зоны бетона
(рисунок А.9)
, м;
A
si
- площадь
i
-го ряда армирования, м
2
;
Расстояние между нижней гранью сечения и центром тяжести
i
-го арматурного стержня
a
si
допускается определять по
формулам А.21
-
А.23
.
Высота растянутой зоны бетона
a
определяется по формуле:
a
=
D
-
X
= 0,8 - 0,229 = 0,571 м. (А.53)
Статический момент инерции
i
-го сжатого ряда армирования, взятый относительно центра тяжести приведенного сечения
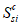 , определяется по формуле:
, определяется по формуле:
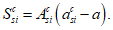 (А.54)
(А.54)
Статический момент инерции
i
-го растянутого ряда армирования, взятый относительно центра тяжести приведенного сечения
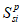 , определяется по формуле:
, определяется по формуле:
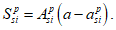 (А.55)
(А.55)
|
i
|
a
i
|
A
si
|
|
|
|
|
|
|
|
|
|
п/п
|
м
|
м
2
|
м
|
м
2
|
м
3
|
м
4
|
м
|
м
2
|
м
3
|
м
4
|
|
1
|
0,065
|
0,00031
|
-
|
-
|
-
|
-
|
0,065
|
0,00031
|
0,00016
|
0,00007937
|
|
2
|
0,098
|
0,00031
|
-
|
-
|
-
|
-
|
0,098
|
0,00031
|
0,00015
|
0,00006936
|
|
3
|
0,191
|
0,00031
|
-
|
-
|
-
|
-
|
0,191
|
0,00031
|
0,00012
|
0,00004476
|
|
4
|
0,325
|
0,00031
|
-
|
-
|
-
|
-
|
0,325
|
0,00031
|
0,00008
|
0,00001876
|
|
5
|
0,475
|
0,00031
|
-
|
-
|
-
|
-
|
0,475
|
0,00031
|
0,00003
|
0,00000286
|
|
6
|
0,609
|
0,00031
|
0,609
|
0,00031
|
0,00001
|
0,00000045
|
-
|
-
|
-
|
-
|
|
7
|
0,702
|
0,00031
|
0,702
|
0,00031
|
0,00004
|
0,00000532
|
-
|
-
|
-
|
-
|
|
8
|
0,735
|
0,00031
|
0,735
|
0,00031
|
0,00005
|
0,00000834
|
-
|
-
|
-
|
-
|
|
9
|
0,702
|
0,00031
|
0,702
|
0,00031
|
0,00004
|
0,00000532
|
-
|
-
|
-
|
-
|
|
10
|
0,609
|
0,00031
|
0,609
|
0,00031
|
0,00001
|
0,00000045
|
-
|
-
|
-
|
-
|
|
11
|
0,475
|
0,00031
|
-
|
-
|
-
|
-
|
0,475
|
0,00031
|
0,00003
|
0,00000286
|
|
12
|
0,325
|
0,00031
|
-
|
-
|
-
|
-
|
0,325
|
0,00031
|
0,00008
|
0,00001876
|
|
13
|
0,191
|
0,00031
|
-
|
-
|
-
|
-
|
0,191
|
0,00031
|
0,00012
|
0,00004476
|
|
14
|
0,098
|
0,00031
|
-
|
-
|
-
|
-
|
0,098
|
0,00031
|
0,00015
|
0,00006936
|
|
Итого:
|
0,00015
|
0,00001988
|
|
|
0,00092
|
0,00035085
|
||||
Статический момент инерции сжатой части сечения
S
B
определяется по формуле:
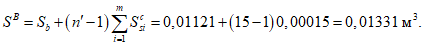 (А.56)
(А.56)
Статический момент инерции растянутой части сечения
S
H
определяется по формуле:
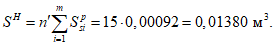 (А.57)
(А.57)
Проверяем
условие А.42
:
S
B
-
S
H
= 0,01331 - 0,01380 ~= 0. (А.58)
Собственный момент инерции сжатой бетонной части круглого сечения
I
b
0
определяется по формуле:
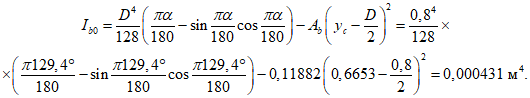 (А.60)
(А.60)
Момент инерции сжатой бетонной части сечения
I
b
, взятый относительно центра тяжести приведенного сечения, определяется по формуле:
В
формулах (А.61)
-
(А.62)
:
y
b
- расстояние между центром тяжести сжатой бетонной части и центром тяжести приведенного сечения
(рисунок А.10)
, м.
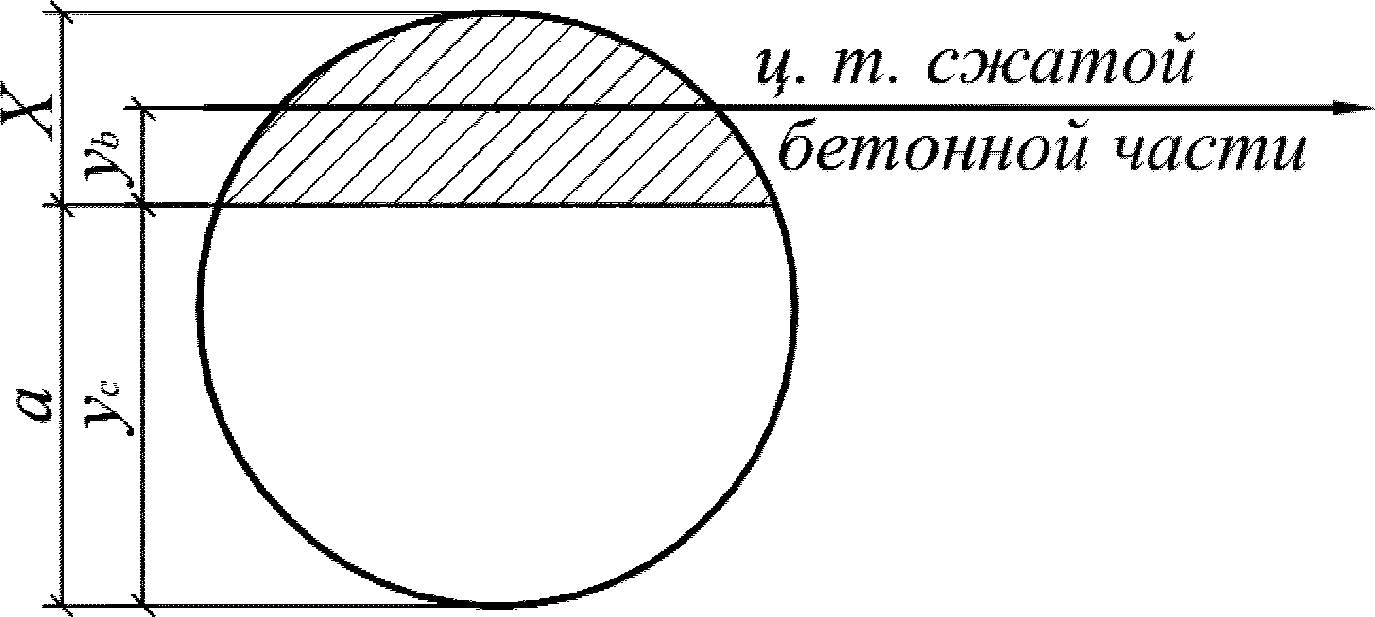
бетонной части и центром тяжести приведенного сечения
Момент инерции
i
-го сжатого ряда армирования
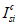 , взятый относительно центра тяжести приведенного сечения определяется по формуле
(таблица А.3)
:
, взятый относительно центра тяжести приведенного сечения определяется по формуле
(таблица А.3)
:
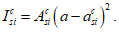 (А.63)
(А.63)
Момент инерции
i
-го растянутого ряда армирования
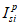 , взятый относительно центра тяжести приведенного сечения определяется по формуле
(таблица А.3)
:
, взятый относительно центра тяжести приведенного сечения определяется по формуле
(таблица А.3)
:
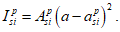 (А.64)
(А.64)
Момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения
I
red
, определяется по формуле:
Принимается, что нагрузки вызывающие сжатие верхней грани сечения, относятся к первому загружению, а нагрузки, вызывающие сжатие нижней грани сечения, относятся ко второму загружению. Поэтому теперь
 , а
, а
 .
.
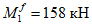 , а
, а
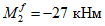 .
.
Расчет нормальных напряжений в бетоне и арматуре при знакопеременных нагрузках производится по формулам:
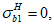 (А.67)
(А.67)
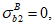 (А.68)
(А.68)
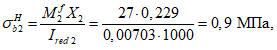 (А.69)
(А.69)
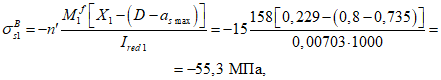 (А.70)
(А.70)
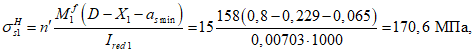 (А.71)
(А.71)
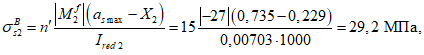 (А.72)
(А.72)
В
формулах (А.66)
-
(А.73)
:
X
1
=
X
2
=
X
= 0,229 м - высота сжатой зоны бетона нормально ориентированного сечения согласно
А.1.2.1
;
I
red
1
=
I
red
2
=
I
red
= 0,00703 м
4
- момент инерции нормально ориентированного приведенного сечения, взятый относительно центра тяжести нормально ориентированного приведенного сечения, определенный по
формуле (А.65)
;
a
s
max
- расстояние между нижней гранью сечения и центром тяжести наиболее удаленного от нее ряда армирования согласно
таблице А.3
;
a
s
min
- расстояние между нижней гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования согласно
таблице А.3
;
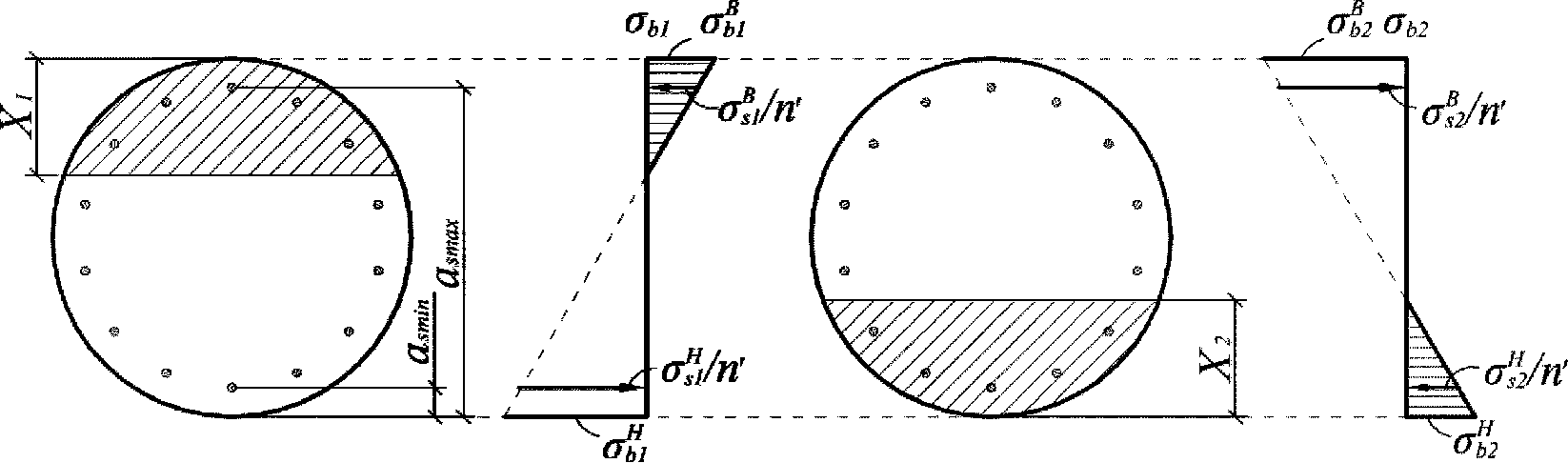
в сечении при знакопеременных нагрузках
Расчет коэффициентов асимметрии цикла для бетона и арматуры при знакопеременных нагрузках производится по формулам:
 (А.75)
(А.75)
 (А.76)
(А.76)
В
формулах (А.74)
-
(А.77)
:
Расчетные сопротивления бетона сжатию
R
bf
и арматурной стали растяжению при расчетах по выносливости при знакопеременных нагрузках определяются по формулам:
 (А.79)
(А.79)
В
формулах (А.78)
-
(А.80)
:
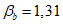 - коэффициент, учитывающий рост прочности бетона B30 во времени и принимаемый по
таблице 7.8
СП 35.13330;
- коэффициент, учитывающий рост прочности бетона B30 во времени и принимаемый по
таблице 7.8
СП 35.13330;
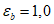 - коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в бетоне
- коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в бетоне
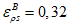 - коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в верхнем ряду армирования
- коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в верхнем ряду армирования
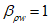 - коэффициент, учитывающий влияние на условия работы арматурных элементов наличия сварных стыков или приварки к арматурным элементам других элементов и принимаемый по
таблице 7.18
СП 35.13330 (при отсутствии сварки
- коэффициент, учитывающий влияние на условия работы арматурных элементов наличия сварных стыков или приварки к арматурным элементам других элементов и принимаемый по
таблице 7.18
СП 35.13330 (при отсутствии сварки
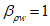 );
);
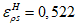 - коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в нижнем ряду армирования
- коэффициент, зависящий от асимметрии цикла повторяющихся напряжений в нижнем ряду армирования
Условия выносливости проверяются по формулам:
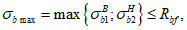 (А.81)
(А.81)
max {5,2; 0,9} = 5,2 МПа < 12,2 МПа; (А.82)
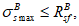 (А.83)
(А.83)
29,2 МПа < 112 МПа; (А.81)
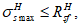 (А.82)
(А.82)
170,6 МПа < 182,7 МПа. (А.83)
Условия выносливости по бетону и арматуре соблюдаются.
Для расчетов по второй группе предельных состояний необходимы следующие исходные данные:
Сопротивление бетона B30 осевому сжатию для расчетов по предотвращению образования в конструкциях продольных трещин на стадии эксплуатации согласно
таблице 7.6
СП 35.13330
R
b
,
mc
2
= 14,6 МПа.
Нормативное сопротивление арматуры класса А400 (А-III) согласно
таблицам 7.15
и
7.16
СП 35.13330
R
sn
= 390 МПа.
Модуль упругости арматуры согласно
таблице 7.19
СП 35.13330
E
s
= 200000 МПа.
Коэффициент приведения армирования к бетону B30, учитывающий виброползучести бетона и принимаемый согласно указаниям
п. 7.48
СП 35.13330
n'
= 15.
Изгибающий момент для расчетов по второй группе предельных состояний
M
II
= 148 кНм.
Предельное значение расчетной ширины раскрытия трещин категории по трещиностойкости 3в, согласно
таблице 7.24
СП 35.13330
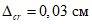 .
.
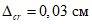 .
.
Расчет по образованию трещин заключается в ограничении нормальных сжимающих напряжений в бетоне. Для расчета напряжений предварительно необходимо вычислить геометрические характеристики сечения.
В качестве примера производится только обязательный расчет с учетом коэффициента приведения армирования к бетону
n'
согласно требованиям
п. 7.48
СП 35.13330. Расчет геометрических характеристик сечения при
n'
производился ранее согласно
А.1.2.1
.
Нормальные сжимающие напряжения в бетоне
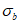 определяются по формуле
(рисунок А.12)
:
определяются по формуле
(рисунок А.12)
:
 (А.84)
(А.84)
где
X
= 0,229 м - высота сжатой зоны бетона согласно
А.1.2.1
(рисунок А.12)
;
I
red
= 0,00703 м
4
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, согласно
А.1.2.1
.
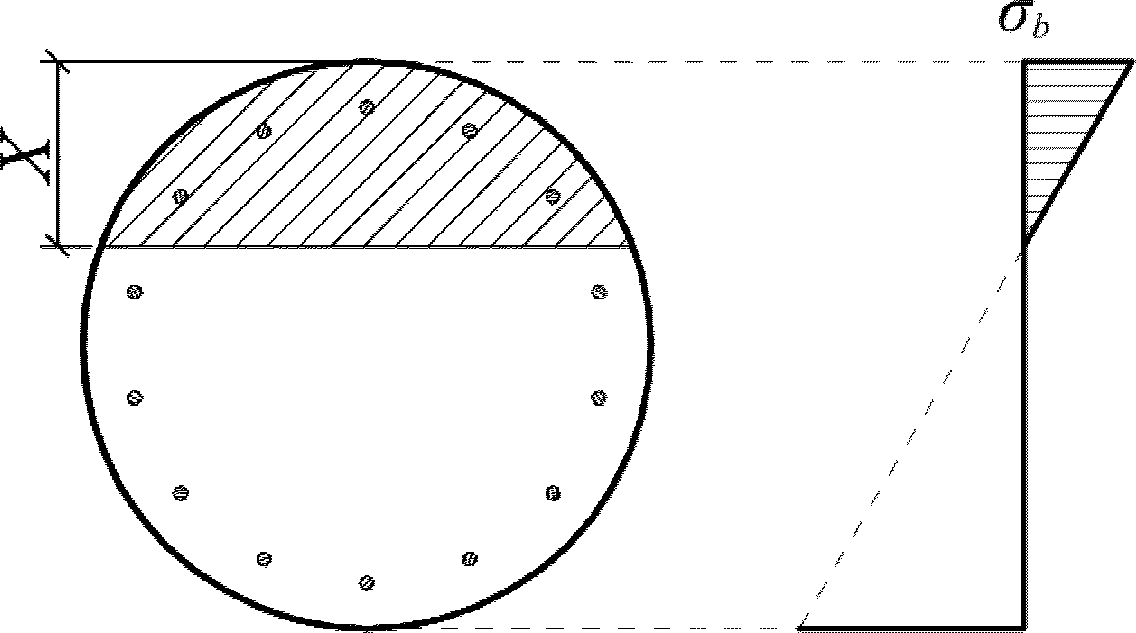
напряжений в бетоне
Ограничение нормальных сжимающих напряжений в бетоне
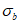 производится согласно условию:
производится согласно условию:
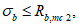 (А.85)
(А.85)
4,8 МПа < 14,6 МПа. (А.86)
Ограничение по образованию трещин выполняется.
Нормальные напряжения в наиболее растянутом ряду армирования
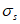 определяются по формуле:
определяются по формуле:
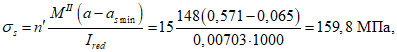 (А.87)
(А.87)
где
a
= 0,571 м - высота растянутой зоны бетона, согласно
А.1.2.1
(рисунок А.13)
;
a
s
min
= 0,065 м - расстояние между наиболее растянутой гранью сечения и центром тяжести наиболее приближенного к ней ряда армирования согласно
таблице А.3
(рисунок А.13)
;
I
red
= 0,00703 м
4
- момент инерции приведенного сечения, взятый относительно центра тяжести приведенного сечения, согласно
А.1.2.1
.

в наиболее растянутом арматурном стержне
Рисунок 3.23 - Схема к определению напряжений
в растянутой арматуре
Ограничение нормальных напряжений в наиболее растянутом ряду армирования
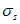 производится согласно условию:
производится согласно условию:
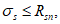 (А.88)
(А.88)
159,8 МПа < 390 МПа. (А.89)
Ограничение по напряжениям в растянутой арматуре выполняется.
В круглых сечениях площадь зоны взаимодействия
A
r
и радиус армирования
R
r
следует определять для наиболее растянутого стержня.
Сумма
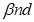 для круглого сечения с армированием из одиночных стержней, равномерно распределенных по контуру, определяется по формуле:
для круглого сечения с армированием из одиночных стержней, равномерно распределенных по контуру, определяется по формуле:
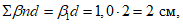 (А.90)
(А.90)
где
 - коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
- коэффициент для одиночных стержней, учитывающий степень сцепления арматурных элементов с бетоном согласно
таблице 7.26
СП 35.13330;
d
= 2 см - диаметр стержней сечения, см.
Для круглых сечений с арматурой, равномерно распределенной по контуру, радиус взаимодействия принимается
r
= 3
d
.
Площадь зоны взаимодействия для нормального сечения, ограничивается наружным контуром сечения, радиусом взаимодействия
r
и не должна выходить за пределы растянутой зоны сечения. Площадь зоны взаимодействия определяется геометрически
A
r
= 151,78 см
2
(рисунок А.14)
.
Радиус армирования
R
r
определяется по формуле:
 (А.91)
(А.91)
Для стержневой арматуры периодического профиля класса А400 коэффициент раскрытия трещин
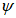 определяется по формуле:
определяется по формуле:
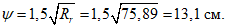 (А.92)
(А.92)
Расчетная ширина раскрытия нормальных трещин
a
cr
определяется по формуле:
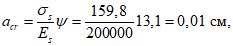 (А.93)
(А.93)
где
 - напряжения в наиболее растянутом стержне армирования согласно
А.2.2
, МПа.
- напряжения в наиболее растянутом стержне армирования согласно
А.2.2
, МПа.
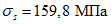 - напряжения в наиболее растянутом стержне армирования согласно
А.2.2
, МПа.
- напряжения в наиболее растянутом стержне армирования согласно
А.2.2
, МПа.
Ограничение ширины раскрытия нормальных трещин производится согласно условию:
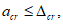 (А.94)
(А.94)
0,01 < 0,03 см. (А.95)
Условие по ограничению ширины раскрытия нормальных трещин выполняется.
1.
Р 50.1.075-2011
. Рекомендации по стандартизации. Разработка стандартов на термины и определения. М. Стандартинформ.
2.
РМГ 19-96
. Рекомендации по межгосударственной стандартизации. Рекомендации по основным принципам и методам стандартизации терминологии. Минск, 1996 г.
4.
Сборник
разъяснений требований стандартов системы проектной документации для строительства и ответы. Вып. 1.
6. Терминологический словарь по бетону и железобетону. ФГЦП "НИЦ "Строительство". М., 2007.
8.
Постановление
Правительства РФ от 15.07.2010 N 533 "Об утверждении технического регламента о безопасности высокоскоростного железнодорожного транспорта".
9. Дьяков К.А., Черсков Р.М., Зинченко Е.В., Овчинников И.Г. Проведение экспериментальных исследований по анализу влияния гидроизоляции и дорожной одежды различных типов на сопротивляемость дорожной одежды сдвиговым деформациям. Интернет ресурс. 2012 г.
10. Добшиц Л.М. Морозостойкость бетонов транспортных сооружений и пути ее повышения. Дисс. докт. техн. наук. 05.23.05 - М., 2000, - 385 с.
11. Малюк В.Д. Морозостойкость бетона транспортных искусственных сооружений, возводимых в сложных природных климатических условиях (на примере о. Сахалин): Автореферат дисс. канд. техн. наук. 05.23.05. - Днепропетровск, ДИСИ, 1984. - 23 с.
12. Руководство для проектировщиков к Еврокоду 2 EN 1992-2: Основы проектирования сооружений из железобетона. Часть 2: Железобетонные мосты: пер. с англ./К.Р. Хенди, Д.А. Смит: М.: МГСУ, 2014. 608 с.
17. ETAG 013. Guideline for European technical approval of post-tensioning kits for prestressing of structures/European Organisation for Technical Approvals. - Brussels, 2002, 136 p.
18. СТО СТС 001-2017. Система предварительного напряжения строительных конструкций арматурными прядями, работающими со сцеплением/ООО СТС. - М.: 2017, 146 с.
19. ТУ 4842-005-95520222-12. Каналообразователи металлические гофрированные/ПАО Мостотрест. - М.: 2012.
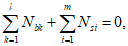
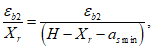
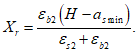
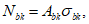
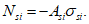
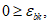 (3.10)
(3.10)
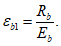
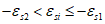 , (3.17)
, (3.17)
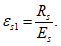
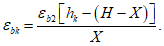
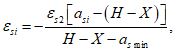
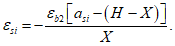
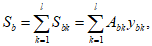
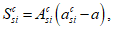

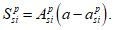
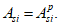
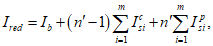
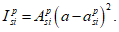
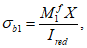
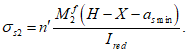
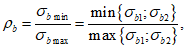
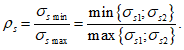
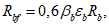
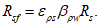
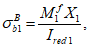
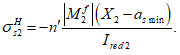
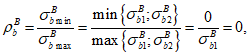
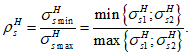
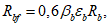
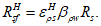
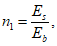
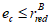 (4.1)
(4.1)
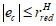 . (4.2)
. (4.2)
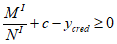 , (4.5)
, (4.5)
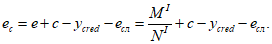
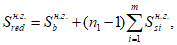
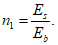
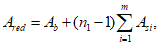
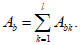
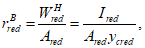
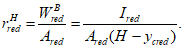
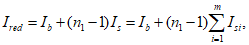
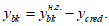
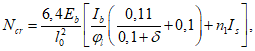
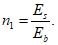
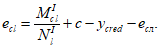
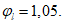
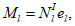
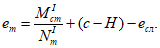
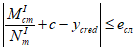 , (4.65)
, (4.65)
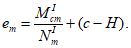
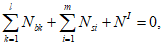
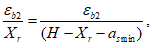
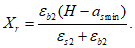
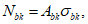
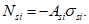
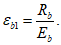
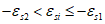 , (4.91)
, (4.91)
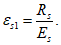
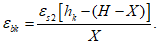
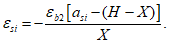
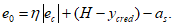
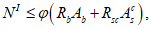
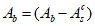
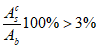 . (4.123)
. (4.123)
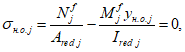
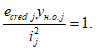
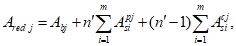
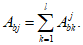
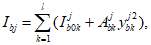
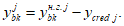
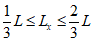 , (4.163)
, (4.163)
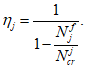
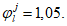
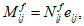
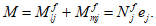
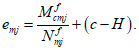
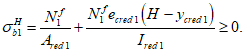
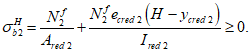
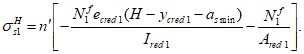
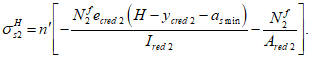
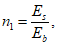
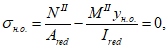
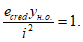
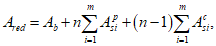
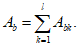
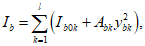
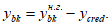
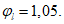
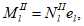
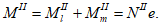
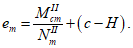
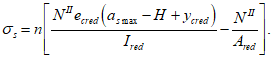
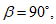 (5.2)
(5.2)
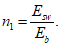
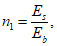
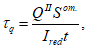
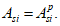
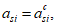
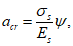
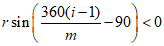 , (А.21)
, (А.21)
 . (А.23)
. (А.23)