СВЕДЕНИЯ О ДОКУМЕНТЕ
Источник публикации
М.: Минстрой России, 2023
Примечание к документу
Текст документа приведен в соответствии с публикацией на сайте https://minstroyrf.gov.ru/ по состоянию на 13.10.2023.
Документ
введен
в действие с 12.10.2023.
Название документа
"СП 529.1325800.2023. Свод правил. Определение основных расчетных гидрологических характеристик"
(утв. и введен в действие Приказом Минстроя России от 11.09.2023 N 654/пр)
"СП 529.1325800.2023. Свод правил. Определение основных расчетных гидрологических характеристик"
(утв. и введен в действие Приказом Минстроя России от 11.09.2023 N 654/пр)
Приказом
Министерства строительства
и жилищно-коммунального хозяйства
Российской Федерации
от 11 сентября 2023 г. N 654/пр
СВОД ПРАВИЛ
ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАСЧЕТНЫХ ГИДРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
Determination of the main design
hydrological characteristics
СП 529.1325800.2023
Дата введения
12 октября 2023 года
Сведения о своде правил
1 РАЗРАБОТАН Федеральным государственным бюджетным учреждением "Государственный гидрологический институт" (ФГБУ "ГГИ") Федеральной службы по гидрометеорологии и мониторингу окружающей среды (Росгидромет)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 "Строительство"
3 ПОДГОТОВЛЕН к утверждению Департаментом градостроительной деятельности и архитектуры Министерства строительства и жилищно-коммунального хозяйства Российской Федерации (Минстрой России)
4 УТВЕРЖДЕН
приказом
Министерства строительства и жилищно-коммунального хозяйства Российской Федерации от 11 сентября 2023 г. и введен в действие с 12 октября 2023 г.
5 ЗАРЕГИСТРИРОВАН Федеральным агентством по техническому регулированию и метрологии (Росстандарт)
6 ВВЕДЕН ВПЕРВЫЕ
В случае пересмотра (замены) или отмены настоящего свода правил соответствующее уведомление будет опубликовано в установленном порядке. Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте разработчика (Минстрой России) в сети Интернет
Настоящий свод правил разработан в целях обеспечения требований Федерального
закона
от 30 декабря 2009 г. N 384-ФЗ "Технический регламент о безопасности зданий и сооружений".
Свод правил разработан авторским коллективом ФГБУ "ГГИ" Росгидромета (руководитель - д-р геогр. наук
В.Ю. Георгиевский
, ответственные исполнители - д-р техн. наук
М.В. Болгов
, канд. геогр. наук
Л.С. Банщикова
,
В.В. Костко
, канд. техн. наук
А.Г. Лобанова
, канд. геогр. наук
М.Л. Марков
).
Настоящий свод правил устанавливает общие положения и требования к организации и проведению инженерных гидрологических расчетов по определению гидрологических характеристик рек и озер для обоснования проектирования новых, реконструкции действующих предприятий, зданий и сооружений для всех видов строительства и инженерной защиты территорий.
Настоящий свод правил не распространяется на определение расчетных гидрологических характеристик при изысканиях и проектировании объектов, расположенных на участках рек и озер, находящихся в зоне влияния морских приливов, на селеопасных реках.
В настоящем своде правил приведены нормативные ссылки на следующие документы:
ГОСТ 19179-73
Гидрология суши. Термины и определения
СП 38.13330.2018
"СНиП 2.06.04-82* Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов)" (с изменением N 1)
СП 47.13330.2016
"СНиП 11-02-96 Инженерные изыскания для строительства. Основные положения" (с изменением N 1)
СП 482.1325800.2020
Инженерно-гидрометеорологические изыскания для строительства. Общие правила производства работ
Примечание - При пользовании настоящим сводом правил целесообразно проверить действие ссылочных документов в информационной системе общего пользования - на официальном сайте федерального органа исполнительной власти в сфере стандартизации в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего свода правил в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде стандартов.
В настоящем своде правил применены термины по
ГОСТ 19179
, а также следующие термины с соответствующими определениями:
3.1
водохозяйственный год:
Расчетный годичный период, начинающийся с самого многоводного сезона.
3.2
гидрологические характеристики:
Количественные оценки элементов гидрологического режима.
3.3
интенсивность дождя:
Слой осадков (в миллиметрах), выпадающих за единицу времени.
3.4
интенсивность снеготаяния:
Количество воды (в миллиметрах), образующееся в процессе таяния снега в единицу времени.
3.5
клетчатка вероятностей:
Специальные клетчатки с прямоугольной системой координат, построенные таким образом, что на них спрямляются (полностью или частично) различные кривые обеспеченности.
3.6
коэффициент редукции:
Коэффициент, характеризующий интенсивность изменения (убывания) какого-либо одного значения с изменением другого связанного с ним значения.
3.7
лимитирующий период:
Часть водохозяйственного года, неблагоприятная для осуществления проектируемых мероприятий либо по водопотреблению и водопользованию, либо по борьбе с наводнениями и осушению болот.
3.8
гидрологические расчеты:
Методы инженерной гидрологии, позволяющие рассчитать значения различных характеристик гидрологического режима.
3.9
нелимитирующий период:
Часть водохозяйственного года за вычетом лимитирующего периода.
3.10
подпор воды:
Повышение уровня воды из-за наличия в русле препятствия для ее движения.
3.11
расчетная обеспеченность:
Обеспеченность гидрологической характеристики, принимаемая при строительном проектировании для установления значения параметров гидрологического режима, определяющих проектные решения.
3.12
расчетный расход воды:
Расход воды заданной вероятности превышения, принимаемый в качестве исходного значения для определения размеров проектируемых сооружений.
3.13
редукция интенсивности дождя:
Изменение средней интенсивности дождя с увеличением его продолжительности.
3.14
редукция максимального модуля стока:
Изменение максимального модуля стока с увеличением площади водосбора.
3.15
соответственные уровни воды:
Уровни воды на двух гидрологических постах, относящиеся к одинаковым фазам уровенного режима, - гребням резко выраженных подъемов или самым низким точкам.
3.16
уклон водной поверхности:
Отношение разности отметок уровня воды на рассматриваемом участке к длине этого участка.
4.1 Настоящий свод правил содержит основные методы расчета средних годовых, максимальных и минимальных расходов воды, внутригодового распределения стока, объемов и гидрографов стока весеннего половодья и дождевых паводков, уровней воды рек и озер.
При применении других методов расчетов, не включенных в настоящий свод правил, следует провести анализ, включающий сравнительную оценку погрешностей расчета с результатами расчетов по методам, изложенным в настоящем своде правил.
4.2 Определение расчетных гидрологических характеристик основывается на данных гидрометеорологических наблюдений и их обобщениях, опубликованных в официальных документах Росгидромета, включая данные последних лет наблюдений, а также на данных наблюдений, содержащихся в архивах Единого государственного фонда данных, изыскательских, проектных организаций. Рекомендуется использовать в качестве справочных данные наблюдений за гидрологическими характеристиками по архивным, опубликованным материалам, относящимся к периоду до начала регулярных наблюдений. При этом необходимо указать источник, на основании которого установлена гидрологическая информация.
4.3 Гидрологические расчеты в случаях их выполнения на недостаточно изученной или неизученной в гидрологическом отношении территории проводят на основе материалов инженерно-гидрометеорологических изысканий, выполненных в соответствии с
СП 47.13330
,
СП 482.1325800
.
Учет кратковременных данных осуществляют методами, изложенными в
разделе 6
.
4.4 Данные гидрометрических наблюдений следует подвергать проверке, включающей анализ:
- полноты и надежности наблюдений за уровнями и расходами воды;
- наличия данных о высших (мгновенных и среднесуточных) и низших уровнях воды за время наблюдений при свободном ото льда русле, ледяном покрове, ледоходе, заторе льда, заросшем водной растительностью русле, подпоре от нижерасположенной плотины, сбросах воды выше гидрометрического створа, полноты учета стока воды на поймах и в протоках;
- обоснованности экстраполяции кривых расходов воды до наивысших и наинизших уровней, а также точности расчета стока по кривым расходам за год, сезон, месяц, сутки;
- влияния хозяйственной деятельности на речной сток.
4.5 Для рек, в бассейнах которых ведется интенсивная хозяйственная деятельность, существенно нарушающая естественный гидрологический режим рек, определение расчетных гидрологических характеристик проводят по двум расчетным схемам.
Первая расчетная схема предполагает приведение гидрологических рядов наблюдений к естественным однородным стационарным условиям водно-балансовыми и регрессионными методами. В расчетное значение гидрологической характеристики, полученной по естественному ряду в соответствии с
разделами 5
-
7
настоящего свода правил, вводят поправку на влияние хозяйственной деятельности. Численное ежегодное значение поправки представляет собой разность между бытовым и естественным стоками. Значение поправки расчетной вероятности превышения определяют по кривой распределения поправок.
Во второй расчетной схеме гидрологические ряды наблюдений приводят к бытовому стоку за весь период наблюдений в предположении, что сложившийся комплекс хозяйственной деятельности действовал с начала наблюдений. Восстановление бытового стока за весь период наблюдений проводят водно-балансовыми и регрессионными методами. Восстановленный ряд проверяют на однородность с использованием генетических и статистических методов. Определение расчетных гидрологических характеристик в этом случае проводят по данным за весь период наблюдений без введения поправок на хозяйственную деятельность методами, изложенными в настоящем своде правил.
Приведение речного стока к естественным условиям не проводят, если суммарное значение его изменений не выходит за пределы случайной средней квадратической погрешности исходных данных наблюдений.
Методология предлагаемых двух расчетных схем может быть применена для расчетов основных гидрологических характеристик с учетом влияния возможного регионального антропогенного изменения климата.
4.6 Определение расчетных гидрологических характеристик следует проводить по однородным рядам наблюдений. Оценку однородности рядов гидрологических наблюдений осуществляют на основе статистического анализа исходных данных наблюдений и условий формирования речного стока, обусловливающих неоднородность исходных данных наблюдений. Для количественной оценки статистической однородности применяют критерии резко отклоняющихся экстремальных значений в эмпирическом распределении (критерии Смирнова-Граббса и Диксона), критерии однородности выборочных дисперсий (критерий Фишера) и выборочных средних (критерий Стьюдента).
Критические значения статистик критериев однородности с учетом автокорреляции между смежными членами анализируемой последовательности и асимметрии эмпирического распределения приведены в приложении А (
таблицы А.1
-
А.16
).
4.7 Вероятности превышения расчетных гидрологических характеристик для каждого вида строительства устанавливают нормативными документами.
4.8 При использовании нескольких независимых (не более трех) методов расчета окончательное расчетное значение рассматриваемой гидрологической характеристики
g
определяют по формуле
где
q
i
- значение рассматриваемой гидрологической характеристики, определенное различными методами;
k
- число методов.
- однотипность стока реки-аналога и исследуемой реки;
- географическая близость расположения водосборов;
- однородность условий формирования стока, сходство климатических условий, однотипность почв (грунтов) и гидрогеологических условий, близкая степень озерности, залесенности, заболоченности и распаханности водосборов;
- средние высоты водосборов не должны существенно отличаться; для горных и полугорных районов следует учитывать экспозицию склона и гипсометрию;
- отсутствие факторов, существенно искажающих естественный речной сток (регулирование стока, сбросы воды, изъятие стока на орошение и другие нужды).
Гидрологические расчеты для проектируемого сооружения при наличии действующих сооружений на реках должны учитывать возможность их влияния и, при необходимости, предусматривать согласованные решения по совместной работе вновь проектируемых, строящихся и существующих сооружений с учетом возможности реконструкции существующих сооружений.
4.10 При проектировании водохозяйственных объектов допускается использование стохастических моделей колебаний стока рек, позволяющих моделировать искусственные ряды гидрометеорологических характеристик требуемой продолжительности. В качестве модели многолетних колебаний стока используют простую цепь Маркова.
Моделирование рядов сезонных (месячных) значений стока осуществляют на основе периодических стохастических моделей различной степени сложности. При наличии продолжительных рядов наблюдений допускается использование метода фрагментов с учетом зависимости внутригодового распределения стока от водности года.
4.11 При разработке эмпирических зависимостей и формул для применения в гидрологических расчетах при наличии, недостаточности и отсутствии данных наблюдений оценку их эффективности выполняют на основе проверки их параметров и коэффициентов на зависимом и независимом от расчетов материалах наблюдений.
5 Определение расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений
5.1.1 Определение расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений достаточной продолжительности осуществляют путем применения аналитических функций распределения ежегодных вероятностей превышения - кривых обеспеченностей.
Продолжительность периода наблюдений считают достаточной, если рассматриваемый период репрезентативен, а относительная средняя квадратическая погрешность расчетного значения исследуемой гидрологической характеристики не превышает 10% для годового и сезонного стоков и 20% - для максимального и минимального стоков.
Если относительные средние квадратические погрешности превышают указанные пределы и период наблюдений нерепрезентативен, необходимо осуществить приведение рассматриваемой гидрологической характеристики к многолетнему периоду согласно
разделу 6
.
Средние квадратические погрешности расчетного значения исследуемой гидрологической характеристики устанавливают по
формулам (5.25)
-
(5.29)
или по таблицам, полученным методом статистических испытаний.
5.1.2 Эмпирическую ежегодную вероятность превышения гидрологических характеристик определяют по формуле
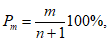 (5.1)
(5.1)
где
m
- порядковый номер членов ряда гидрологической характеристики, расположенных в убывающем порядке;
n
- общее число членов ряда.
5.1.3 Для сглаживания и экстраполяции эмпирических кривых распределения ежегодных вероятностей превышения применяют трехпараметрические распределения: Крицкого-Менкеля при любом отношении
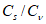 , распределение Пирсона III типа (биномиальная кривая) при
, распределение Пирсона III типа (биномиальная кривая) при
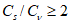 (приложение Б)
, лог-нормальное распределение при
(приложение Б)
, лог-нормальное распределение при
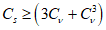 и другие распределения, имеющие предел простирания случайной переменной от нуля или положительного значения до бесконечности. При обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение
и другие распределения, имеющие предел простирания случайной переменной от нуля или положительного значения до бесконечности. При обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение
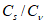 и аналитическое отношение
и аналитическое отношение
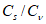 , свойственные данной функции распределения, приблизительно равны. При неоднородности ряда гидрометрических наблюдений (различные условия формирования стока) применяют усеченные и составные кривые распределения вероятностей.
, свойственные данной функции распределения, приблизительно равны. При неоднородности ряда гидрометрических наблюдений (различные условия формирования стока) применяют усеченные и составные кривые распределения вероятностей.
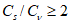 (приложение Б)
, лог-нормальное распределение при
(приложение Б)
, лог-нормальное распределение при
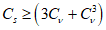 и другие распределения, имеющие предел простирания случайной переменной от нуля или положительного значения до бесконечности. При обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение
и другие распределения, имеющие предел простирания случайной переменной от нуля или положительного значения до бесконечности. При обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение
5.1.4 Оценки параметров аналитических кривых распределения: среднее многолетнее значение
 , коэффициент вариации
, коэффициент вариации
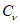 и отношение коэффициента асимметрии к коэффициенту вариации
и отношение коэффициента асимметрии к коэффициенту вариации
 устанавливают по рядам наблюдений за рассматриваемой гидрологической характеристикой методом приближенно наибольшего правдоподобия и методом моментов.
устанавливают по рядам наблюдений за рассматриваемой гидрологической характеристикой методом приближенно наибольшего правдоподобия и методом моментов.
5.1.5 Коэффициент вариации
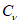 и коэффициент асимметрии
C
s
для трехпараметрического гамма-распределения Крицкого-Менкеля следует определять методом приближенно наибольшего правдоподобия в зависимости от статистик
и коэффициент асимметрии
C
s
для трехпараметрического гамма-распределения Крицкого-Менкеля следует определять методом приближенно наибольшего правдоподобия в зависимости от статистик
 и
и
 , вычисляемых по формулам:
, вычисляемых по формулам:
 (5.2)
(5.2)
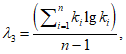 (5.3)
(5.3)
где
k
i
- модульный коэффициент рассматриваемой гидрологической характеристики, определяемый по формуле
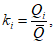 (5.4)
(5.4)
здесь
Q
i
- погодичные значения расходов воды;
 (5.5)
(5.5)
5.1.6 Коэффициенты вариации и асимметрии определяют методом моментов по формулам:
где
a
1
, ...,
a
6
;
b
1
, ...,
b
6
- коэффициенты, определяемые по
таблице В.1
, для распределения Пирсона III типа;
При
 и
C
s
< 1,0 коэффициенты вариации и асимметрии допускается определять по
формулам (5.8)
и
(5.9)
без введения поправок.
и
C
s
< 1,0 коэффициенты вариации и асимметрии допускается определять по
формулам (5.8)
и
(5.9)
без введения поправок.
 и
C
s
< 1,0 коэффициенты вариации и асимметрии допускается определять по
формулам (5.8)
и
(5.9)
без введения поправок.
и
C
s
< 1,0 коэффициенты вариации и асимметрии допускается определять по
формулам (5.8)
и
(5.9)
без введения поправок.
5.1.7 Расчетные значения отношения коэффициента асимметрии к коэффициенту вариации, а также коэффициента автокорреляции между стоком смежных лет
r
(1) следует принимать как среднее из значений, установленных по данным группы рек с наиболее продолжительными наблюдениями за рассматриваемой гидрологической характеристикой в гидрологически однородном районе с учетом площадей водосборов и других азональных факторов. Для проверки однородности эмпирических оценок
 и
r
(1) используют случайные погрешности оценок параметров по специальным таблицам, полученным методом статистических испытаний, или по аналитическим формулам. Если рассеяние эмпирических оценок
и
r
(1) используют случайные погрешности оценок параметров по специальным таблицам, полученным методом статистических испытаний, или по аналитическим формулам. Если рассеяние эмпирических оценок
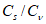 и
r
(1) больше теоретического, то принятый район признают неоднородным и он должен быть уменьшен до размеров, при которых рассеяние эмпирических оценок и теоретические погрешности будут приблизительно равны.
и
r
(1) больше теоретического, то принятый район признают неоднородным и он должен быть уменьшен до размеров, при которых рассеяние эмпирических оценок и теоретические погрешности будут приблизительно равны.
5.1.8 Уточнение параметров распределений гидрологических характеристик осуществляют методом объединения данных наблюдений по группе станций (постов) в пределах однородных районов. Рассматриваемая гидрологическая характеристика должна быть приведена к единым условиям формирования в однородном гидрологическом районе. Оценка гидрологической характеристики, приведенной к единым условиям формирования, является случайной величиной, распределение которой определяется объемом независимой информации.
Это распределение, называемое выборочным, в гидрологических расчетах характеризуется двумя его параметрами: средним значением и средним квадратическим отклонением.
5.1.9 Рассеяние оценок, вызванное ограниченностью данных наблюдений, обозначают через
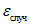 , а рассеяние, обусловленное неустраненными различиями между водосборами, - через
, а рассеяние, обусловленное неустраненными различиями между водосборами, - через
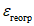 . Полная дисперсия оценки
. Полная дисперсия оценки
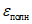 состоит из двух компонентов:
состоит из двух компонентов:
Полную дисперсию оценки
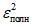 определяют по формуле
определяют по формуле
где
i
- индекс (номер) объекта. Под объектом понимают либо водосборный бассейн, либо метеорологическую станцию;
k
- число совместно анализируемых объектов;
A
i
- оценка рассматриваемого параметра по
i
-му объекту;
Случайную составляющую дисперсии оценок
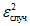 вычисляют путем осреднения дисперсий оценок этих параметров по теоретическим формулам, полученным для отдельных объектов
(5.25)
-
(5.29)
, или по результатам статистических испытаний.
вычисляют путем осреднения дисперсий оценок этих параметров по теоретическим формулам, полученным для отдельных объектов
(5.25)
-
(5.29)
, или по результатам статистических испытаний.
Географическую составляющую рассеяния
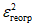 определяют по
(5.10)
как разность между полной и случайной дисперсиями. Если оценка
определяют по
(5.10)
как разность между полной и случайной дисперсиями. Если оценка
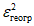 имеет отрицательный знак, то ее принимают равной нулю.
имеет отрицательный знак, то ее принимают равной нулю.
Дисперсию результата совместного расчета определяют по формуле
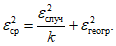 (5.12)
(5.12)
Соотношение между случайной и географической составляющими определяет состав бассейнов (объектов), обрабатываемых методом группового анализа. При увеличении числа совместно анализируемых водосборов величина случайной составляющей ошибки уменьшается. Географическая составляющая увеличивается за счет вовлечения водосборов, расположенных в пределах более обширной географической области, условия формирования стока которых различаются более существенно. Допустимым (приемлемым) следует считать число водосборов, при котором географическая составляющая не превосходит случайную:
Результатом группового анализа является оценка параметра по совокупности собственных и объединенных наблюдений в виде средневзвешенного по точности каждой из оценок:
Стандартную ошибку такой оценки рассчитывают по формуле
Для оценок асимметрии и коэффициентов автокорреляции результатом группового анализа является средняя из всех индивидуальных оценок в пределах однородного района.
5.1.10 Групповой анализ (с учетом пространственной скоррелированности данных наблюдений) выполняют в следующем порядке:
- по каждому водосбору определяют параметры распределения гидрологических характеристик, используемые для совместного анализа и необходимые для вычисления стандартных погрешностей параметров по
формулам (5.26)
,
(5.29)
;
- по каждой паре водосборов оценивают коэффициенты межрядной корреляции
R
ij
(
x
);
- по выборке величин
A
i
оценивают среднее значение параметра:
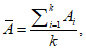 (5.16)
(5.16)
и полную дисперсию
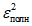 по
формуле (5.11)
;
по
формуле (5.11)
;
- определяют значения коэффициентов корреляции
R
ij
(
A
) между оценками параметра
A
по теоретическим зависимостям
(таблица В.2)
;
- определяют стандартное отклонение
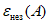 оценок параметра
A
по выборкам объема
n
, характеризующее рассеяние оценок для случая независимых выборок и определяемое по
формулам (5.26)
,
(5.29)
;
оценок параметра
A
по выборкам объема
n
, характеризующее рассеяние оценок для случая независимых выборок и определяемое по
формулам (5.26)
,
(5.29)
;
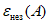 оценок параметра
A
по выборкам объема
n
, характеризующее рассеяние оценок для случая независимых выборок и определяемое по
формулам (5.26)
,
(5.29)
;
оценок параметра
A
по выборкам объема
n
, характеризующее рассеяние оценок для случая независимых выборок и определяемое по
формулам (5.26)
,
(5.29)
;
- стандартное отклонение параметра
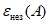 , характеризующее независимые выборки, корректируют на величину, учитывающую влияние корреляции между объединяемыми объектами:
, характеризующее независимые выборки, корректируют на величину, учитывающую влияние корреляции между объединяемыми объектами:
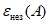 , характеризующее независимые выборки, корректируют на величину, учитывающую влияние корреляции между объединяемыми объектами:
, характеризующее независимые выборки, корректируют на величину, учитывающую влияние корреляции между объединяемыми объектами:
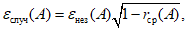 (5.17)
(5.17)
где
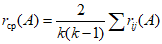 - среднее значение коэффициента корреляции между оценками параметра
A
по всем
k
водосборам. Найденное значение случайной составляющей используют для вычисления географической составляющей по
формуле (5.10)
;
- среднее значение коэффициента корреляции между оценками параметра
A
по всем
k
водосборам. Найденное значение случайной составляющей используют для вычисления географической составляющей по
формуле (5.10)
;
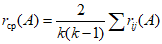 - среднее значение коэффициента корреляции между оценками параметра
A
по всем
k
водосборам. Найденное значение случайной составляющей используют для вычисления географической составляющей по
формуле (5.10)
;
- среднее значение коэффициента корреляции между оценками параметра
A
по всем
k
водосборам. Найденное значение случайной составляющей используют для вычисления географической составляющей по
формуле (5.10)
;
- если выполняется
условие (5.13)
, то по
формулам (5.14)
и
(5.15)
рассчитывают погрешность результата объединенного расчета, средневзвешенную по точности оценку и ее стандартную ошибку.
5.1.11 В случае неоднородности исходных данных гидрометрических наблюдений, обусловленной естественными факторами формирования стоковых характеристик или влиянием изменения климата, эмпирические и аналитические кривые распределения устанавливают отдельно для каждой однородной совокупности с применением составных кривых и (или) по сумме распределений на основе байесовских подходов.
5.1.11.1 Общую кривую распределения вероятностей превышения рассчитывают на основе составных кривых, установленных по однородным элементам одним из двух способов:
а) при наличии в каждом году наблюдений за всеми однородными элементами водного режима реки (
n
1
=
n
2
=
n
3
=
n
) ежегодную вероятность превышения
P
%
рассматриваемой гидрологической характеристики при любом ее значении определяют по формуле
где
P
1
,
P
2
,
P
3
- ежегодные вероятности превышения однородных элементов.
Для двух однородных гидрологических характеристик
формула (5.18)
принимает вид
б) если в каждом году имеется лишь одно значение элемента рассматриваемой гидрологической характеристики, ежегодные вероятности превышения при любом ее значении определяют по формуле
где
n
1
,
n
2
,
n
3
- число членов однородных элементов.
Для двух генетически однородных элементов
формула (5.20)
принимает вид
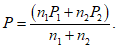 (5.21)
(5.21)
При наличии в ряду наблюдений нулевых значений рассматриваемой гидрологической характеристики (например, минимальные расходы воды) ежегодные вероятности превышения определяют по формуле
Вероятности превышения
P
1
,
P
2
,
P
3
в
формулах (5.18)
,
(5.19)
выражают в долях единицы, а в
формулах (5.20)
-
(5.22)
- в процентах. Параметры кривых распределения однородных элементов устанавливают согласно требованиям
5.1.5
-
5.1.9
.
5.1.11.2 Для расчета характеристик стока при наличии нарушений однородности
 рядов, обусловленных климатическими изменениями, временной ряд делится на несколько однородных частей, каждая из которых характеризуется своим набором параметров. Дата перехода характеристик стока из одного однородного состояния в другое определяется путем генетического и статистического анализа исходной гидрологической информации.
рядов, обусловленных климатическими изменениями, временной ряд делится на несколько однородных частей, каждая из которых характеризуется своим набором параметров. Дата перехода характеристик стока из одного однородного состояния в другое определяется путем генетического и статистического анализа исходной гидрологической информации.
 рядов, обусловленных климатическими изменениями, временной ряд делится на несколько однородных частей, каждая из которых характеризуется своим набором параметров. Дата перехода характеристик стока из одного однородного состояния в другое определяется путем генетического и статистического анализа исходной гидрологической информации.
рядов, обусловленных климатическими изменениями, временной ряд делится на несколько однородных частей, каждая из которых характеризуется своим набором параметров. Дата перехода характеристик стока из одного однородного состояния в другое определяется путем генетического и статистического анализа исходной гидрологической информации.
Определение расчетных характеристик речного стока на основе байесовских подходов в нестационарных условиях основано на построении закона распределения в виде суммы из нескольких законов распределения, взвешенных по продолжительности условно стационарных режимов. Расчетная кривая обеспеченности для всего ряда строится как сумма законов распределения с весами, пропорциональными длинам выборок.
Для определения расчетных значений для каждой из однородных частей ряда определяют кривую обеспеченности
P
i
(
x
). Составную кривую обеспеченности рассчитывают с использованием таблиц распределения Крицкого-Менкеля по формуле
Расчетная кривая обеспеченности строится подбором путем выполнения расчетов по
формуле (5.23)
для набора задаваемых значений расходов
x
.
Для расчетов речного стока в качестве математического вероятностного аппарата допускается использовать байесовскую методологию решения статистических задач для двух или трех условно стационарных периодов. В отличие от метода составных кривых обеспеченности, где в окончательном решении учитывают только весовые коэффициенты отдельных однородных совокупностей, при байесовском решении кроме длины однородных отрезков учитывают также погрешности выборочных оценок среднего значения.
При байесовском подходе для каждой из однородных частей ряда определяют
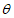 (параметр), в качестве которого могут рассматриваться: среднее значение, дисперсия и асимметрия, а также соотношения между ними. Параметр
(параметр), в качестве которого могут рассматриваться: среднее значение, дисперсия и асимметрия, а также соотношения между ними. Параметр
 является случайной величиной, поскольку его рассчитывают по ряду
y
(выборке) ограниченной длины. Распределение параметра
является случайной величиной, поскольку его рассчитывают по ряду
y
(выборке) ограниченной длины. Распределение параметра
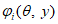 является выборочным и характеризуется параметрами, определяемыми по рекомендациям
5.1.9
,
5.1.10
.
является выборочным и характеризуется параметрами, определяемыми по рекомендациям
5.1.9
,
5.1.10
.
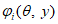 является выборочным и характеризуется параметрами, определяемыми по рекомендациям
5.1.9
,
5.1.10
.
является выборочным и характеризуется параметрами, определяемыми по рекомендациям
5.1.9
,
5.1.10
.
Вероятность, с которой процесс может находиться в одном из однородных состояний, принимается пропорциональной продолжительности соответствующего периода
 и
и
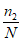 (в случае, если таких состояний два), где
N
=
n
1
+
n
2
- общая продолжительность неоднородной выборки наблюденных значений стока.
(в случае, если таких состояний два), где
N
=
n
1
+
n
2
- общая продолжительность неоднородной выборки наблюденных значений стока.
Распределение параметра
 является суммой двух выборочных распределений параметра для однородных частей выборки:
является суммой двух выборочных распределений параметра для однородных частей выборки:
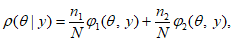 (5.24)
(5.24)
где
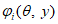 - выборочное распределение параметра
- выборочное распределение параметра
 для
i
-го наблюденного условно стационарного периода длиной
n
1
,
i
= 1, 2 с вероятностями
для
i
-го наблюденного условно стационарного периода длиной
n
1
,
i
= 1, 2 с вероятностями
 . Выборочное распределение параметра
. Выборочное распределение параметра
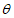 в большинстве случаев является нормальным распределением и задается двумя параметрами: среднее значение параметра и его среднее квадратическое отклонение.
в большинстве случаев является нормальным распределением и задается двумя параметрами: среднее значение параметра и его среднее квадратическое отклонение.
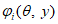 - выборочное распределение параметра
- выборочное распределение параметра
5.1.12 Для наибольшего и (или) наименьшего члена ряда наблюдений следует указывать доверительные интервалы для эмпирической ежегодной вероятности превышения
(таблица В.3)
.
5.1.13 Если точки эмпирической кривой распределения значительно отклоняются от аналитической кривой, рекомендуется на клетчатке вероятностей для этих точек также указывать доверительные границы и оценивать их однородность в соответствии с
таблицей В.3
.
При достаточной продолжительности рядов наблюдений рассчитывают случайные средние квадратические погрешности выборочных параметров и квантилей распределения.
Случайные средние квадратические погрешности выборочных средних определяют по приближенной зависимости:
- при нормальном исходном распределении ряда без учета автокорреляции между смежными членами ряда:
- при коэффициенте автокорреляции между смежными членами ряда
r
, меньшем 0,5, по формуле
- при коэффициентах автокорреляции >= 0,5 используют формулу
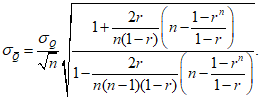 (5.27)
(5.27)
Случайные средние квадратические погрешности коэффициентов вариации при
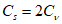 определяют по зависимости
определяют по зависимости
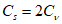 определяют по зависимости
определяют по зависимости
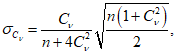 (5.28)
(5.28)
при отсутствии автокорреляции - по формуле
5.1.14 При наличии достоверных сведений о случайных относительных средних квадратических погрешностях исходных данных гидрометрических наблюдений оценки коэффициентов вариации и асимметрии уточняют по формулам:
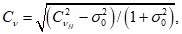 (5.30)
(5.30)
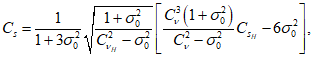 (5.31)
(5.31)
где
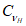 ,
,
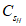 - коэффициенты вариации и асимметрии соответственно, рассчитанные по наблюденным значениям;
- коэффициенты вариации и асимметрии соответственно, рассчитанные по наблюденным значениям;
5.1.15 Параметры кривых распределения гидрологических характеристик при наличии обоснованных сведений о выдающихся значениях речного стока определяют следующим образом.
5.1.15.1 При учете одного выдающегося значения гидрологической характеристики, не входящего в непрерывный
n
-летний ряд данных гидрометрических наблюдений:
а) методом приближенного наибольшего правдоподобия в зависимости от статистик
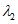 и
и
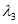 , определяемых по формулам:
, определяемых по формулам:
 (5.33)
(5.33)
б) методом моментов - по формулам:
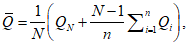 (5.34)
(5.34)
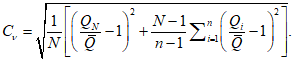 (5.35)
(5.35)
5.1.15.2 При учете одного выдающегося значения гидрологической характеристики, входящего в
n
-летний ряд данных гидрометрических наблюдений:
а) методом приближенного наибольшего правдоподобия в зависимости от статистик
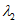 и
и
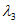 , определяемых по формулам:
, определяемых по формулам:
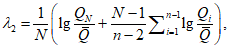 (5.36)
(5.36)
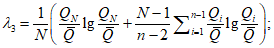 (5.37)
(5.37)
б) методом моментов - по формулам:
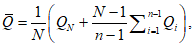 (5.38)
(5.38)
В
формулах (5.32)
-
(5.39)
:
n
- число лет наблюдений;
N
- число лет, в течение которых выдающееся значение гидрологической характеристики не было превышено.
Использование
формул (5.32)
-
(5.39)
допускается в случае, если исторические сведения о выдающемся гидрологическом значении и числе лет его непревышения обоснованы. Произвольное задание
Q
N
и
N
не допускается.
5.1.16 Боковую приточность между смежными створами определяют одним из следующих способов:
- суммированием расходов воды притоков с учетом времени добегания, впадающих на участке между двумя створами;
- по разности средних расходов воды в нижнем и верхнем створах участка реки;
- методом руслового водного баланса;
- по модулю стока, определенному по карте для частной площади.
Обработку рядов боковой приточности осуществляют в соответствии с настоящим разделом.
5.2 Годовой сток воды и его внутригодовое распределение
5.2.1 При определении расчетных гидрологических характеристик годового стока воды рек и его внутригодового распределения необходимо выполнять требования, изложенные в
4.3
-
4.11
и
5.1
.
5.2.2 Определение расчетного календарного внутригодового распределения стока при длительности рядов наблюдений проводят следующими методами:
- реального года;
- компоновки сезонов;
- среднего распределения стока за годы характерной градации водности.
5.2.3 Расчеты внутригодового распределения стока рек проводят по водохозяйственным годам (ВГ), начинающимся с первого месяца многоводного сезона. В отдельных случаях допускается выполнение расчетов внутригодового распределения стока для гидрологических лет, начинающихся с первого месяца периода накопления влаги, или для обычных календарных лет.
В зависимости от типа водного режима реки и преобладающего вида использования стока реки водохозяйственный год делят на два различающихся по длительности периода: лимитирующий (ЛП) и нелимитирующий (НП), а лимитирующий период соответственно на два сезона: лимитирующий (ЛС) и нелимитирующий (НС). Границы сезонов назначают едиными для всех лет с округлением до месяца.
5.2.4 Расчетное внутригодовое распределение месячного (а в отдельных случаях и декадного) стока определяют для водохозяйственного года расчетной вероятности превышения
P
расч
, соответствующей заданной проектной обеспеченности гарантированной отдачи. Длительность
n
многолетнего периода, необходимая для определения расчетного календарного внутригодового распределения стока, должна удовлетворять требованиям
5.1.1
. В зависимости от достаточной длительности наблюдений
n
, определенной по указанному критерию точности, выделяют следующие группы лет: по градациям вероятностей превышения стока реки за водохозяйственный год, а в методах компоновки и реального года также и за отдельные расчетные сезоны.
При периоде наблюдений
n
от 15 до 30 лет выделяют три группы лет: многоводные годы (
P
< 33,3%), средние по водности годы (33,3% <=
P
<= 66,7%) и маловодные годы (
P
> 66,7%). При продолжительности наблюдений более 30 лет выделяют пять групп: очень многоводные годы (< 16,7%), многоводные годы (16,7% <=
P
< 33,3%), средние по водности годы (33,3% <=
P
<= 66,7%), маловодные годы (66,7% <
P
<= 83,3%) и очень маловодные годы (
P
> 83,3%).
Во всех методах расчета по значениям стока за отдельные водохозяйственные годы (а в методах компоновки и реального года и за расчетные внутригодовые интервалы времени: лимитирующий период, лимитирующий сезон, нелимитирующий сезон, лимитирующий месяц) определяют расчетные квантили. Стандартными квантилями кривых распределения вероятностей стока являются следующие:
- для многоводных лет, периодов, сезонов и месяцев - 1%, 3%, 5%, 10% и 25%;
- для маловодных лет, периодов, сезонов и месяцев - 75%, 90%, 95%, 97% и 99%;
- для средних по водности лет - 50%.
При расчетах внутригодового стока по отдельным годам характерной водности для каждой обеспеченности из многолетнего ряда выбирают (или моделируют) наиболее неблагоприятный вариант внутригодового распределения для определенного вида водохозяйственной деятельности.
5.2.5 Определение внутригодового распределения стока методом реального года основано на выборе расчетного водохозяйственного года из числа фактических с использованием принципа наибольшей близости вероятностей превышения стока за водохозяйственный год, лимитирующий период, лимитирующий сезон и лимитирующий месяц к расчетной вероятности превышения и соответствует заданной по условиям проектирования вероятности превышения. Этот выбор осуществляют из числа
j
-х лет (от
j
= 1 до
j
=
m
;
m
- число лет с годовым стоком заданной градации водности) расчетной группы водности с использованием условия
где
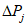 - суммарное отклонение, которое определяют для каждого из
m j
-х исследуемых водохозяйственных лет, вошедших в расчетную группу лет заданной градации водности;
- суммарное отклонение, которое определяют для каждого из
m j
-х исследуемых водохозяйственных лет, вошедших в расчетную группу лет заданной градации водности;
P
расч
- расчетная вероятность превышения, принимаемая одинаковой для всех расчетных интервалов времени;
P
ВГ
,
P
ЛП
,
P
ЛС
,
P
ЛМ
- значения вероятностей превышения стока за выбранный водохозяйственный год и его лимитирующий период, лимитирующий сезон и лимитирующий месяц в расчетном створе реки, определяемые по кривой вероятностей превышения соответствующего стокового ряда согласно
5.1
.
В качестве расчетного года принимают тот водохозяйственный год, для которого по
формуле (5.40)
получено наименьшее значение
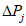 . Этот водохозяйственный год принимают в качестве модели относительного внутригодового распределения стока (в долях годового объема стока).
. Этот водохозяйственный год принимают в качестве модели относительного внутригодового распределения стока (в долях годового объема стока).
5.2.6 При использовании метода компоновки расчетные значения стока за водохозяйственный год, лимитирующий период, лимитирующий сезон и лимитирующий месяц определяют по соответствующим аналитическим кривым распределения стока с использованием принципа равенства расчетных вероятностей превышения стока
P
расч
за водохозяйственный год
P
ВГ
, лимитирующий период
P
ЛП
, лимитирующий сезон
P
ЛС
и лимитирующий месяц
P
ЛМ
. Сток за нелимитирующий период определяют по разности расчетных значений объемов стока за водохозяйственный год и лимитирующий период, сток за нелимитирующий сезон - по разности расчетных объемов стока за лимитирующий период и лимитирующий сезон, а суммарный объем стока всех нелимитирующих месяцев внутри нелимитирующего сезона - по разности расчетных объемов стока за лимитирующий сезон и лимитирующий месяц.
Расчетные значения месячного стока внутри лимитирующего сезона и нелимитирующего сезона определяют с таким расчетом, чтобы получить для этих сезонов наиболее неравномерные распределения стока.
С этой целью внутри каждого из этих сезонов, входящих в соответствующую группу водности, месячные объемы стока располагают в убывающем порядке с указанием календарных месяцев, к которым они относятся. Для составного периода (например, для лимитирующего периода), включающего в себя два сезона (лимитирующий сезон и нелимитирующий сезон), месячные объемы стока располагают в порядке убывания отдельно для каждого из составляющих их сезонов (лимитирующий сезон и нелимитирующий сезон). Каждому ранжированному месячному значению каждого из
m
лет, входящих в рассматриваемую группу водности, присваивают свой порядковый номер. Для всех
m
лет данной группы водности проводят суммирование месячных объемов стока, имеющих одинаковые порядковые номера в полученных ранжированных их внутрисезонных рядах. Путем сложения этих сумм для всех
k
месяцев, входящих в рассматриваемый сезон, находят их сумму за сезон. Делением сумм стока месяцев, имеющих одинаковые порядковые номера, на их общую сумму за сезон определяют относительное внутрисезонное распределение стока (по месяцам внутри сезона в долях от единицы или в процентах суммарного объема стока). Полученным средним месячным за
m
лет долям (или процентам) вместо присвоенных ранее порядковых номеров присваивают наименования того календарного месяца, который встречался наиболее часто при сложении указанных
m
значений месячного стока одинакового номера из всех лет рассматриваемой градации водности. Таким же или упрощенным способом (без ранжирования и перестановок месячных значений стока, то есть методом расчета средних месячных значений за годы данной градации водности) находят расчетные относительные месячные значения стока внутри нелимитирующего периода.
Расчетные месячные значения стока определяют как произведения их относительных значений (долей от сезонного) на расчетное значение стока соответствующего сезона заданной вероятности превышения. Эти расчеты проводят по однородным сезонам для всех месяцев ВГ. Относительное внутригодовое распределение месячного стока в долях (или процентах) от объема стока за водохозяйственный год вычисляют делением расчетных месячных объемов стока на расчетное годовое его значение заданной вероятности превышения.
5.2.7 Метод средних распределений стока за водохозяйственный год заданной градации водности основан на расчете средних относительных распределений месячных объемов стока от годовой их суммы путем осреднения относительных значений стока каждого
i
-го месяца за все годы, входящие в ту или иную градацию водности. Эти распределения являются типовыми для каждой отдельной группы характерных по водности лет. Расчетное распределение месячного стока вычисляют путем умножения месячных долей стока интересующей градации водности на объем стока за водохозяйственный год заданной вероятности превышения, определяемый по аналитической кривой обеспеченности.
Для районов, в которых расчетное распределение стока по сезонам и месяцам практически не зависит от водности года, расчеты рассматриваемым методом сводятся к установлению среднего по всем годам распределения стока по месяцам (декадам) в процентах от годового стока.
5.2.8 Определение расчетного внутригодового распределения суточного речного стока воды внутри года или характерного его периода, независимо от хронологического хода стока, проводят путем построения кривых продолжительности суточных расходов воды. Используют следующие виды кривых:
а) средняя многолетняя годовая кривая продолжительности суточных расходов воды, дающая характеристику среднего многолетнего типового распределения суточных расходов воды;
б) средняя многолетняя кривая продолжительности суточных расходов воды за тот или иной расчетный период года (навигационный, лесосплавный, вегетационный).
5.2.8.1 Выбор кривой определяется характером решаемой практической задачи. Кривые продолжительности суточных расходов воды строят следующим образом:
а) среднюю многолетнюю годовую кривую продолжительности суточных расходов воды определяют путем осреднения ординат ежегодных кривых среднесуточных расходов воды 30-, 90-, 180-, 270- и 355-суточной продолжительности (или соответствующих относительных продолжительностей стояния, равных 8%, 25%, 50%, 75% и 97% общей длительности года) и абсолютных (срочных) значений максимального и минимального расходов воды за конкретные годы наблюдений. Аналогичным образом строят среднюю многолетнюю кривую продолжительности стояния среднесуточных расходов воды за тот или иной расчетный внутригодовой период. Ее ординаты могут выражаться в долях среднемноголетнего расхода воды за рассматриваемый период (вегетационный, навигационный), а абсциссы - в долях его длительности;
б) ежегодную кривую продолжительности суточных расходов воды строят на основе расположенных в убывающем порядке суточных расходов воды конкретного года. Этим ранжированным значениям присваивают порядковые номера с 1-го по 365-й или 366-й. При этом в качестве расходов воды продолжительностью стояния 1 сут и 365 (или 366) сут используют данные соответственно о максимальном и минимальном срочном (а не среднесуточном) расходах воды.
Кривую продолжительности суточных расходов воды для расчетной части конкретного года строят аналогичным образом по данным о расположенных в убывающем порядке среднесуточных расходах воды и их порядковых номерах. Эти порядковые номера могут быть заменены их относительными характеристиками, выраженными в долях или в процентах общего числа в расчетном периоде. Выбор указанных расчетных внутригодовых периодов проводят с учетом целей проектирования и особенностей изучаемого объекта.
5.3 Максимальный сток воды весеннего половодья и дождевых паводков
5.3.1 Расчетные характеристики максимального стока воды рек весеннего половодья и дождевых паводков следует определять согласно требованиям
5.1
.
5.3.2 Для рек с продолжительностью стояния максимальных расходов воды весеннего половодья и дождевых паводков, равной суткам и более, расчет проводят по среднесуточным значениям, менее суток - по срочным расходам воды.
При прохождении максимального расхода воды между сроками наблюдений его значение определяют на основе установления соотношения между мгновенными и среднесуточными его значениями по данным измерений других лет с наибольшими расходами воды или по данным рек-аналогов.
5.3.3 При невозможности разделения максимальных годовых расходов воды на максимумы дождевых и талых вод допускается построение кривых распределения ежегодных вероятностей превышения максимальных расходов воды независимо от их происхождения.
5.3.4 При неоднородности максимальных расходов воды используют составные кривые распределения (см.
5.1.11
). Допускается также применение усеченных распределений, которые разработаны для частного случая, - разделение на две однородные совокупности по медианному значению. Сущность усечения кривой распределения состоит в том, что рассматривают только верхнюю часть кривой распределения максимальных расходов воды.
Основное расчетное выражение для оценки среднего значения
x
0
по методу приближенно наибольшего правдоподобия имеет следующий вид:
где
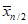 - среднее арифметическое значение верхней половины ранжированного ряда;
- среднее арифметическое значение верхней половины ранжированного ряда;
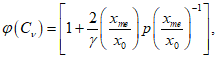 (5.43)
(5.43)
Оценку максимального правдоподобия коэффициента изменчивости
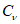 определяют через статистику
определяют через статистику
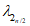 с помощью табулированной зависимости
(таблица Б.6)
, где
с помощью табулированной зависимости
(таблица Б.6)
, где
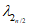 - статистика, вычисляемая по верхней половине ранжированного ряда (аналогично полному распределению):
- статистика, вычисляемая по верхней половине ранжированного ряда (аналогично полному распределению):
Порядок расчетов при использовании усеченного гамма-распределения следующий:
- исходный ряд располагается по убыванию;
- по
выражению (5.42)
находят среднее значение верхней половины ранжированного ряда
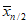 ;
;
- по
выражению (5.44)
вычисляют статистику
 ;
;
- по
выражению (5.41)
находят оценку
x
0
;
- отношение
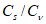 определяют в соответствии с
5.1.7
.
определяют в соответствии с
5.1.7
.
5.3.5 Расчетные максимальные расходы воды, объемы стока основной волны и всего половодья или паводка зарегулированных рек определяют для естественного состояния с учетом их изменений в результате хозяйственной деятельности в бассейне реки и трансформации проектируемыми или действующими водохранилищами.
На реках с каскадным расположением гидроузлов расчетные максимальные расходы воды, объемы стока, в том числе основных волн половодья или паводка, следует определять с учетом боковой приточности между гидроузлами и влияния вышележащих гидроузлов на приток к нижерасположенным.
5.3.6 К значениям расчетных максимальных расходов воды, объемов стока, в том числе основной волны, весеннего половодья (дождевого паводка), с вероятностью превышения 0,01% следует прибавлять гарантийную поправку для максимального расхода
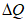 , для объемов стока (в том числе основной волны)
, для объемов стока (в том числе основной волны)
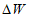 по соответствующим формулам:
по соответствующим формулам:
где
 - коэффициент, характеризующий гидрологическую изученность рек; принимают равным 1,0 для гидрологически изученных рек, когда выполняются условия
5.1.1
, во всех остальных случаях - 1,5;
- коэффициент, характеризующий гидрологическую изученность рек; принимают равным 1,0 для гидрологически изученных рек, когда выполняются условия
5.1.1
, во всех остальных случаях - 1,5;
N
- число лет наблюдений с учетом приведения к многолетнему периоду;
E
0,01%
- величина, характеризующая случайную среднюю квадратическую ошибку расчетного расхода воды или объема стока ежегодной вероятности превышения
P
= 0,01%, определяемая по
таблице В.4
.
Поправки
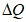 и
и
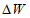 принимают равными не более чем 20% значения максимального расхода воды
Q
0,01%
и объема стока
W
0,01%
соответственно. Принимаемые расчетные расходы и объемы с учетом гарантийной поправки не должны быть меньше, чем наибольший наблюденный расход или объем.
принимают равными не более чем 20% значения максимального расхода воды
Q
0,01%
и объема стока
W
0,01%
соответственно. Принимаемые расчетные расходы и объемы с учетом гарантийной поправки не должны быть меньше, чем наибольший наблюденный расход или объем.
5.4 Расчетные гидрографы стока воды рек весеннего половодья и дождевых паводков
5.4.1 Расчетные гидрографы стока воды весеннего половодья и дождевых паводков необходимо рассчитывать при проектировании водохранилищ, отводе вод от сооружений в период их строительства, расчете затопления пойм и лиманов, пропуске высоких вод через дорожные и другие искусственные сооружения.
5.4.2 Форму расчетных гидрографов принимают по моделям наблюденных высоких весенних половодий или дождевых паводков с наиболее неблагоприятной их формой, для которых основные элементы гидрографов и их соотношения должны быть близки к расчетным.
Для расчета отверстий дорожных и других искусственных сооружений допускается принимать схематизацию гидрографов стока воды рек весеннего половодья и дождевых паводков по геометрическим формам.
5.4.3 Гидрографы речного стока следует рассчитывать по равнообеспеченным значениям максимального расхода воды, объема стока воды основной волны и объема всего весеннего половодья (дождевого паводка) расчетной вероятности превышения.
5.4.4 Расчетные гидрографы стока воды рек определяют:
а) по среднесуточным расходам воды, если максимальное значение расхода воды менее чем в 1,5 раза превышает соответствующий ему среднесуточный расход воды;
б) по мгновенным расходам воды, если максимальное значение расхода воды в 1,5 раза и более превышает соответствующий ему среднесуточный расход воды.
5.4.5 Выбор метода построения расчетного гидрографа и натурной модели зависит от задач, для решения которых он используется:
а) при проектировании гидротехнических объектов с относительно небольшой регулирующей емкостью водохранилища используют модель одновершинного гидрографа с наибольшим максимальным расходом воды;
б) при больших регулирующих емкостях, сопоставимых с полным объемом половодий (паводков), используют модель с наибольшим объемом половодья (паводка) и наибольшей сосредоточенностью стока в центральной части гидрографа;
в) для рек с многовершинными гидрографами следует выбирать такую модель из числа многоводных лет, в которой наибольшая волна после короткого промежутка следует за меньшей волной.
5.4.6 При каскаде водохранилищ принимают общую модель гидрографа для всего каскада. К нижележащим водохранилищам суммарный гидрограф рассчитывают с учетом трансформации половодья (паводка) вышележащими водохранилищами и боковой приточности.
В период прохождения половодного (паводочного) стока допускается применение имитационного моделирования гидрографов притока к отдельным участкам водохозяйственной системы, позволяющего учитывать асинхронность половодного (паводочного) стока, особенности его регулирования, время добегания на участках. Имитационное моделирование выполняют индивидуально с учетом особенностей функционирования каждого водохранилища каскада и требований к каскаду в целом.
5.4.7 Для развитых систем инженерной защиты, включающих наряду с водохранилищами обвалование, регулирование русла реки и другие мероприятия, строят расчетный гидрограф во входном створе на основной реке и гидрографы боковой приточности на всем протяжении инженерной защиты по общей для всей системы модели.
5.4.8 Основные элементы расчетного гидрографа стока воды рек: максимальный расход воды, объем весеннего половодья (дождевого паводка), объем основной волны расчетной вероятности превышения, а также боковую приточность определяют по данным гидрометрических наблюдений согласно требованиям
5.1
.
5.4.9 Общую продолжительность весеннего половодья для больших и средних рек, включая дождевые паводки на спаде половодья, принимают одинаковой для всех лет и створов как на основной реке, так и на притоках при условии включения в ее пределы продолжительности всех половодий (паводков).
Общую продолжительность весеннего половодья допускается принимать переменной для разных лет, но одинаковой по длине реки.
Продолжительность основной волны, включающей максимальную ординату, следует принимать постоянной в переменных календарных границах для всех лет исходя из условия наибольшего объема стока (притока) за принятый период.
а) переходом от гидрографа-модели к расчетному гидрографу путем умножения ординат гидрографа-модели на коэффициенты, определяемые по формулам:
k
2
= (
V
p
- 86400·
Q
p
)/(
V
m
- 86400·
Q
m
), (5.48)
 (5.49)
(5.49)
где
Q
m
,
Q
p
- максимальный среднесуточный расход воды весеннего половодья или мгновенный для дождевого паводка для гидрографа-модели и расчетного гидрографа соответственно, м
3
/с;
V
m
и
V
p
- объем основной волны для гидрографа-модели и расчетного гидрографа соответственно, м
3
;
б) переходом от гидрографа-модели к расчетному гидрографу с применением коэффициента
k
1
, определяемого по
формуле (5.47)
, и коэффициента
k
t
, определяемого по формуле
где
q
m
,
q
p
- модуль максимального среднесуточного расхода воды для гидрографа-модели и расчетного гидрографа соответственно, м
3
/(с·км
2
);
h
m
,
h
p
- слой стока весеннего половодья (дождевого паводка) для гидрографа-модели и расчетного гидрографа соответственно, мм.
Переход от гидрографа-модели к расчетному гидрографу по методу, указанному в
перечислении б)
, возможен только при соблюдении условий:
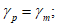
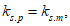
где
 ,
,
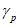 - коэффициент полноты для гидрографа-модели и расчетного гидрографа
- коэффициент полноты для гидрографа-модели и расчетного гидрографа
 соответственно, определяемый по формуле
соответственно, определяемый по формуле
 (5.51)
(5.51)
k
s
.
m
,
k
s
.
p
- коэффициент несимметричности для гидрографа-модели и расчетного гидрографа соответственно, определяемый по формуле
q
- модуль максимального среднего суточного расхода воды;
h
- слой стока весеннего половодья (дождевого паводка), мм;
t
- продолжительность весеннего половодья (дождевого стока), сут;
h
n
- слой стока за период подъема весеннего половодья (дождевого паводка), мм.
Координаты расчетного гидрографа определяют в зависимости от коэффициентов
k
i
и
k
t
по формулам:
Q
i
=
Q
i
,
m
k
i
, (5.53)
где
Q
i
,
m
,
Q
i
- расходы воды в
i
-ю единицу расчетного времени для гидрографа-модели и расчетного гидрографа соответственно, м
3
/с;
t
i
,
m
,
t
i
- ордината времени для гидрографа-модели и расчетного гидрографа соответственно.
За начало отсчета времени
t
i
,
m
принимают начало подъема весеннего половодья (дождевого паводка).
5.4.11 Определение гидрографов внутрисуточного хода стока следует проводить по методу, указанному в
5.4.10
. При этом принимают следующие обозначения в
формулах (5.50)
-
(5.54)
:
q
m
,
q
p
- модуль максимального мгновенного расхода воды для гидрографа-модели и расчетного гидрографа соответственно, м
3
/(с·км
2
);
h
m
,
h
p
- максимальный суточный слой стока весеннего половодья для гидрографа-модели и расчетного гидрографа соответственно, мм;
h
n
- слой стока за период подъема максимальной суточной волны весеннего половодья, мм;
t
- продолжительность максимальной суточной волны весеннего половодья, сутки и менее.
5.5.1 Определение расчетных минимальных расходов воды при наличии данных гидрологических наблюдений достаточной продолжительности проводят по кривым обеспеченности (см.
5.1.3
). При неоднородности ряда наблюдений применяют усеченные (см.
5.3.4
) или составные (см.
5.1.11
) кривые распределения ежегодных вероятностей превышения. Для расчетов используют минимальные среднесуточные, среднемесячные или 30-суточные (не календарные) расходы воды, наблюдавшиеся в зимний и (или) летне-осенний сезоны. В районах с частыми паводками могут быть расчетными минимальные средние расходы воды за 5 и 10 сут, в зависимости от решаемых задач.
5.5.2 При значительных расхождениях аналитической кривой и фактических данных в нижней части (резкое отклонение последних точек, обусловленное физическими причинами) применяют эмпирические кривые обеспеченности. Такие кривые имеют достаточно плавный вид в основной части и резкий изгиб в нижней. Обычно он приходится на зону обеспеченности в 90% - 97%.
5.5.3 При наличии нулевых расходов воды в ряду наблюдений расчеты проводят в соответствии с
5.1.11
, а в случае несоответствия полученной аналитической кривой наблюденным значениям - по эмпирической кривой вероятностей превышения.
5.6 Высшие уровни воды рек и озер
5.6.1 Расчетные высшие уровни воды рек в створе поста определяют по аналитической кривой распределения вероятностей превышения ежегодных высших мгновенных или срочных уровней воды за период многолетних наблюдений.
При значительных расхождениях аналитической кривой и фактических данных в верхней части (при наличии поймы) допускается использование эмпирических кривых обеспеченности.
Для рек, высшие уровни которых наблюдаются в разные фазы водного и ледового режимов, проводят обработку однородных рядов уровней, соответствующих снеговому половодью, дождевым паводкам и паводкам ледниковых вод при свободном состоянии русла, а также высших уровней при зажорах и заторах, осеннем и весеннем ледоходах. Вероятность превышения высших годовых уровней воды следует определять в соответствии с
5.1.2
.
При определении вероятности превышения высшего исторического уровня, установленного по данным опроса жителей или архивным источникам, принимают число лет, в течение которых он не был превышен.
Определение расчетных высших уровней воды озер следует проводить по кривым распределения вероятностей превышения уровней теми же приемами, что и для рек.
5.6.2 Расчетные уровни вверх или вниз по течению реки в случае свободного состояния русла переносят по одному из трех способов:
а) по кривым связи соответственных уровней воды;
б) по продольному профилю водной поверхности с учетом ее уклона при высоком уровне воды;
в) по кривым расходов воды
Q
=
f
(
H
).
Перенос уровней воды по продольному профилю водной поверхности проводят с учетом зависимости уклона от уровня, установленной в результате инженерно-гидрометеорологических изысканий в условиях установившегося движения потока.
Способ переноса расчетного высшего уровня воды по связи соответственных уровней между расчетным и опорным постами проводят по кривым связи ежегодных значений высших уровней воды или ежедневных значений уровней воды с учетом времени добегания воды между постами. Связь уровней считают удовлетворительной, если коэффициент корреляции
r
>= 0,8.
Данный способ может быть применен, если параллельными наблюдениями охвачено не менее 80% многолетней амплитуды колебания уровня воды в опорном створе и наличие надежной связи в верхней части кривой выявилось достаточно отчетливо.
В устьевых и приустьевых участках рек в отдельные фазы их режима следует учитывать возможность подпора воды со стороны водоприемника. Высшие уровни в пределах зон подпора переносят по кривой подпора.
Если высшие уровни приходятся на период с ледовыми явлениями, то их перенос осуществляют по графикам связи уровней или кривым
Q
=
f
(
H
) для открытого (свободного) русла и расходам воды, вычисленным по формуле
 (5.55)
(5.55)
где
Q
р%
- расход воды в опорном створе;
k
Q
- зимний коэффициент, учитывающий изменения гидравлических характеристик водного потока в результате ледовых явлений (ледохода, ледостава, скопления льда).
Если участок проектирования по условиям ледового режима однороден, то зимний коэффициент
k
Q
, характеризующий то или иное явление, принимают одинаковым для всех створов. При неоднородном ледовом режиме учитывают различие значений
k
Q
от створа к створу и значения этого коэффициента определяют в результате инженерно-гидрометеорологических изысканий.
Перенос высших уровней воды озер от опорного водомерного поста к другим постам проводят по графикам связи уровней воды или непосредственно по взаимно увязанным отметкам с учетом волнения и ветрового нагона.
Перенос уровней воды с помощью кривых
Q
=
f
(
H
) осуществляют на бесприточных и малоприточных участках рек, если для опорного створа имеется надежная кривая расходов воды и данные многолетних наблюдений за стоком.
5.6.3 Продолжительность стояния высших уровней устанавливают по хронологическим графикам уровней воды в период половодий и паводков, наиболее неблагоприятных по условиям затопления и подтопления застраиваемой территории. Вероятностные значения продолжительности стояния
T
р%
определяют по кривой обеспеченности ежегодной длительности превышения той или иной отметки затопления территории (например, отметки выхода воды на пойму). С учетом полученного значения
T
р%
строят расчетный график хода уровней по модели одного из наблюдавшихся продолжительных половодий или паводков. Пересчет ординат и абсцисс графика проводят с помощью переходных коэффициентов
K
H
и
K
T
.
K
H
= (
H
р%
-
H
Н.З
)/(
H
М
-
H
Н.З
) и
K
T
=
T
р%
/
T
М
, (5.56)
где
H
р%
и
T
р%
- высший расчетный уровень воды, см, и расчетная продолжительность стояния уровня, сут;
H
М
и
T
М
- высший уровень воды, см, и продолжительность для модельного графика колебания уровня воды, сут;
H
Н.З
- отметка начала затопления.
6 Определение расчетных гидрологических характеристик при недостаточности данных гидрометрических наблюдений
6.1.1 При недостаточности данных гидрометрических наблюдений параметры кривых распределения вероятностей гидрологических характеристик, а также основных элементов расчетного гидрографа необходимо приводить к многолетнему периоду с привлечением данных наблюдений пунктов-аналогов.
6.1.2 Приведение рассматриваемой гидрологической характеристики осуществляют в случаях, когда средняя квадратическая погрешность расчетного значения гидрологической характеристики превышает 10% для годового и сезонного стоков, 20% - для максимального и минимального стоков. Случайные средние квадратические погрешности определяют согласно
5.1.13
.
6.1.3 Основные требования при выборе пунктов-аналогов приведены в
4.9
. При выборе пункта-аналога основным критерием является наличие синхронности в колебаниях речного стока расчетного створа и створов-аналогов, которые количественно выражают через коэффициент парной или множественной (при одновременном использовании нескольких аналогов) корреляции между стоком в этих пунктах.
При выборе аналогов следует учитывать как возможно большую продолжительность наблюдений в этих пунктах, так и более тесные связи между стоком в приводимом к многолетнему периоду пункте и стоком в пунктах-аналогах.
При выборе пунктов-аналогов необходимо учитывать пространственную связанность рассматриваемой гидрологической характеристики, которую количественно выражают через матрицу парных коэффициентов корреляции или пространственную корреляционную функцию, представляющую собой зависимость коэффициентов парной корреляции стока рек от расстояния между центрами тяжести водосборов.
Матрицы парных коэффициентов корреляции и корреляционные функции определяют в однородном гидрологическом и физико-географическом районе.
6.1.4 При восстановлении значений стока за отдельные годы и расчете параметров и квантилей распределения необходимо проводить статистическую оценку значимости и устойчивости получаемых решений с определением случайных и систематических погрешностей в соответствии с
6.1.6
.
6.1.5 При приведении допускается использование гидрометрической информации, а также метеорологической информации, период наблюдений за которой превышает период наблюдений за рассматриваемой гидрологической характеристикой.
При привлечении метеорологической информации могут быть использованы региональные зависимости рассматриваемой гидрологической характеристики от факторов, ее определяющих.
6.1.6 При расчете параметров распределения и значений стока за отдельные годы
Q
i
с использованием аналитических методов, основанных на регрессионном анализе, должны соблюдаться следующие условия:
где
n
- число совместных лет наблюдений в приводимом пункте и пунктах-аналогах (
n
>= 6 при одном аналоге,
n
>= 10 при двух и более аналогах) или число пунктов-аналогов при восстановлении с привлечением кратковременных наблюдений (
n
>= 6);
R
- коэффициент парной или множественной корреляции между значениями стока исследуемой реки и значениями стока в пунктах-аналогах;
k
- коэффициент уравнения регрессии;
R
кр
- критическое значение коэффициента парной или множественной корреляции (обычно принимают
R
кр
>= 0,7);
A
кр
,
B
кр
- критические значения отношений
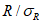 и
и
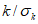 соответственно (обычно принимают
A
кр
>= 2,0 и
B
кр
>= 2,0).
соответственно (обычно принимают
A
кр
>= 2,0 и
B
кр
>= 2,0).
Если хотя бы один из коэффициентов уравнения регрессии не удовлетворяет
условию (6.1)
, то это уравнение не используют для приведения к многолетнему периоду.
6.2 Методы приведения рядов гидрологических характеристик и их параметров к многолетнему периоду с учетом материалов кратковременных (менее 6 лет) наблюдений
6.2.1 Методы учета материалов кратковременных наблюдений (инженерно-гидрометеорологических изысканий) предусматривают предварительное приведение к многолетнему периоду погодичных значений, параметров и квантилей распределения речного стока рек-аналогов исследуемого района согласно
6.3
при
n
>= 6.
6.2.2 Определение значений стока за каждый год, норм и квантилей распределения речного стока осуществляют по методу отношений, основанному на приблизительном равенстве модульных коэффициентов в пункте с кратковременными наблюдениями и в пунктах-аналогах, по формуле
где
Q
i
и
Q
ia
- наблюденные значения речного стока в пункте с кратковременными наблюдениями и в пунктах-аналогах с регулярными наблюдениями соответственно;
Q
и
Q
a
- в зависимости от требуемых решений могут обозначать восстанавливаемые значения стока за конкретные годы, погодичные значения за пределами гидрометрических наблюдений в пункте проектирования, норму стока или значения стока заданной обеспеченности.
6.2.3 Метод отношений используют при выполнении условия
R
>=
R
кр
, где
R
определяют по пространственной корреляционной функции. Пункты-аналоги с регулярными гидрометрическими наблюдениями при расчетах по методу, основанному на равенстве модульных коэффициентов, обычно выбирают по наименьшему расстоянию между центрами тяжести водосборов проектируемого пункта и пунктов-аналогов.
При наличии нескольких пунктов-аналогов расчеты осуществляют последовательно по всем аналогам и результаты осредняют (не более трех аналогов) с учетом случайных средних квадратических погрешностей в соответствии с
формулой (4.1)
.
6.2.4 Средняя квадратическая погрешность расчета значений стока за каждый год, нормы стока и квантилей распределения определяют по пунктам-аналогам. Для этой цели выбирают два пункта с гидрометрическими наблюдениями в однородном гидрологическом районе проектирования, один из которых условно принимают в качестве исследуемого пункта, а другой - в качестве пункта-аналога. Расчетное значение стока определяют по
формуле (6.2)
столько раз, сколько имеется наблюдений в створе, принимаемом за исследуемый.
Среднюю квадратическую погрешность погодичного значения или нормы стока, или квантилей распределения по данным одного года наблюдений определяют по формуле
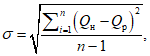 (6.3)
(6.3)
где
Q
н
- наблюденное значение стока за каждый год или норма стока, или квантили распределения;
Q
р
- рассчитанное значение стока за каждый год, или норма стока, или квантили распределения.
6.2.5 В соответствии с методикой восстановления значений стока по уравнениям регрессии, при наличии кратковременных наблюдений за один год, строят уравнения между всеми наблюдениями за этот год и последовательно за все остальные годы, для которых есть наблюдения в пунктах-аналогах, при условии, что количество пунктов должно быть не менее 5 - 6. Уравнения имеют следующий вид:
q
ij
=
B
1
i
q
kj
+
B
0
i
, (6.4)
где
q
ij
- значения стока в
j
-м пункте в
i
-й год за пределами кратковременных наблюдений;
q
kj
- значения стока в
j
-м пункте за
k
-й год, для которого есть данные кратковременных наблюдений;
B
1
i
,
B
0
i
- коэффициенты уравнений регрессий,
B
0
i
- свободный член.
6.2.6 В общем случае, если кратковременные наблюдения проводят в течение нескольких лет, строят зависимости для каждого года кратковременных наблюдений в соответствии с
6.2.5
. При этом результаты восстановления стока за каждый год, полученные по нескольким уравнениям, соответствующим числу лет кратковременных наблюдений, обобщают в соответствии с
формулой (4.1)
.
6.3 Методы приведения рядов гидрологических характеристик и их параметров к многолетнему периоду при наличии гидрометрических наблюдений 6 лет и более
6.3.1 Для расчета параметров распределения и значений гидрологических характеристик за отдельные годы используют аналитические методы, основанные на регрессионном анализе с привлечением одного или нескольких пунктов-аналогов на различных
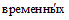 этапах при соблюдении
условий (6.1)
. Поэтапное использование нескольких аналогов расширяет возможности приведения и делает его более качественным по сравнению с методами, в которых используется дополнительная информация в одном пункте-аналоге.
этапах при соблюдении
условий (6.1)
. Поэтапное использование нескольких аналогов расширяет возможности приведения и делает его более качественным по сравнению с методами, в которых используется дополнительная информация в одном пункте-аналоге.
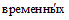 этапах при соблюдении
условий (6.1)
. Поэтапное использование нескольких аналогов расширяет возможности приведения и делает его более качественным по сравнению с методами, в которых используется дополнительная информация в одном пункте-аналоге.
этапах при соблюдении
условий (6.1)
. Поэтапное использование нескольких аналогов расширяет возможности приведения и делает его более качественным по сравнению с методами, в которых используется дополнительная информация в одном пункте-аналоге.
Уравнение множественной линейной регрессии, по которому восстанавливается сток, имеет общий вид
где
Q
- значение стока в приводимом пункте;
Q
j
...
Q
i
- значения стока в пунктах-аналогах;
k
0
- свободный член;
k
j
...
k
i
- коэффициенты уравнения регрессии при
j
= 1, 2, ...,
i
, где
i
- число пунктов-аналогов.
Коэффициенты и свободный член
уравнения (6.5)
определяют методом наименьших квадратов.
Одновременно используется не более двух-трех пунктов-аналогов.
6.3.2 В случае одного пункта-аналога приведение среднего значения к более длительному периоду осуществляют по формуле
где
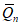 ,
,
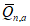 - среднеарифметические значения гидрологической характеристики для исследуемой реки и реки-аналога соответственно, вычисленные за период совместных наблюдений;
- среднеарифметические значения гидрологической характеристики для исследуемой реки и реки-аналога соответственно, вычисленные за период совместных наблюдений;
Относительную среднюю квадратическую погрешность приведенной к многолетнему периоду нормы стока определяют по формуле
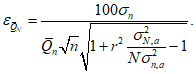 (6.7)
(6.7)
Коэффициент вариации
 определяют по формуле
определяют по формуле
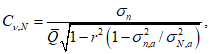 (6.8)
(6.8)
где
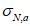 - среднее квадратическое отклонение гидрологической характеристики реки-аналога за
N
-летний период;
- среднее квадратическое отклонение гидрологической характеристики реки-аналога за
N
-летний период;
остальные обозначения - те же, что и в
формуле (6.6)
.
6.3.3 Данные, восстановленные по
уравнению (6.5)
, имеют систематически заниженную дисперсию. Исключение систематического уменьшения дисперсии восстановленных данных необходимо осуществлять одним из двух вариантов:
а) введением поправки в погодичные значения стока, полученные по уравнению регрессии
где
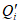 - погодичные значения гидрологических характеристик, рассчитанные по уравнению регрессии;
- погодичные значения гидрологических характеристик, рассчитанные по уравнению регрессии;
R
- коэффициент парной или множественной корреляции;
б) с учетом случайной составляющей отклонений наблюденных данных от рассчитанных по уравнению регрессии
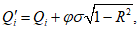 (6.10)
(6.10)
где
 - случайная величина, имеющая нормальный закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице; определяют по вероятности
P
, которую, в свою очередь, находят с помощью таблицы равномерно распределенных случайных чисел;
- случайная величина, имеющая нормальный закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице; определяют по вероятности
P
, которую, в свою очередь, находят с помощью таблицы равномерно распределенных случайных чисел;
Использование этого варианта рекомендуется осуществлять, если число восстановленных значений не менее 30.
Расчет параметров распределения осуществляют по ряду восстановленных значений без
поправки (6.9)
, и он не требует знания параметров ряда-аналога за весь
N
-летний период наблюдений.
6.3.4 При восстановлении значений речного стока за отдельные годы по методам, указанным в
6.2.6
и
6.3.3
, их окончательные значения могут определяться с учетом средних квадратических погрешностей методов по
формуле (4.1)
.
6.3.5 По восстановленному ряду совместно с наблюденными данными рассчитывают параметры распределения: среднее многолетнее значение, коэффициенты вариации и асимметрии и коэффициент корреляции между стоком смежных лет.
6.3.6 Расчетные значения коэффициентов асимметрии
C
s
и автокорреляции
r
(1) принимают на основании группового анализа отношения
 и
r
(1) по рекам-аналогам в соответствии с
5.1.7
.
и
r
(1) по рекам-аналогам в соответствии с
5.1.7
.
6.3.7 При оценке случайных средних квадратических погрешностей расчетных параметров речного стока необходимо учитывать объем информации, эквивалентной наблюденным данным, который определяют для среднего многолетнего значения
 и среднего квадратического отклонения
и среднего квадратического отклонения
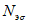 соответственно по формулам:
соответственно по формулам:
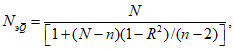 (6.11)
(6.11)
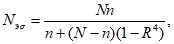 (6.12)
(6.12)
где
n
- число совместных лет наблюдений в приводимом ряду и рядах-аналогах;
N
-
n
- число восстановленных членов ряда по уравнению;
R
- коэффициент парной или множественной корреляции.
Так как зависимости между гидрологическими характеристиками не функциональны (
R
< 1), объем эквивалентно-независимой информации всегда больше
n
и меньше
N
, и только при
R
= 1
N
э
=
N
.
При поэтапном восстановлении значений ряда гидрологических характеристик, то есть при использовании нескольких уравнений регрессии за разные периоды, общий объем эквивалентно-независимой информации определяют как сумму этой информации за каждый восстановленный период.
6.4 Внутригодовое распределение стока
Ряды наблюденных значений стока за водохозяйственный год (ВГ), лимитирующий период (ЛП), лимитирующий сезон (ЛС), лимитирующий месяц (ЛМ) и другие месяцы года при недостаточной их длительности приводят к многолетнему периоду методами, изложенными в
6.1
-
6.3
. Исходные и приведенные к многолетнему периоду ряды следует проверять на однородность. Внутригодовые календарные распределения месячного (или декадного) стока в расчетном створе исследуемой реки или реки-аналога определяют методами, изложенными в
5.2.4
-
5.2.7
.
6.5 Расчетные гидрографы стока воды рек весеннего половодья и дождевых паводков
6.5.1 Для построения расчетных гидрографов боковой приточности должны быть использованы имеющиеся материалы гидрометрических наблюдений по притокам на участках рек или водохранилищ. Если эти материалы освещают режим только наиболее крупных притоков, то сток с остальной части бассейна следует определять по аналогии с гидрологически сходными изученными водосборами.
В зависимости от размеров водохранилища, расположения притоков по его длине и их водности расчетные гидрографы боковой приточности можно строить для всего водохранилища в целом или для его отдельных участков.
6.5.2 Форму модели расчетного гидрографа стока воды при условии выполнения требований
5.4.2
принимают согласно
5.4.9
,
5.4.10
.
6.5.3 Модель расчетного гидрографа стока воды устанавливают путем осреднения нескольких гидрографов стока воды высоких весенних половодий (дождевых паводков), выраженных в относительных единицах. Координаты натурных гидрографов
 и
Q'
из абсолютных значений пересчитывают в относительные (
t
i
,
Q
i
) в долях общей продолжительности паводка
t
m
и максимального расхода
Q
m
:
и
Q'
из абсолютных значений пересчитывают в относительные (
t
i
,
Q
i
) в долях общей продолжительности паводка
t
m
и максимального расхода
Q
m
:
 (6.13)
(6.13)
 (6.14)
(6.14)
Ординаты совмещают на одном чертеже относительно модальной ординаты. Затем по осредненным значениям ординат строят обобщенный гидрограф, наиболее полно отражающий особенности формы натурных гидрографов. Этот гидрограф и принимают за модель.
6.6 Минимальный сток воды рек
В расчетах минимального стока при небольшом числе лет совместных наблюдений (до 6 лет) с рекой-аналогом для более надежного выявления связи в условиях меженных периодов рекомендуется использовать значения расходов воды за меженный период согласно требованиям
5.5
.
6.7 Высшие уровни воды рек и озер
6.7.1 Высшие уровни воды рек и озер при недостаточности данных гидрометрических наблюдений приводят к многолетнему периоду методами, изложенными в
6.1
-
6.3
.
6.7.2 На реках, где максимумы уровней однозначно связаны с расходами воды, экстраполяцию эмпирической кривой обеспеченности высших уровней за пределы наблюденных значений выполняют с помощью аналитических функций распределения вероятностей превышения расходов воды. Для этого непродолжительные ряды расходов воды приводят к многолетнему периоду в соответствии с
6.1
,
6.2.1
-
6.2.5
. От расчетного максимального расхода к соответствующему уровню переходят по кривой расходов, координаты верхней части которой рассчитывают по формуле Шези с выделением элементов расходов воды в русле и пойме.
Если под влиянием русловых и гидравлических факторов зависимость между расходами и уровнями воды неоднозначна, то расчетный уровень воды за пределами наблюденных значений определяют по кривой связи уровня и поперечного сечения водного потока через значения, полученные по аналитической функции распределения вероятностей превышения значений.
6.7.3 В случае неоднозначности кривой расходов, обусловленной переменным подпором, для приведения кривых распределения ежегодных вероятностей превышения высших уровней воды к многолетнему периоду используют отклонения уровня от стандартной (осредненной) кривой
Q
=
f
(
H
) или от нижней устойчивой кривой.
Если в течение длительного периода наблюдается одностороннее смещение кривой
Q
=
f
(
H
) вверх или вниз, то это свидетельствует о происходящем намыве или размыве русла в исследуемом створе или в створе переката, лимитирующего уровень поста. Для экстраполяции высших уровней воды до отметок заданной вероятности превышения изложенным способом на деформируемых участках рек используют отклонения уровня от кривой
 .
.
 .
.
Ряд заторных и зажорных максимумов уровня возможно удлинить, если представить их в виде суммы уровня, соответствующего в условиях свободного ото льда русла расходу воды в момент вскрытия (замерзания) реки, и превышения над ним, что позволяет учесть дополнительную информацию о случаях вскрытия (замерзания), когда скопление льда не формируется на расчетном участке реки. Интегральная кривая распределения вероятностей высших заторных (зажорных) уровней совпадает при этом в нижней своей части с кривой обеспеченности уровней вскрытия (замерзания). Точка соединения кривых соответствует повторяемости заторов (зажоров) льда.
Расчетные уровни воды озер редкой повторяемости за пределами наблюденных находят путем экстраполяции аналитической кривой обеспеченности объемов воды
V
в озере. Необходимые для этого координаты зависимости
V
=
f
(
H
) устанавливают в результате инженерно-гидрометеорологических изысканий.
7 Определение расчетных гидрологических характеристик при отсутствии данных гидрометрических наблюдений
7.1 Общие положения
7.1.1 При отсутствии данных гидрометрических наблюдений в расчетном створе применяют региональные методы расчета гидрологических характеристик, основанные на результатах обобщения данных гидрометеорологических наблюдений и результатах инженерно-гидрометеорологических изысканий в районе проектирования, в соответствии с
4.3
.
Оценку точности определения расчетных гидрологических характеристик осуществляют в соответствии с
4.11
и
5.1.14
. Среднюю квадратическую погрешность расчета по региональным зависимостям определяют с учетом отклонений эмпирических точек от этих зависимостей.
Наряду с предлагаемыми в настоящем разделе формулами допускается применять другие региональные формулы при их обосновании (см.
4.11
).
7.1.2 При отсутствии гидрометрических наблюдений в расчетном створе параметры распределения и расчетные значения определяют с помощью следующих основных методов:
- гидрологическая аналогия;
- осреднение в однородном районе;
- построение карт изолиний;
- построение региональных зависимостей стоковых характеристик от основных стокоформирующих факторов;
- водно-балансовый.
7.1.3 Общие условия по выбору рек-аналогов приведены в
4.9
. Для каждой гидрологической характеристики следует учитывать дополнительные условия, которые приведены в данном разделе. В качестве одного из основных требований является наличие достаточно продолжительного ряда на реке-аналоге (см.
5.1.1
), который при недостаточности наблюдений приводят к многолетнему периоду в соответствии с
разделом 6
.
7.1.4 При статистической однородности параметров распределения в гидрологическом районе расчетное значение параметров в исследуемом створе следует определять как среднеарифметическое значение для рек-аналогов, имеющих наиболее продолжительные ряды наблюдений. Однородность параметров распределения устанавливают по статистическим критериям однородности согласно
4.6
.
7.1.5 Значения гидрологических характеристик допускается определять по районным картам, которые строят на основе использования всей имеющейся к моменту проектирования гидрологической информации согласно
4.2
. Районные карты строят для параметров распределения, расчетных гидрологических характеристик, коэффициентов региональных зависимостей с общей для территории структурой. Наведение изолиний следует осуществлять с учетом случайных погрешностей исходных данных и случайных погрешностей, обусловленных ограниченностью принятых в расчет выборок. Построение карт изолиний рассматриваемой гидрологической характеристики или параметра осуществляют методами линейной интерполяции, оптимальной интерполяции, основанной на пространственной корреляционной функции, и др. При этом использование пространственной корреляционной функции включает оценку ее однородности. В случае определяющего влияния других региональных факторов (например, высоты водосборов в горных районах) интерполяцию осуществляют с учетом этих факторов.
7.1.6 Построение региональных зависимостей для параметров распределения и расчетных гидрологических характеристик включает следующие основные этапы:
- выбор предполагаемых основных физико-географических факторов для исследуемого однородного района (площадь водосбора, средняя высота, уклон водосбора и реки, озерность, заболоченность, залесенность, метеорологические факторы);
- построение и анализ однофакторных зависимостей гидрологических характеристик от региональных факторов в целях выбора основных факторов для исследуемого региона, априорной оценки вида зависимостей и необходимости функциональных преобразований рассматриваемых факторов;
- предварительное формирование общей структуры региональной зависимости на основе генетического анализа и условий формирования стока, результатов анализа однофакторных зависимостей;
- построение региональных зависимостей с учетом
условий (6.1)
и формирование окончательного вида расчетных формул;
- оценка эффективности построенных региональных зависимостей и формул в соответствии с
4.11
.
В связи с ограниченностью данных и преобладающим влиянием характеристик физико-географических факторов в однородном районе региональные зависимости включают несколько (не более 4 - 5) основных переменных. В приведенных в настоящем разделе пунктах, касающихся конкретных гидрологических характеристик (годовой, максимальный, минимальный стоки, наивысшие уровни воды), указаны наиболее распространенные структуры региональных зависимостей и формул, применяющихся в гидрологических расчетах. Параметры этих зависимостей для каждого однородного региона следует определять на основе всей имеющейся информации, а оценку эффективности получаемых параметров и рассчитываемых по этой зависимости значений осуществляют в соответствии с
формулой (4.1)
и
4.11
.
7.1.7 Основными гидрографическими и физико-географическими факторами для построения региональных зависимостей являются следующие:
а) площадь водосбора
A
, км
2
;
б) гидрографическая длина водотока
L
, км;
в) средневзвешенный уклон водотока
I
,
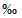 , представляющий собой условный выровненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов профиля водотока, вычисляемый по формуле
, представляющий собой условный выровненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов профиля водотока, вычисляемый по формуле
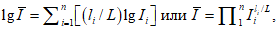 (7.1)
(7.1)
где
I
i
- частный средний уклон отдельных участков продольного профиля водотока;
l
i
- длина частных участков продольного профиля между точками перегиба, км;
L
- гидрографическая длина водотока до пункта наблюдений, км.
Средневзвешенный уклон определяют только для незарегулированных водотоков, а также для участков рек, расположенных в нижних бьефах водохранилищ;
г) средняя высота водосбора
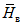 , м, над уровнем моря; определяют по гипсографической кривой водосбора или по формуле
, м, над уровнем моря; определяют по гипсографической кривой водосбора или по формуле
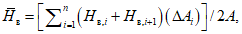 (7.2)
(7.2)
где
H
в,
i
- высота поверхности горизонтального сечения (горизонтали), м;
A
- общая площадь водосбора, км
2
;
д) относительная лесистость водосбора
f
л
, %, общей площади водосбора (лес и кустарники на проходимых болотах в лесные угодья не включают);
е) относительная заболоченность водосбора
f
б
, %, общей площади водосбора; вычисляют с разделением болот на верховые и низинные;
ж) относительная озерность водосбора
f
оз
, %, представляющая собой отношение суммы площадей всех озер, расположенных на водосборе, к общей площади водосбора;
и) средневзвешенная озерность для непроточных озер
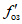 , %, общей площади водосбора; вычисляют с учетом расположения озер на водосборе по формуле
, %, общей площади водосбора; вычисляют с учетом расположения озер на водосборе по формуле
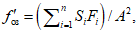 (7.3)
(7.3)
где
S
i
- площадь зеркала озер;
F
i
- площадь водосбора реки, замыкаемая озерами;
A
- площадь водосбора реки до замыкающего створа;
к) закарстованность водосбора
f
к
, %, общей площади водосбора; определяют отношением закарстованной площади водосбора ко всей его площади;
л) относительная распаханность водосбора
f
р
, %, общей площади водосбора; определяют отношением площади распаханных земель под сельскохозяйственные культуры на водосборе ко всей его площади;
м) относительные водонепроницаемые поверхности, %; определяют по крупномасштабным картам, топографическим планам, генеральным планам поселений и материалам аэрокосмических съемок;
н) характеристика типа почвогрунтов, слагающих поверхность водосбора; определяют по почвенным картам, а также выделяют пять групп почвогрунтов по механическому составу: глинистые, суглинистые, песчаные, супесчаные и каменистые;
п) средняя глубина залегания уровня грунтовых вод (первого водоносного горизонта); определяют по гидрогеологическим картам;
р) характеристики зарегулированности речной системы искусственными водоемами (количество, расположение и регулирующие емкости);
с) характеристика рельефа (равнинный - относительное колебание высот в пределах водосбора менее 200 м, горный - относительное колебание высот на водосборе более 200 м).
7.1.8 Для водотоков малых рек (
F
< 200 км
2
) дополнительно определяют следующие характеристики:
а) средний уклон склонов водосбора
I
ск
,
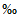 , определяют по картам и планам в горизонталях по формуле
, определяют по картам и планам в горизонталях по формуле
 (7.4)
(7.4)
где
h
- высота сечения рельефа, м;
б) густота речной сети водосбора
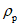 , км/км
2
; определяют как отношение суммарной длины всех водотоков (реки, каналы, канавы) на водосборе к общей площади водосбора:
, км/км
2
; определяют как отношение суммарной длины всех водотоков (реки, каналы, канавы) на водосборе к общей площади водосбора:
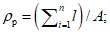 (7.5)
(7.5)
в) густота русловой сети водосбора
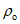 , км/км
2
; определяют как отношение суммарной длины речных долин, сухих русел, оврагов, балок и логов к общей площади водосбора.
, км/км
2
; определяют как отношение суммарной длины речных долин, сухих русел, оврагов, балок и логов к общей площади водосбора.
Гидрографические характеристики реки и ее водосбора определяют по топографическим картам, по цифровым картам соответствующего масштаба в зависимости от размера реки и рельефа водосбора по следующим рекомендациям:
1) для определения площадей водосборов, длин рек и уклонов - по
таблице 7.1
;
2) для определения гидрографических характеристик водоемов - по
таблице 7.2
;
г) характер почвогрунтов, степень закарстованности, глубина залегания уровня грунтовых вод; определяют по почвенно-грунтовым и гидрогеологическим картам.
Таблица 7.1
водосборов, длин рек и уклонов
|
Характер местности
|
Масштабы карт при площади водосбора, км
2
|
|||
|
< 10
|
10 - 50
|
50 - 200
|
> 200
|
|
|
Равнинные, пустынные и заболоченные слабо расчлененные районы
|
1:10000
|
1:25000
|
1:50000
|
1:100000
|
|
Горные и холмистые сильно расчлененные районы
|
1:25000
|
1:50000
|
1:100000
|
1:100000
|
Таблица 7.2
гидрографических характеристик водоемов
|
Водоемы
|
Площадь изображения водоема на карте, см
2
|
Масштабы карт
|
|
Крупнейшие и большие
|
> 1000
|
1:100000 - 1:500000
|
|
Средние
|
500 - 1000
|
1:50000 - 1:100000
|
|
Малые
|
100 - 500
|
1:25000 - 1:50000
|
|
Самые малые
|
10 - 100
|
1:10000 - 1:2500
|
Категории рек (большие, средние, малые) в зависимости от площади водосбора приняты в соответствии с
ГОСТ 19179
.
7.1.9 При определении гидрографических характеристик водотока и водосбора выбор масштаба топографических карт, установление местоположения водораздельных линий, истоков, устьев водотоков и картометрические измерения проводят в соответствии с
таблицами 7.1
и
7.2
.
7.1.10 Для восстановления многолетних рядов гидрологических характеристик при отсутствии данных гидрометрических наблюдений применяют зависимости стока от стокоформирующих факторов, которые строят для продолжительных рядов на реках-аналогах в однородном районе. Основная особенность при построении эмпирических зависимостей - их общая для территории структура, позволяющая интерполировать параметры, коэффициенты и стокоформирующие факторы на неизученный водосбор. Построение и анализ зависимостей осуществляют также в соответствии с требованиями
4.2
,
4.11
и
формулой (4.1)
.
7.2.1 При отсутствии наблюдений за стоком в расчетном створе параметры распределения (среднее, коэффициент вариации, отношение коэффициента асимметрии к коэффициенту вариации и коэффициент автокорреляции) определяют по рекам-аналогам.
7.2.2 В значения среднего многолетнего стока (нормы), определенные по районной карте, следует вводить поправки на влияние местных азональных факторов, которые учитывают неполное дренирование реками подземных вод, наличие карста, выходов подземных вод, особенности геологического строения бассейна, характер почв (грунтов), промерзание и пересыхание рек, различие средних высот водосборов и другие особенности. Поправки определяют путем построения зависимостей среднего многолетнего стока от азональных факторов.
7.2.3 Среднее многолетнее значение стока (в модулях или слоях стока) для расчетного пункта (центра тяжести водосбора) на равнинной территории или при незначительно меняющемся рельефе определяют линейной интерполяцией между изолиниями стока.
В случае пересечения водосбора несколькими изолиниями средневзвешенное значение стока вычисляют по формуле
q
ср
= (
q
1
A
1
+
q
2
A
2
+ ... +
q
n
A
n
)/
A
, (7.6)
где
q
1
, q
2
, ...,
q
n
- средние значения стока между соседними изолиниями, пересекающими водосбор;
A
1
,
A
2
, ...,
A
n
- соответствующие площади между изолиниями;
A
- общая площадь водосбора до расчетного створа.
7.2.4 Среднее многолетнее значение стока неисследованных горных рек следует определять по районным зависимостям стока от средней высоты водосбора, установленной для изученных рек в районе исследования.
В целях уточнения среднего многолетнего значения стока отдельных горных рек по зависимостям
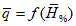 , составленным для достаточно крупных районов, используют дополнительные факторы (экспозицию склонов).
, составленным для достаточно крупных районов, используют дополнительные факторы (экспозицию склонов).
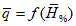 , составленным для достаточно крупных районов, используют дополнительные факторы (экспозицию склонов).
, составленным для достаточно крупных районов, используют дополнительные факторы (экспозицию склонов).
7.2.5 Значения коэффициента вариации
 неисследованных рек следует определять по карте изолиний этого параметра или по районным эмпирическим формулам, в которые вводят поправки на азональные факторы.
неисследованных рек следует определять по карте изолиний этого параметра или по районным эмпирическим формулам, в которые вводят поправки на азональные факторы.
Коэффициенты вариации по районным эмпирическим формулам определяют в зависимости от среднего многолетнего значения стока, площади водосбора реки или средней высоты бассейна (для горных районов).
На горных реках, в бассейнах которых имеются ледники, занимающие более 10% их общей площади, устанавливают районные зависимости коэффициента вариации от степени оледенения водосборов рек.
7.2.6 Коэффициент асимметрии устанавливают в соответствии с
5.1.7
.
7.2.7 При отсутствии рек-аналогов допускается построение региональных зависимостей годового стока от метеорологических факторов.
7.3 Внутригодовое распределение стока
7.3.1 При отсутствии данных гидрометрических наблюдений в створе проектирования расчетное внутригодовое распределение стока определяют по данным рек-аналогов, по районным схемам и по региональным зависимостям.
В первом случае относительные значения стока заданной вероятности превышения за все месяцы водохозяйственного года и соответствующей градации водности определяют путем расчета по данным достаточно длительных наблюдений на реке-аналоге, а во втором - путем составления районной схемы внутригодового распределения стока по результатам расчетов по группе рек-аналогов.
7.3.2 Применение метода аналогии для расчета внутригодового распределения стока рекомендуется для равнинных территорий и плоскогорий при сравнительно однообразных физико-географических условиях. Допускается при обосновании применение этого метода и для горных районов. За аналог принимают реку, удовлетворяющую условиям, приведенным в
4.9
.
7.3.3 Расчет внутригодового распределения стока проводят по региональным зависимостям параметров сезонного стока от определяющих факторов: площади водосбора реки, озерности, заболоченности, лесистости, характера почвогрунтов, а в горных условиях - также от средней высоты водосбора.
7.3.4 При приведении месячного, сезонного и годового стоков к многолетнему периоду используют рекомендации
раздела 6
. Определение расчетного внутригодового распределения стока по каждой из рек-аналогов проводят согласно рекомендациям
5.2.3
-
5.2.7
.
7.3.5 Основным методом обобщения данных по внутригодовому распределению стока, как для равнинных, так и для горных районов, является составление районных схем межсезонного и внутрисезонного распределений стока, необходимых для определения расчетного календарного распределения месячного стока в характерном по водности году исследуемой неизученной реки. Межсезонное распределение стока выражают в долях годового стока, а внутрисезонное распределение стока - в долях стока соответствующего сезона. В зависимости от характера решаемой практической задачи и принятого в расчетах метода определения внутригодового распределения стока для района исследования (или района проектирования) могут быть построены различные расчетные схемы. Общими при их установлении являются выявление и учет основных природных факторов (площади водосбора и озерности - на равнинах и плоскогорьях, средней высоты водосбора - в пересеченных горных районах).
7.3.6 Построение средней многолетней кривой продолжительности суточных расходов воды проводят методом аналогии. Среднюю многолетнюю кривую продолжительности, построенную для реки-аналога в относительных значениях (в долях ее среднемноголетнего годового расхода воды), переносят на неизученную реку с учетом нормы стока неизученной реки, полученной в соответствии с
7.2
.
7.4 Максимальный сток воды рек
7.4.1 Методы определения расчетных характеристик максимального стока весеннего половодья и дождевых паводков подразделяют на следующие:
а) при наличии одной или нескольких рек-аналогов;
б) при отсутствии рек-аналогов.
Значения параметров и коэффициентов в расчетных формулах следует уточнять на основе использования гидрометеорологической информации за весь период наблюдений, включая последние годы, в соответствии с
4.3
.
7.4.2 Выбор рек-аналогов следует проводить с соблюдением требований, указанных в
4.11
, а также при соблюдении условий:
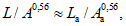 (7.7)
(7.7)
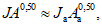 (7.8)
(7.8)
где
L
и
L
а
- длина исследуемой реки и реки-аналога соответственно, км;
J
и
J
а
- уклон водной поверхности исследуемой реки и реки-аналога соответственно,
 ;
;
A
и
A
а
- площади водосборов исследуемой реки и реки-аналога соответственно, км
2
.
7.4.3 При использовании нескольких независимых (но не более трех) региональных методов и схем расчета максимального стока окончательное расчетное значение рассматриваемой характеристики принимают в соответствии с
4.8
.
7.5 Весеннее половодье
7.5.1 При наличии рек-аналогов определение максимальных расходов воды весеннего половодья выполняют по редукционной
формуле (7.9)
.
7.5.2 Методы расчета максимальных расходов воды весеннего половодья применяют для рек с площадями водосборов от малых (менее 1 км
2
) до 20000 км
2
для европейской части России и до 50000 км
2
- для азиатской части, за исключением транзитных участков рек, где происходит сильное распластывание волны половодья, вызывающее снижение максимальных расходов воды.
При проектировании сооружений на реках с площадями водосборов, превышающими указанные пределы, максимальные расходы талых вод определяют по результатам инженерно-гидрометеорологических изысканий.
7.5.3 Расчетный максимальный расход воды весеннего половодья
Q
р%
, м
3
/с, заданной вероятности превышения
P
%
при наличии рек-аналогов определяют по редукционной формуле
где
K
0
- параметр, характеризующий дружность весеннего половодья; рассчитывают, как среднее из значений, определенных по данным нескольких рек-аналогов обратным путем из
формулы (7.9)
;
h
р%
- расчетный слой суммарного весеннего стока (без срезки грунтового питания), мм, ежегодной вероятности превышения
P
%
; определяют в зависимости от коэффициента вариации
 и отношения
и отношения
 , а также среднего многолетнего слоя стока
h
0
;
, а также среднего многолетнего слоя стока
h
0
;
A
- площадь водосбора исследуемой реки до расчетного створа, км
2
;
A
1
- дополнительная площадь, учитывающая снижение интенсивности редукции максимального модуля стока с уменьшением площади водосбора, км
2
;
n
- показатель степени редукции.
Показатель степени редукции
n
и параметр
A
1
в
формуле (7.9)
определяют на основе зависимости
q
max р%
=
f
(
A
) по данным наблюдений на изученных реках исследуемого района, где
q
max р%
- модуль максимального стока.
При обосновании в
формулу (7.9)
допускается введение дополнительных параметров, учитывающих влияние естественных и искусственных факторов на формирование максимального стока воды рек весеннего половодья.
7.5.4 Средний многолетний слой стока весеннего половодья
h
0
следует определять по данным рек-аналогов или интерполяцией по картам, построенным для исследуемого района с учетом последних лет наблюдений. В значение среднего многолетнего слоя весеннего стока вносят поправки на учет влияния местных факторов (площадь водосбора, уклоны склонов на водосборе, озерность, залесенность, заболоченность, распаханность, закарстованность):
а) для рек степной зоны Российской Федерации и полупустынной зоны Западной Сибири с площадями водосборов менее 3000 км
2
в значения
h
0
следует вводить поправки на учет площади водосбора на основе построения зависимости
h
0
=
f
(
A
) с учетом материалов наблюдений последних лет;
б) для малых равнинных рек с площадями водосборов менее 200 км
2
лесостепной, степной, полупустынной зон и засушливых степей поправочные коэффициенты устанавливают по зависимости
h
0
=
f
(
J
в
), где
J
в
- уклон водосбора;
в) при наличии озер, расположенных на водосборе реки, поправочные коэффициенты к среднему многолетнему слою стока весеннего половодья
h
0
определяют по связи слоя стока со значениями средней взвешенной озерности речных бассейнов
h
0
=
f
(
A
оз
), при этом параметр
A
оз
, %, определяют по формуле
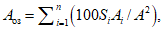 (7.10)
(7.10)
где
S
i
- площадь зеркала озера, км
2
;
A
i
- площадь водосбора озера, км
2
;
A
- площадь водосбора в расчетном створе реки;
г) для водосборов с залесенностью, отличной от средней зональной (районной), поправочный коэффициент определяют по соотношению
A
л
/
A
л.р
, где
A
л
- залесенность расчетного водосбора, %;
A
л.р
- среднее районное значение залесенности, %.
Вычисление среднего районного значения залесенности водосборов выполняют как среднеарифметическое из значений залесенности, %, по ближайшим речным водосборам (водосборы с
A
> 200 км
2
- для лесной и лесостепной зон и
A
> 2000 - 3000 км
2
для зон степей и полупустынь).
7.5.5 Коэффициент вариации слоя стока весеннего половодья принимают по рекам-аналогам или интерполяцией по картам изолиний этого параметра, построенным для исследуемого района.
Для рек с площадями водосборов
A
< 200 км
2
в значения, полученные интерполяцией по карте, следует вводить поправки, определяемые по зависимостям
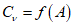 для равнинных рек и
для равнинных рек и
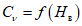 - для горных рек, где
H
в
- средняя высота речного бассейна, м.
- для горных рек, где
H
в
- средняя высота речного бассейна, м.
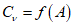 для равнинных рек и
для равнинных рек и
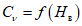 - для горных рек, где
H
в
- средняя высота речного бассейна, м.
- для горных рек, где
H
в
- средняя высота речного бассейна, м.
7.5.6 Расчетное значение отношения коэффициента асимметрии к коэффициенту вариации
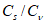 устанавливают в соответствии с требованиями
5.1.7
.
устанавливают в соответствии с требованиями
5.1.7
.
7.5.7 Коэффициент
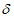 , учитывающий снижение максимального расхода воды весеннего половодья на реках, зарегулированных проточными озерами, следует определять по формуле
, учитывающий снижение максимального расхода воды весеннего половодья на реках, зарегулированных проточными озерами, следует определять по формуле
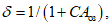 (7.11)
(7.11)
где
C
- коэффициент, принимаемый равным 0,2 для лесной и лесостепной зон и 0,4 - для степной зоны.
При наличии в бассейне озер, расположенных вне главного русла и основных притоков, значение коэффициента
 следует принимать:
следует принимать:
- для
A
оз
< 2% - 1;
- для
A
оз
> 2% - 0,8.
Влияние прудов, регулирующих меженный сток, при расчете максимальных расходов воды вероятностью превышения менее 5% не учитывают, а при
P
>= 5% допускается уменьшение расчетного значения обеспеченностью 10%.
7.5.8 Коэффициент
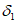 , учитывающий снижение максимальных расходов воды в залесенных бассейнах, определяют по формуле
, учитывающий снижение максимальных расходов воды в залесенных бассейнах, определяют по формуле
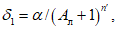 (7.12)
(7.12)
где
n'
- коэффициент редукции; устанавливают по зависимости
q
max
=
f
(
A
л
) с учетом преобладающих на водосборе почвогрунтов;
7.5.9 Коэффициент
 , учитывающий снижение максимальных расходов воды с заболоченных водосборов, определяют по формуле
, учитывающий снижение максимальных расходов воды с заболоченных водосборов, определяют по формуле
 (7.13)
(7.13)
где
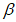 - коэффициент, определяемый в зависимости от типа болот и механического состава почвогрунтов вокруг болот и заболоченных земель (со слоем торфа не менее 30 см);
- коэффициент, определяемый в зависимости от типа болот и механического состава почвогрунтов вокруг болот и заболоченных земель (со слоем торфа не менее 30 см);
A
б
- относительная площадь болот, заболоченных лесов и лугов в бассейне реки, %.
Для горных рек коэффициенты
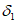 и
и
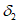 принимают равными единице.
принимают равными единице.
7.6.1 Расчетная формула для определения
Q
р%
для рек с площадями водосборов > 200 км
2
при наличии одной или нескольких рек-аналогов имеет вид
 (7.14)
(7.14)
где
q
р%,а
- модуль максимального срочного расхода воды реки-аналога расчетной вероятности превышения
P
%
, м
3
/(с·км
2
), рассчитывают по формуле
где
Q
р%,а
_
максимальный расход воды дождевого паводка вероятности превышения
P
%
, м
3
/с;
A
а
- площадь водосбора реки-аналога, км
2
;
здесь
L
и
L
а
- гидрографическая длина водотока для исследуемой реки и реки-аналога соответственно, км;
A
и
A
а
- площадь водосбора для исследуемой реки и реки-аналога соответственно, км
2
.
где Ф и Ф
а
- гидроморфометрическая характеристика русла для исследуемой реки и реки-аналога соответственно; определяют по формуле
здесь
L
и
A
- то же, что и в
формуле (7.16)
;
m
р
и
m
- гидравлические параметры, характеризующие состояние и шероховатость русла водотока; определяют согласно
таблице В.5
;
I
р
- средневзвешенный уклон русла водотока,
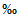 ;
;
n
и
n
1
- степенные коэффициенты, отражающие редукцию максимального модуля стока дождевого паводка
q
1%
с увеличением площади водосбора
A
, км
2
, и руслового времени добегания
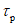 соответственно; определяются на основе анализа зависимостей
q
1%
=
f
(
A
) и
соответственно; определяются на основе анализа зависимостей
q
1%
=
f
(
A
) и
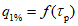 .
.
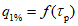 .
.
Русловое время добегания
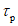 , мин, для гидрологически изученной реки определяют по формуле
, мин, для гидрологически изученной реки определяют по формуле
где
L
- то же, что и в
формуле (7.16)
;
V
- максимальное значение средней скорости добегания воды по главному водотоку, м/с;
m
р
,
m
и
I
р
- то же, что и в
формуле (7.19)
;
Коэффициент
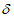 допускается определять по формуле
допускается определять по формуле
При наличии сведений только об относительной озерности
A
оз%
значение
C
о
для всех природных зон рекомендуется принимать равным 0,11; при наличии сведений о средневзвешенной озерности
 значение
C
о
рекомендуется принимать равным: 0,2 для лесной и лесостепной зон; 0,4 - для степной зоны.
значение
C
о
рекомендуется принимать равным: 0,2 для лесной и лесостепной зон; 0,4 - для степной зоны.
Коэффициент
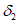 допускается определять по формуле
допускается определять по формуле
где
A
б
- относительная площадь болот и заболоченных земель на водосборе, %.
При необходимости в структуру расчетных формул следует вводить дополнительные параметры, учитывающие другие виды естественного и искусственного регулирования максимального дождевого стока рек, а также влияние изменения средней высоты водосбора для полугорных и горных районов. При этом следует сохранить основной принцип разработки структуры формул.
7.6.2 Расчетная формула для определения
Q
р%
при отсутствии рек-аналогов имеет вид
где
q
200
- модуль максимального срочного расхода воды ежегодной вероятности превышения
P
= 1%, приведенный к условной площади водосбора, равной 200 км
2
при
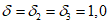 ; определяют для исследуемой реки при наличии региональной карты параметра
q
200
интерполяцией, а при отсутствии - на основе использования многолетних данных гидрологически изученных рек;
; определяют для исследуемой реки при наличии региональной карты параметра
q
200
интерполяцией, а при отсутствии - на основе использования многолетних данных гидрологически изученных рек;
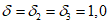 ; определяют для исследуемой реки при наличии региональной карты параметра
q
200
интерполяцией, а при отсутствии - на основе использования многолетних данных гидрологически изученных рек;
; определяют для исследуемой реки при наличии региональной карты параметра
q
200
интерполяцией, а при отсутствии - на основе использования многолетних данных гидрологически изученных рек;
A
- площадь водосбора, км
2
;
7.6.3 При отсутствии региональной карты параметр
q
200
в
формуле (7.23)
для исследуемой реки определяют интерполяцией по значениям этой характеристики, установленным для гидрологически изученных рек, а для рек полугорных и горных районов - на основе анализа графика связи
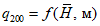 .
.
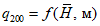 .
.
7.6.4 Расчетная формула для определения
Q
р%
на водосборах площадью менее 200 км
2
имеет вид
где
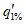 - относительный модуль максимального срочного расхода воды ежегодной вероятности превышения
P
= 1%, представляющий отношение
- относительный модуль максимального срочного расхода воды ежегодной вероятности превышения
P
= 1%, представляющий отношение
определяемый для исследуемого района в зависимости от гидроморфометрической характеристики русла Ф
р
и продолжительности склонового добегания
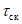 , мин;
, мин;
H
1%
- максимальный суточный слой осадков вероятности превышения
P
= 1%, мм; определяют по данным ближайших метеорологических станций;
Гидроморфометрическую характеристику русла исследуемой реки Ф
р
определяют по формуле
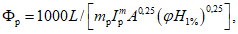 (7.27)
(7.27)
где
m
р
,
I
р
,
A
- то же, что и в
формуле (7.19)
.
7.6.5 При расчетах максимального стока по формуле предельной интенсивности редукционные кривые осадков уточняют при наличии данных наблюдений за последние годы.
7.6.6 При наличии реки-аналога порядок расчетов по
формуле (7.25)
следующий:
а) для исследуемого водотока устанавливают гидрографические характеристики, тип и механический состав почвогрунтов, слагающих водосбор, а также средний уклон склонов
I
ск
,
 , и густоту русловой и овражно-балочной сетей водосбора
, и густоту русловой и овражно-балочной сетей водосбора
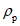 , км/км
2
;
, км/км
2
;
б) в соответствии с рекомендациями
4.9
и
7.4.2
выбирают реку-аналог (или несколько рек-аналогов), для которой (или которых) на основе статистической обработки многолетних рядов наблюдений за стоком воды определяют максимальный срочный расход воды дождевого паводка
Q
1%
вероятности превышения
P
= 1% в соответствии с требованиями
разделов 4
,
5
и по
формуле (7.15)
рассчитывают соответствующий максимальный срочный модуль стока
q
1%
и далее определяют значения расчетных максимальных срочных расходов воды дождевого паводка;
в) сборный коэффициент стока
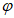 для равнинных рек определяют по формуле
для равнинных рек определяют по формуле
где
q
1%,а
- модуль максимального срочного расхода воды реки-аналога ежегодной вероятности превышения
P
= 1%, м
3
/(с·км
2
);
I
ск
,
I
ск,а
- средний уклон склона исследуемого водотока и реки-аналога соответственно;
n
2
- степенной коэффициент, определяемый в зависимости от механического состава почв и природной зоны;
n
3
- степенной коэффициент; принимают для лесотундры и лесной зоны равным 0,07, для остальных природных зон - 0,11;
здесь
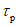 - продолжительность руслового добегания, мин; определяют по
формуле (7.20)
;
- продолжительность руслового добегания, мин; определяют по
формуле (7.20)
;
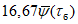 - ордината кривой редукции осадков. Расчетные значения суточных осадков определяют по кривым распределения ежегодных вероятностей превышения в соответствии с
5.1.3
;
- ордината кривой редукции осадков. Расчетные значения суточных осадков определяют по кривым распределения ежегодных вероятностей превышения в соответствии с
5.1.3
;
г) продолжительность склонового добегания
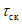 для водотоков, мин, допускается принимать в зависимости от природных зон равной следующим значениям:
для водотоков, мин, допускается принимать в зависимости от природных зон равной следующим значениям:
- тундра и лесная зона:
при заболоченности менее 20% .................................... 60;
при заболоченности от 20% - 40% ................................ 100;
при заболоченности более 40% ................................... 150;
- лесостепная зона ................................................ 60;
- степная зона и зона засушливых степей ........................... 30;
- полупустынная зона .............................................. 10;
- полугорные и горные районы ...................................... 10.
При наличии реки-аналога продолжительность склонового добегания
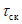 определяют в зависимости от района типовой кривой редукции осадков и гидроморфометрической характеристики склонов Ф
ск
, которую рассчитывают по формуле
определяют в зависимости от района типовой кривой редукции осадков и гидроморфометрической характеристики склонов Ф
ск
, которую рассчитывают по формуле
где
L
ск
- средняя длина безрусловых склонов водосбора; определяют по формуле
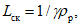 (7.31)
(7.31)
здесь
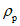 - густота русловой и овражно-балочной сети;
- густота русловой и овражно-балочной сети;
m
ск
- коэффициент, характеризующий шероховатость склонов водосбора; определяют по
таблице В.6
;
I
ск
- средний уклон склонов;
H
1%
- то же, что и в
формуле (7.25)
.
Значение
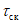 определяют методом последовательного приближения. По
формуле (7.29)
определяют бассейновое время добегания
определяют методом последовательного приближения. По
формуле (7.29)
определяют бассейновое время добегания
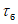 при значении
при значении
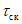 , принятом согласно
7.6.6
в зависимости от природных зон. Затем устанавливают значение
, принятом согласно
7.6.6
в зависимости от природных зон. Затем устанавливают значение
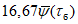 и по
формуле (7.28)
рассчитывают сборный коэффициент стока
и по
формуле (7.28)
рассчитывают сборный коэффициент стока
 . По
формуле (7.30)
определяют значение Ф
ск
и затем уточняют его в соответствии с
4.3
. При значительном расхождении полученного и первоначального значений
. По
формуле (7.30)
определяют значение Ф
ск
и затем уточняют его в соответствии с
4.3
. При значительном расхождении полученного и первоначального значений
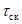 расчеты следует повторить, принимая за исходное последнее вычисленное значение
расчеты следует повторить, принимая за исходное последнее вычисленное значение
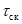 ;
;
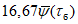 и по
формуле (7.28)
рассчитывают сборный коэффициент стока
и по
формуле (7.28)
рассчитывают сборный коэффициент стока
д) значение
H
1%
определяют по многолетним данным о максимальных суточных жидких осадках метеорологических станций, ближайших к бассейну исследуемого водотока, которые имеют наибольшую длительность наблюдений, или по региональной карте этой характеристики, построенной с учетом наблюдений последних лет;
е) максимальный срочный расход воды по
формуле (7.25)
при наличии рек-аналогов определяют с учетом значений параметров и характеристик этой формулы, полученных согласно рекомендациям
7.6.8
.
7.6.7 При отсутствии рек-аналогов расчет по
формуле (7.25)
проводят в последовательности, аналогичной приведенной в 7.15.6 при определении сборного коэффициента стока
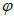 для равнинных рек, по формуле
для равнинных рек, по формуле
где
c
2
- эмпирический коэффициент, который для тундры и лесной зоны принимают равным 1,2; для остальных природных зон - 1,3;
n
2
,
n
3
,
A
- то же, что и в
7.6.6
.
Для водотоков со средним уклоном склонов более
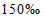 сборный коэффициент стока
сборный коэффициент стока
 рассчитывают по
формуле (7.32)
при
I
ск
, равном
рассчитывают по
формуле (7.32)
при
I
ск
, равном
 , а для водотоков со средним уклоном склонов менее
, а для водотоков со средним уклоном склонов менее
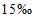 - при
I
ск
, равном
- при
I
ск
, равном
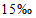 .
.
При различной крутизне склонов или значительной пестроте почвогрунтов, слагающих исследуемый водосбор, сборный коэффициент стока
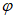 принимают как средневзвешенное значение.
принимают как средневзвешенное значение.
7.6.8 Расчетный слой дождевого паводка
h
р%
для водосборов площадью более 50 км
2
следует определять по формуле
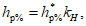 (7.33)
(7.33)
где
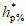 - слой дождевого паводка расчетной вероятности превышения
P
%
, мм; принимают по данным реки-аналога или по карте, построенной для гидрологически изученных рек, при
k
H
= 1;
- слой дождевого паводка расчетной вероятности превышения
P
%
, мм; принимают по данным реки-аналога или по карте, построенной для гидрологически изученных рек, при
k
H
= 1;
k
H
- эмпирический коэффициент, учитывающий уменьшение (редукцию) слоя дождевого паводка с увеличением площади водосбора в засушливых районах; устанавливают на основе исследования зависимости
h
р%
=
f
(
A
).
7.6.9 Расчетный слой дождевого паводка
h
р%
для водосборов площадью менее 50 км
2
при наличии рек-аналогов примерно такой же площади следует принимать равным расчетным слоям рек-аналогов.
При отсутствии рек-аналогов расчетные слои дождевого стока следует определять по формуле
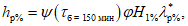 (7.34)
(7.34)
где
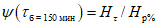 - относительная интенсивность осадков;
- относительная интенсивность осадков;
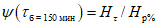 - относительная интенсивность осадков;
- относительная интенсивность осадков;
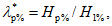 (7.35)
(7.35)
где
H
р%
и
H
1%
- слой максимальных суточных осадков вероятности превышения
P
%
и 1% соответственно, мм; определяют по кривым распределения суточных осадков;
7.7 Гидрографы стока воды рек весеннего половодья и дождевых паводков
7.7.1 Параметры основных элементов расчетного гидрографа следует определять согласно
5.4.1
-
5.4.10
,
7.5.3
-
7.5.9
,
7.6
.
7.7.2 Коэффициент перехода
k
t
от максимального мгновенного расхода воды весеннего половодья
 к среднесуточному
Q
р
устанавливают по рекам-аналогам. При их отсутствии для равнинных рек определение коэффициента
k
t
осуществляют по региональным зависимостям от площади водосбора.
к среднесуточному
Q
р
устанавливают по рекам-аналогам. При их отсутствии для равнинных рек определение коэффициента
k
t
осуществляют по региональным зависимостям от площади водосбора.
7.7.3 Одновершинный гидрограф стока воды весеннего половодья (дождевого паводка) рассчитывают согласно
таблице В.8
, по значению коэффициента несимметричности
k
s
, определяемого по
формуле (5.52)
, по данным рек-аналогов или по значению коэффициента формы гидрографа
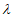 , определяемого по формуле
, определяемого по формуле
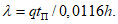 (7.36)
(7.36)
Ординаты расчетного гидрографа определяют по формуле
абсциссы - по формуле
t
i
=
xt
П
, (7.38)
где
t
П
- продолжительность подъема весеннего половодья (дождевого паводка), определяемая по формуле
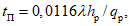 (7.39)
(7.39)
x
,
y
- относительные координаты расчетного гидрографа стока воды, определяемые по
таблице В.7
;
q
р
- расчетный модуль максимального среднего суточного расхода воды весеннего половодья или максимального мгновенного расхода воды дождевого паводка, м
3
/(с·км
2
).
7.7.4 Внутрисуточный гидрограф стока определяют по
формуле (7.37)
, значения относительных ординат
y
которого принимают по
таблице В.8
.
7.7.5 Для рек с площадью водосбора менее 200 км
2
с продолжительностью подъема дождевого паводка 1 сут или менее расчетную продолжительность определяют по формуле
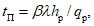 (7.40)
(7.40)
где
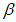 - коэффициент, принимаемый при расчете продолжительности подъема дождевого паводка в часах равным - 0,28; в минутах - 16,7.
- коэффициент, принимаемый при расчете продолжительности подъема дождевого паводка в часах равным - 0,28; в минутах - 16,7.
При определении расчетных гидрографов дождевых паводков согласно требованию
7.7.3
коэффициент несимметричности
k
s
следует принимать по рекам-аналогам; при отсутствии аналогов допускается
k
s
принимать равным 0,30; для рек с площадью менее 1 км
2
степной и полупустынной зон - 0,20.
7.8 Минимальный сток воды рек
7.8.1 Для равнинных и полугорных районов метод определения характеристик минимального расхода воды зависит от категории реки: малая, средняя или большая. К малым относят реки неполного дренирования подземных вод в их бассейнах, у которых модуль минимального стока увеличивается с возрастанием площади водосбора. К средним и большим относят реки с полным дренированием подземных вод на их водосборах.
7.8.2 Минимальные расходы воды на больших и средних реках определяют с использованием данных наблюдений на гидрологических постах, расположенных на этих реках, с учетом боковой проточности. При отсутствии данных наблюдений для средних рек применяют методы пространственной интерполяции минимального модуля стока 80%-ной обеспеченности.
7.8.3 Минимальный сток малых равнинных и полугорных рек
Q
р%
, м
3
/с, рассчитывают по зависимости минимальных расходов воды 80%-ной обеспеченности от площади водосбора, выявленной для районов, однородных по условиям формирования минимального стока. В общем виде эта зависимость имеет вид
где
b
,
m
- эмпирические коэффициенты, определяемые по рекам-аналогам на основе зависимости
Q
р%
=
f
(
A
-
A
1
);
A
- площадь водосбора, км
2
;
A
1
- площадь водосбора с ежегодным отсутствием стока в течение расчетного периода; определяется по рекам-аналогам;
Коэффициент
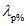 определяют как средний в однородном районе по данным рек-аналогов.
определяют как средний в однородном районе по данным рек-аналогов.
Зависимость (7.41)
используют для районов с относительной озерностью водосборов менее 2%, заболоченностью менее 5% и при отсутствии карста и многолетней мерзлоты.
Расчет минимального стока для неизученных малых рек с относительной озерностью более 2% и заболоченностью более 5% водосборов, а также расположенных в районах развития карста и многолетних мерзлых пород выполняется на основе результатов инженерно-гидрометеорологических изысканий в соответствии с
4.3
.
7.8.4 Минимальный среднесуточный расход воды расчетной обеспеченности определяют по формуле
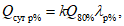 (7.42)
(7.42)
где
k
- коэффициент, определяемый как средний по району по связи суточных и средних минимальных расходов за принятый расчетный период (см.
5.5.1
).
7.8.5
Зависимость (7.41)
используют для районов с относительной озерностью водосборов менее 2%, заболоченностью менее 5% и при отсутствии карста и многолетней мерзлоты.
Расчет минимального стока для неизученных малых рек с относительной озерностью более 2% и заболоченностью более 5% водосборов, а также расположенных в районах развития карста и многолетних мерзлых пород выполняют на основе результатов инженерно-гидрометеорологических изысканий в соответствии с
4.3
.
7.9 Высшие уровни воды рек и озер
7.9.1 Расчетные высшие уровни воды, обусловленные половодьями и паводками, при свободном состоянии русла, определяют по кривым
Q
=
f
(
H
) через расходы воды
Q
р%
, рассчитанные способами, изложенными в
разделах 5
-
7
. При наличии поймы кривые расходов устанавливают отдельно для русла и поймы, а затем их суммируют.
Кривые расходов строят с помощью формулы
 (7.43)
(7.43)
где
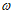 - площадь поперечного сечения русла или поймы, м
2
, при отметке уровня
H
;
- площадь поперечного сечения русла или поймы, м
2
, при отметке уровня
H
;
n
- коэффициент шероховатости, с/м
0,33
;
h
- средняя глубина воды в русле или пойме, м;
I
- уклон водной поверхности,
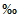 .
.
Зависимости
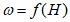 и
h
=
f
(
H
) устанавливают путем промеров глубин в реке и нивелирования русла и береговых склонов выше уреза воды до предполагаемой высоты уровня воды 1%-ной вероятности.
и
h
=
f
(
H
) устанавливают путем промеров глубин в реке и нивелирования русла и береговых склонов выше уреза воды до предполагаемой высоты уровня воды 1%-ной вероятности.
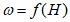 и
h
=
f
(
H
) устанавливают путем промеров глубин в реке и нивелирования русла и береговых склонов выше уреза воды до предполагаемой высоты уровня воды 1%-ной вероятности.
и
h
=
f
(
H
) устанавливают путем промеров глубин в реке и нивелирования русла и береговых склонов выше уреза воды до предполагаемой высоты уровня воды 1%-ной вероятности.
Определение гидравлических характеристик русла и поймы рек (уклонов водной поверхности, шероховатости русла и поймы) проводят в процессе инженерно-гидрометеорологических изысканий. Определение шероховатости выполняют с учетом
таблицы В.9
.
Расчет подпорных уровней на устьевых участках рек, а также в результате образования заторов и зажоров выполняют по результатам инженерно-гидрометеорологических изысканий согласно
4.3
.
7.9.2 Исходной характеристикой при расчете подпорных уровней на устьевых участках рек является наивысший уровень водотока или водоема водоприемника расчетной вероятности превышения, определяемый приемами, изложенными выше. Перенос этого уровня вверх от устья реки проводят по кривой подпора, которую строят путем соединения плавной вогнутой линией точек продольного профиля, соответствующих расчетному бытовому уровню воды в месте выклинивания подпора и в створе наибольшего подпора у его источника. Дальность распространения подпора
L
, км, определяют по формуле
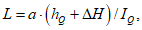 (7.44)
(7.44)
где
I
Q
и
h
Q
- средние уклон водной поверхности,
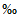 , и глубина реки, м, соответственно на расчетном участке при отсутствии подпора;
, и глубина реки, м, соответственно на расчетном участке при отсутствии подпора;
a
- коэффициент, зависящий от отношения
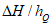 и определяемый по
таблице 7.3
.
и определяемый по
таблице 7.3
.
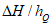 и определяемый по
таблице 7.3
.
и определяемый по
таблице 7.3
.
Таблица 7.3

|
5,0
|
2,0
|
1,0
|
0,5
|
0,3
|
0,2
|
0,1
|
0,05
|
|
a
|
0,96
|
0,91
|
0,85
|
0,76
|
0,67
|
0,58
|
0,41
|
0,24
|
7.9.3 Расчетные высшие уровни весеннего половодья рек устанавливают с учетом характера водного и ледового режимов реки. Расчетные высшие уровни воды рек в период ледохода определяют согласно требованиям
5.6.1
. Значения
k
зим
определяют по рекам-аналогам, а при их отсутствии принимают:
0,80 - 0,90 - для малых и средних рек;
0,91 - 0,95 - для больших рек.
7.9.4 Для определения высших уровней воды при заторах и зажорах льда требуется предварительно выполнить исследования в целях установления вероятности образования скоплений льда, их местоположения и мощности.
Возможность образования зажоров определяют следующие признаки:
- замерзание, происходящее путем перемещения кромки ледяного покрова снизу вверх по течению, что характерно для рек, которые текут с юга на север или выходят с гор на равнину;
- наличие в пределах участка проектирования или непосредственно ниже его перелома продольного профиля его водной поверхности с резким уменьшением к устью уклонов (в три раза и более), сужений русла, крутого поворота, островов и других русловых образований, уменьшающих льдопропускную способность русла;
- уклон водной поверхности выше очага зажорообразования, превышающий
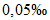 , при котором шуговые скопления вовлекаются под кромку ледяного покрова;
, при котором шуговые скопления вовлекаются под кромку ледяного покрова;
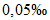 , при котором шуговые скопления вовлекаются под кромку ледяного покрова;
, при котором шуговые скопления вовлекаются под кромку ледяного покрова;
- интенсивный и длительный (6 сут и более) шугоход с расположенного выше по течению участка, что характерно для всех рек, процесс замерзания которых прерывается оттепелями, и для участков рек с большим тепловым стоком из глубоких озер и водохранилищ;
- большая осенняя водность [модуль стока более 3 л/(с·км
2
)].
7.9.5 При оценке возможности формирования заторов учитывают следующие факторы, способствующие заторообразованию:
- более позднее вскрытие участка реки, расположенного ниже по течению, которое характерно для рек, текущих с юга на север, при выходе рек с гор на равнину и в устьях рек;
- интенсивное снеготаяние и быстрый сброс воды в русловую сеть, чему благоприятствуют большой уклон и малые залесенность, заболоченность и озерность бассейна;
- наличие в пределах участка реки перелома продольного профиля водной поверхности с резким уменьшением уклона и русловых образований, уменьшающих льдопропускную способность русла;
- большие толщина и прочность льда перед вскрытием, наличие зажорных скоплений и наледей в пределах исследуемого участка, интенсивное поступление льда после вскрытия с расположенного выше по течению участка реки, а также с ранее вскрывающихся крупных притоков.
7.9.6 Расчетный наивысший уровень воды
H
з,р%
, обусловленный зажором или затором, вычисляют по формуле
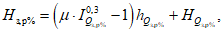 (7.45)
(7.45)
где
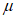 - коэффициент зажорности или заторности речного участка;
- коэффициент зажорности или заторности речного участка;
Q
з,р%
- расход воды в период зажоро- или заторообразования вероятности превышения
P
%
.
Коэффициент
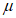 определяют путем полевых исследований, в ходе которых на временном гидрологическом посту ведут учащенные наблюдения за ледовыми явлениями и уровнем воды в период замерзания или вскрытия. Путем измерения скоростей перемещения льдин или расчета модулей стока оценивают расход
Q
з
и уровень
определяют путем полевых исследований, в ходе которых на временном гидрологическом посту ведут учащенные наблюдения за ледовыми явлениями и уровнем воды в период замерзания или вскрытия. Путем измерения скоростей перемещения льдин или расчета модулей стока оценивают расход
Q
з
и уровень
 воды. Последний может быть определен также с помощью графической срезки уровней с учетом данных о стоке воды. Уклон водной поверхности измеряют в период со свободным ото льда руслом.
воды. Последний может быть определен также с помощью графической срезки уровней с учетом данных о стоке воды. Уклон водной поверхности измеряют в период со свободным ото льда руслом.
При отсутствии полевых работ значение коэффициента зажорности (заторности)
 допускается принимать по
таблице 7.4
в зависимости от вида ледяного образования и приращения ширины реки, определяемого по формуле
допускается принимать по
таблице 7.4
в зависимости от вида ледяного образования и приращения ширины реки, определяемого по формуле
 (7.46)
(7.46)
где
 - ширина реки в расчетном створе, м, при уровне воды
- ширина реки в расчетном створе, м, при уровне воды
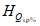 при свободном ото льда русле;
при свободном ото льда русле;
Таблица 7.4
|
Вид ледяного образования
|
Коэффициент
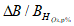
|
|||||
|
0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
|
|
Зажор
|
27,1
|
22,2
|
18,2
|
14,9
|
12,2
|
10
|
|
Затор
|
17,3
|
14,2
|
11,6
|
9,5
|
7,8
|
6,4
|
|
Зажор + затор
|
22,2
|
18,2
|
14,9
|
12,2
|
10,0
|
8,2
|
7.9.7 Расчетные значения высших уровней воды при подвижках льда и ледоходе оценивают по кривой
Q
=
f
(
H
) через расходы, вычисленные по формуле
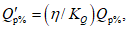 (7.47)
(7.47)
где
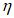 - коэффициент, учитывающий соотношение расходов воды при подвижке (ледоходе) и на пике весеннего половодья
Q
р%
и несовпадение по годам этих расходов одной вероятности превышения;
- коэффициент, учитывающий соотношение расходов воды при подвижке (ледоходе) и на пике весеннего половодья
Q
р%
и несовпадение по годам этих расходов одной вероятности превышения;
K
Q
- коэффициент, характеризующий изменение гидравлических характеристик водного потока льдом.
Значения коэффициентов
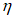 и
K
Q
определяют методом аналогии.
и
K
Q
определяют методом аналогии.
7.9.8 Для ориентировочных расчетов высших уровней воды проточных озер в зоне избыточного увлажнения используют зависимость
где
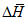 - средний многолетний весенне-летний подъем уровня воды в озере над порогом стока, см;
- средний многолетний весенне-летний подъем уровня воды в озере над порогом стока, см;
A
- площадь водосбора озера, км
2
;
Переход от среднего многолетнего подъема уровня к подъему расчетной вероятности превышения проводят по кривым обеспеченности с параметрами
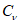 и отношением
и отношением
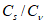 , установленным также по данным наблюдений на соседних, изученных морфологически однородных озерах.
, установленным также по данным наблюдений на соседних, изученных морфологически однородных озерах.
Зависимость (7.48)
применима для отношения
 менее 250.
менее 250.
В значения расчетных уровней вводят поправки на нагон
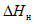 и ветровое волнение
и ветровое волнение
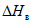 , которые рассчитывают по методикам, приведенным в
СП 38.13330
. При расчете
, которые рассчитывают по методикам, приведенным в
СП 38.13330
. При расчете
 учитывают расчетную скорость ветра, среднюю глубину водоема и расстояние пункта, для которого проводят расчет, от центра тяжести зеркала водоема. Поправку
учитывают расчетную скорость ветра, среднюю глубину водоема и расстояние пункта, для которого проводят расчет, от центра тяжести зеркала водоема. Поправку
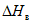 определяют с учетом ветровой защищенности исследуемой береговой зоны, длины разгона волны, расчетной скорости ветра и глубины водоема.
определяют с учетом ветровой защищенности исследуемой береговой зоны, длины разгона волны, расчетной скорости ветра и глубины водоема.
Для карстовых, периодически исчезающих озер, а также для озер с искаженным естественным режимом проведение полевых исследований обязательно.
7.9.9 Расчеты высших уровней воды озер необходимо уточнять также с учетом результатов инженерно-гидрологических изысканий согласно
4.3
.
ТАБЛИЦЫ СТАТИСТИК ОДНОРОДНОСТИ И СТАЦИОНАРНОСТИ
Таблица А.1
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,70
|
0,53
|
0,39
|
0,34
|
0,31
|
0,28
|
0,25
|
|
0,5
|
0,70
|
0,52
|
0,38
|
0,32
|
0,28
|
0,26
|
0,23
|
|
|
0,9
|
0,66
|
0,47
|
0,32
|
0,27
|
0,22
|
0,20
|
0,17
|
|
|
5
|
0
|
0,56
|
0,41
|
0,30
|
0,26
|
0,22
|
0,20
|
0,18
|
|
0,5
|
0,56
|
0,40
|
0,29
|
0,25
|
0,21
|
0,19
|
0,17
|
|
|
0,9
|
0,54
|
0,38
|
0,24
|
0,20
|
0,16
|
0,14
|
0,12
|
|
|
10
|
0
|
0,48
|
0,35
|
0,25
|
0,22
|
0,19
|
0,17
|
0,15
|
|
0,5
|
0,48
|
0,34
|
0,24
|
0,21
|
0,18
|
0,16
|
0,14
|
|
|
0,9
|
0,46
|
0,32
|
0,19
|
0,16
|
0,13
|
0,12
|
0,10
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,74
|
0,58
|
0,48
|
0,43
|
0,39
|
0,37
|
0,33
|
|
0,5
|
0,74
|
0,57
|
0,44
|
0,39
|
0,36
|
0,34
|
0,31
|
|
|
0,9
|
0,68
|
0,54
|
0,36
|
0,30
|
0,26
|
0,24
|
0,21
|
|
|
5
|
0
|
0,63
|
0,48
|
0,38
|
0,33
|
0,29
|
0,26
|
0,25
|
|
0,5
|
0,62
|
0,47
|
0,36
|
0,31
|
0,27
|
0,26
|
0,23
|
|
|
0,9
|
0,56
|
0,41
|
0,28
|
0,24
|
0,19
|
0,18
|
0,16
|
|
|
10
|
0
|
0,55
|
0,42
|
0,32
|
0,28
|
0,24
|
0,23
|
0,21
|
|
0,5
|
0,54
|
0,39
|
0,30
|
0,26
|
0,22
|
0,21
|
0,19
|
|
|
0,9
|
0,48
|
0,35
|
0,22
|
0,19
|
0,16
|
0,15
|
0,13
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,79
|
0,65
|
0,55
|
0,50
|
0,47
|
0,45
|
0,41
|
|
0,5
|
0,78
|
0,63
|
0,52
|
0,47
|
0,43
|
0,41
|
0,38
|
|
|
0,9
|
0,73
|
0,58
|
0,42
|
0,36
|
0,32
|
0,30
|
0,27
|
|
|
5
|
0
|
0,68
|
0,55
|
0,45
|
0,40
|
0,36
|
0,34
|
0,31
|
|
0,5
|
0,67
|
0,53
|
0,43
|
0,38
|
0,33
|
0,31
|
0,28
|
|
|
0,9
|
0,59
|
0,45
|
0,31
|
0,37
|
0,23
|
0,22
|
0,19
|
|
|
10
|
0
|
0,60
|
0,48
|
0,39
|
0,34
|
0,30
|
0,28
|
0,26
|
|
0,5
|
0,59
|
0,45
|
0,36
|
0,31
|
0,27
|
0,26
|
0,24
|
|
|
0,9
|
0,51
|
0,38
|
0,26
|
0,23
|
0,19
|
0,18
|
0,16
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,84
|
0,71
|
0,62
|
0,57
|
0,54
|
0,51
|
0,47
|
|
0,5
|
0,82
|
0,69
|
0,58
|
0,53
|
0,50
|
0,48
|
0,45
|
|
|
0,9
|
0,75
|
0,62
|
0,46
|
0,41
|
0,37
|
0,35
|
0,31
|
|
|
5
|
0
|
0,73
|
0,60
|
0,51
|
0,46
|
0,42
|
0,40
|
0,37
|
|
0,5
|
0,72
|
0,58
|
0,49
|
0,44
|
0,39
|
0,38
|
0,34
|
|
|
0,9
|
0,62
|
0,49
|
0,37
|
0,32
|
0,28
|
0,26
|
0,24
|
|
|
10
|
0
|
0,67
|
0,54
|
0,45
|
0,40
|
0,36
|
0,34
|
0,31
|
|
0,5
|
0,64
|
0,51
|
0,42
|
0,38
|
0,33
|
0,32
|
0,29
|
|
|
0,9
|
0,53
|
0,42
|
0,31
|
0,27
|
0,23
|
0,22
|
0,18
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,88
|
0,77
|
0,68
|
0,64
|
0,61
|
0,58
|
0,53
|
|
0,5
|
0,88
|
0,76
|
0,65
|
0,61
|
0,57
|
0,54
|
0,50
|
|
|
0,9
|
0,79
|
0,61
|
0,52
|
0,46
|
0,41
|
0,39
|
0,36
|
|
|
5
|
0
|
0,79
|
0,67
|
0,58
|
0,52
|
0,48
|
0,45
|
0,42
|
|
0,5
|
0,77
|
0,65
|
0,55
|
0,49
|
0,44
|
0,42
|
0,39
|
|
|
0,9
|
0,67
|
0,56
|
0,41
|
0,36
|
0,32
|
0,30
|
0,27
|
|
|
10
|
0
|
0,72
|
0,60
|
0,51
|
0,46
|
0,41
|
0,39
|
0,36
|
|
0,5
|
0,69
|
0,57
|
0,49
|
0,44
|
0,38
|
0,36
|
0,33
|
|
|
0,9
|
0,57
|
0,46
|
0,34
|
0,30
|
0,26
|
0,25
|
0,23
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,96
|
0,87
|
0,78
|
0,74
|
0,70
|
0,67
|
0,62
|
|
0,5
|
0,96
|
0,86
|
0,76
|
0,71
|
0,67
|
0,63
|
0,58
|
|
|
0,9
|
0,91
|
0,83
|
0,69
|
0,61
|
0,55
|
0,53
|
0,49
|
|
|
5
|
0
|
0,88
|
0,79
|
0,69
|
0,63
|
0,58
|
0,55
|
0,50
|
|
0,5
|
0,88
|
0,78
|
0,67
|
0,61
|
0,55
|
0,52
|
0,47
|
|
|
0,9
|
0,79
|
0,69
|
0,54
|
0,48
|
0,42
|
0,39
|
0,36
|
|
|
10
|
0
|
0,83
|
0,72
|
0,62
|
0,56
|
0,50
|
0,47
|
0,44
|
|
0,5
|
0,81
|
0,70
|
0,60
|
0,54
|
0,48
|
0,45
|
0,42
|
|
|
0,9
|
0,69
|
0,59
|
0,46
|
0,40
|
0,35
|
0,33
|
0,30
|
|
Таблица А.2
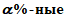 критические значения статистики Диксона (
D
1
I
)
критические значения статистики Диксона (
D
1
I
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,70
|
0,53
|
0,39
|
0,34
|
0,28
|
0,24
|
0,21
|
|
0,5
|
0,69
|
0,51
|
0,38
|
0,29
|
0,26
|
0,22
|
0,19
|
|
|
0,9
|
0,69
|
0,49
|
0,35
|
0,25
|
0,20
|
0,19
|
0,17
|
|
|
5
|
0
|
0,56
|
0,41
|
0,30
|
0,26
|
0,21
|
0,19
|
0,16
|
|
0,5
|
0,56
|
0,40
|
0,29
|
0,25
|
0,20
|
0,17
|
0,15
|
|
|
0,9
|
0,56
|
0,36
|
0,24
|
0,19
|
0,15
|
0,13
|
0,12
|
|
|
10
|
0
|
0,48
|
0,35
|
0,25
|
0,21
|
0,17
|
0,15
|
0,13
|
|
0,5
|
0,48
|
0,34
|
0,24
|
0,18
|
0,16
|
0,14
|
0,12
|
|
|
0,9
|
0,47
|
0,30
|
0,20
|
0,15
|
0,12
|
0,11
|
0,09
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,65
|
0,45
|
0,31
|
0,25
|
0,19
|
0,16
|
0,14
|
|
0,5
|
0,65
|
0,45
|
0,31
|
0,25
|
0,19
|
0,16
|
0,14
|
|
|
0,9
|
0,65
|
0,45
|
0,29
|
0,22
|
0,16
|
0,15
|
0,13
|
|
|
5
|
0
|
0,51
|
0,34
|
0,22
|
0,18
|
0,14
|
0,12
|
0,10
|
|
0,5
|
0,51
|
0,34
|
0,22
|
0,18
|
0,14
|
0,12
|
0,10
|
|
|
0,9
|
0,51
|
0,33
|
0,21
|
0,16
|
0,12
|
0,10
|
0,09
|
|
|
10
|
0
|
0,44
|
0,29
|
0,18
|
0,14
|
0,11
|
0,10
|
0,09
|
|
0,5
|
0,44
|
0,29
|
0,18
|
0,14
|
0,11
|
0,10
|
0,09
|
|
|
0,9
|
0,44
|
0,28
|
0,17
|
0,12
|
0,10
|
0,08
|
0,07
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,58
|
0,38
|
0,22
|
0,17
|
0,12
|
0,09
|
0,08
|
|
0,5
|
0,62
|
0,38
|
0,22
|
0,17
|
0,12
|
0,09
|
0,08
|
|
|
0,9
|
0,66
|
0,43
|
0,26
|
0,18
|
0,12
|
0,09
|
0,08
|
|
|
5
|
0
|
0,44
|
0,27
|
0,16
|
0,12
|
0,08
|
0,07
|
0,06
|
|
0,5
|
0,46
|
0,27
|
0,16
|
0,12
|
0,08
|
0,07
|
0,06
|
|
|
0,9
|
0,52
|
0,30
|
0,17
|
0,13
|
0,09
|
0,07
|
0,06
|
|
|
10
|
0
|
0,37
|
0,23
|
0,12
|
0,09
|
0,07
|
0,06
|
0,05
|
|
0,5
|
0,39
|
0,24
|
0,13
|
0,09
|
0,07
|
0,06
|
0,05
|
|
|
0,9
|
0,42
|
0,25
|
0,14
|
0,10
|
0,07
|
0,06
|
0,05
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,51
|
0,30
|
0,14
|
0,10
|
0,06
|
0,04
|
0,03
|
|
0,5
|
0,57
|
0,32
|
0,17
|
0,11
|
0,07
|
0,05
|
0,04
|
|
|
0,9
|
0,63
|
0,39
|
0,22
|
0,14
|
0,09
|
0,06
|
0,05
|
|
|
5
|
0
|
0,38
|
0,20
|
0,10
|
0,07
|
0,04
|
0,03
|
0,02
|
|
0,5
|
0,41
|
0,22
|
0,11
|
0,07
|
0,04
|
0,03
|
0,02
|
|
|
0,9
|
0,48
|
0,27
|
0,14
|
0,10
|
0,06
|
0,04
|
0,03
|
|
|
10
|
0
|
0,31
|
0,17
|
0,08
|
0,05
|
0,03
|
0,025
|
0,02
|
|
0,5
|
0,34
|
0,18
|
0,09
|
0,06
|
0,04
|
0,025
|
0,02
|
|
|
0,9
|
0,39
|
0,22
|
0,11
|
0,07
|
0,045
|
0,03
|
0,02
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,45
|
0,22
|
0,09
|
0,05
|
0,025
|
0,015
|
0,01
|
|
0,5
|
0,52
|
0,25
|
0,11
|
0,06
|
0,03
|
0,02
|
0,01
|
|
|
0,9
|
0,60
|
0,35
|
0,18
|
0,11
|
0,06
|
0,04
|
0,03
|
|
|
5
|
0
|
0,31
|
0,14
|
0,06
|
0,03
|
0,015
|
0,01
|
0,007
|
|
0,5
|
0,36
|
0,17
|
0,08
|
0,04
|
0,02
|
0,01
|
0,007
|
|
|
0,9
|
0,45
|
0,24
|
0,11
|
0,07
|
0,04
|
0,02
|
0,015
|
|
|
10
|
0
|
0,24
|
0,11
|
0,04
|
0,02
|
0,01
|
0,008
|
0,005
|
|
0,5
|
0,29
|
0,13
|
0,05
|
0,03
|
0,01
|
0,008
|
0,005
|
|
|
0,9
|
0,36
|
0,19
|
0,09
|
0,05
|
0,03
|
0,02
|
0,01
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,32
|
0,11
|
0,02
|
0,008
|
0,002
|
0,001
|
0,000
|
|
0,5
|
0,43
|
0,15
|
0,04
|
0,01
|
0,004
|
0,002
|
0,001
|
|
|
0,9
|
0,56
|
0,29
|
0,12
|
0,07
|
0,03
|
0,015
|
0,007
|
|
|
5
|
0
|
0,20
|
0,06
|
0,009
|
0,003
|
0,001
|
0,000
|
0,000
|
|
0,5
|
0,27
|
0,09
|
0,02
|
0,006
|
0,002
|
0,001
|
0,000
|
|
|
0,9
|
0,39
|
0,18
|
0,07
|
0,03
|
0,01
|
0,005
|
0,002
|
|
|
10
|
0
|
0,14
|
0,04
|
0,006
|
0,002
|
0,001
|
0,000
|
0,000
|
|
0,5
|
0,18
|
0,06
|
0,01
|
0,003
|
0,001
|
0,000
|
0,000
|
|
|
0,9
|
0,30
|
0,13
|
0,05
|
0,02
|
0,006
|
0,003
|
0,001
|
|
Таблица А.3
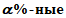 критические значения статистики Диксона (
D
2
N
)
критические значения статистики Диксона (
D
2
N
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,81
|
0,60
|
0,43
|
0,37
|
0,33
|
0,30
|
0,26
|
|
0,5
|
0,81
|
0,60
|
0,40
|
0,35
|
0,30
|
0,27
|
0,24
|
|
|
0,9
|
0,81
|
0,56
|
0,34
|
0,28
|
0,22
|
0,21
|
0,18
|
|
|
5
|
0
|
0,69
|
0,48
|
0,33
|
0,28
|
0,24
|
0,22
|
0,19
|
|
0,5
|
0,69
|
0,47
|
0,32
|
0,27
|
0,23
|
0,21
|
0,18
|
|
|
0,9
|
0,68
|
0,44
|
0,27
|
0,21
|
0,16
|
0,15
|
0,12
|
|
|
10
|
0
|
0,61
|
0,41
|
0,28
|
0,24
|
0,20
|
0,19
|
0,16
|
|
0,5
|
0,61
|
0,40
|
0,27
|
0,23
|
0,18
|
0,17
|
0,15
|
|
|
0,9
|
0,57
|
0,37
|
0,22
|
0,17
|
0,13
|
0,12
|
0,10
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,84
|
0,64
|
0,52
|
0,45
|
0,41
|
0,38
|
0,34
|
|
0,5
|
0,83
|
0,62
|
0,48
|
0,42
|
0,37
|
0,34
|
0,31
|
|
|
0,9
|
0,82
|
0,59
|
0,38
|
0,32
|
0,27
|
0,25
|
0,22
|
|
|
5
|
0
|
0,75
|
0,57
|
0,41
|
0,35
|
0,31
|
0,29
|
0,26
|
|
0,5
|
0,73
|
0,54
|
0,38
|
0,33
|
0,29
|
0,27
|
0,25
|
|
|
0,9
|
0,69
|
0,47
|
0,30
|
0,25
|
0,20
|
0,18
|
0,16
|
|
|
10
|
0
|
0,66
|
0,47
|
0,35
|
0,30
|
0,26
|
0,24
|
0,22
|
|
0,5
|
0,64
|
0,45
|
0,33
|
0,28
|
0,23
|
0,22
|
0,20
|
|
|
0,9
|
0,59
|
0,40
|
0,24
|
0,20
|
0,17
|
0,15
|
0,13
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,87
|
0,69
|
0,59
|
0,52
|
0,49
|
0,46
|
0,42
|
|
0,5
|
0,87
|
0,69
|
0,54
|
0,49
|
0,44
|
0,42
|
0,39
|
|
|
0,9
|
0,84
|
0,61
|
0,44
|
0,38
|
0,34
|
0,32
|
0,28
|
|
|
5
|
0
|
0,77
|
0,59
|
0,47
|
0,41
|
0,37
|
0,35
|
0,32
|
|
0,5
|
0,76
|
0,57
|
0,44
|
0,39
|
0,34
|
0,32
|
0,29
|
|
|
0,9
|
0,70
|
0,50
|
0,33
|
0,28
|
0,24
|
0,22
|
0,20
|
|
|
10
|
0
|
0,70
|
0,52
|
0,40
|
0,36
|
0,32
|
0,30
|
0,27
|
|
0,5
|
0,67
|
0,49
|
0,38
|
0,33
|
0,29
|
0,27
|
0,24
|
|
|
0,9
|
0,61
|
0,42
|
0,27
|
0,23
|
0,20
|
0,19
|
0,16
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,89
|
0,75
|
0,65
|
0,58
|
0,55
|
0,52
|
0,48
|
|
0,5
|
0,89
|
0,73
|
0,61
|
0,57
|
0,51
|
0,48
|
0,45
|
|
|
0,9
|
0,85
|
0,64
|
0,49
|
0,44
|
0,39
|
0,36
|
0,32
|
|
|
5
|
0
|
0,81
|
0,65
|
0,53
|
0,47
|
0,43
|
0,40
|
0,37
|
|
0,5
|
0,79
|
0,62
|
0,51
|
0,45
|
0,39
|
0,37
|
0,34
|
|
|
0,9
|
0,72
|
0,53
|
0,37
|
0,32
|
0,28
|
0,26
|
0,24
|
|
|
10
|
0
|
0,74
|
0,57
|
0,46
|
0,41
|
0,37
|
0,35
|
0,32
|
|
0,5
|
0,71
|
0,55
|
0,44
|
0,39
|
0,34
|
0,32
|
0,29
|
|
|
0,9
|
0,64
|
0,46
|
0,31
|
0,27
|
0,22
|
0,21
|
0,19
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,91
|
0,79
|
0,7
|
0,64
|
0,61
|
0,58
|
0,53
|
|
0,5
|
0,91
|
0,78
|
0,67
|
0,61
|
0,56
|
0,54
|
0,50
|
|
|
0,9
|
0,88
|
0,68
|
0,53
|
0,48
|
0,42
|
0,40
|
0,37
|
|
|
5
|
0
|
0,84
|
0,70
|
0,58
|
0,52
|
0,48
|
0,46
|
0,42
|
|
0,5
|
0,83
|
0,68
|
0,56
|
0,50
|
0,45
|
0,43
|
0,39
|
|
|
0,9
|
0,75
|
0,59
|
0,42
|
0,37
|
0,32
|
0,31
|
0,28
|
|
|
10
|
0
|
0,77
|
0,62
|
0,52
|
0,46
|
0,41
|
0,39
|
0,36
|
|
0,5
|
0,76
|
0,60
|
0,50
|
0,44
|
0,39
|
0,37
|
0,33
|
|
|
0,9
|
0,67
|
0,49
|
0,36
|
0,31
|
0,27
|
0,26
|
0,23
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,97
|
0,88
|
0,80
|
0,75
|
0,71
|
0,68
|
0,63
|
|
0,5
|
0,97
|
0,88
|
0,76
|
0,72
|
0,66
|
0,64
|
0,60
|
|
|
0,9
|
0,94
|
0,84
|
0,69
|
0,63
|
0,56
|
0,53
|
0,49
|
|
|
5
|
0
|
0,91
|
0,79
|
0,69
|
0,62
|
0,58
|
0,55
|
0,50
|
|
0,5
|
0,91
|
0,78
|
0,67
|
0,60
|
0,55
|
0,52
|
0,47
|
|
|
0,9
|
0,84
|
0,70
|
0,54
|
0,48
|
0,42
|
0,39
|
0,36
|
|
|
10
|
0
|
0,85
|
0,72
|
0,62
|
0,56
|
0,50
|
0,47
|
0,44
|
|
0,5
|
0,84
|
0,71
|
0,60
|
0,54
|
0,47
|
0,45
|
0,42
|
|
|
0,9
|
0,76
|
0,60
|
0,46
|
0,40
|
0,36
|
0,33
|
0,30
|
|
Таблица А.4
 критические значения статистики Диксона (
D
2
I
)
критические значения статистики Диксона (
D
2
I
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,81
|
0,60
|
0,43
|
0,37
|
0,29
|
0,25
|
0,22
|
|
0,5
|
0,81
|
0,60
|
0,41
|
0,35
|
0,28
|
0,34
|
0,21
|
|
|
0,9
|
0,84
|
0,57
|
0,36
|
0,28
|
0,22
|
0,20
|
0,18
|
|
|
5
|
0
|
0,69
|
0,48
|
0,33
|
0,28
|
0,22
|
0,19
|
0,17
|
|
0,5
|
0,69
|
0,47
|
0,31
|
0,26
|
0,21
|
0,18
|
0,16
|
|
|
0,9
|
0,68
|
0,41
|
0,26
|
0,20
|
0,16
|
0,14
|
0,12
|
|
|
10
|
0
|
0,61
|
0,41
|
0,28
|
0,24
|
0,18
|
0,16
|
0,14
|
|
0,5
|
0,61
|
0,40
|
0,27
|
0,23
|
0,17
|
0,15
|
0,13
|
|
|
0,9
|
0,58
|
0,35
|
0,22
|
0,17
|
0,13
|
0,11
|
0,10
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,79
|
0,54
|
0,35
|
0,28
|
0,21
|
0,18
|
0,15
|
|
0,5
|
0,79
|
0,54
|
0,34
|
0,27
|
0,21
|
0,18
|
0,15
|
|
|
0,9
|
0,79
|
0,54
|
0,33
|
0,24
|
0,17
|
0,15
|
0,14
|
|
|
5
|
0
|
0,65
|
0,43
|
0,26
|
0,20
|
0,19
|
0,14
|
0,12
|
|
0,5
|
0,65
|
0,41
|
0,25
|
0,19
|
0,15
|
0,13
|
0,11
|
|
|
0,9
|
0,65
|
0,38
|
0,23
|
0,17
|
0,13
|
0,11
|
0,09
|
|
|
10
|
0
|
0,57
|
0,36
|
0,22
|
0,17
|
0,13
|
0,11
|
0,10
|
|
0,5
|
0,57
|
0,35
|
0,21
|
0,16
|
0,13
|
0,11
|
0,10
|
|
|
0,9
|
0,56
|
0,33
|
0,19
|
0,14
|
0,10
|
0,08
|
0,07
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,76
|
0,47
|
0,27
|
0,19
|
0,14
|
0,11
|
0,09
|
|
0,5
|
0,78
|
0,49
|
0,27
|
0,19
|
0,14
|
0,11
|
0,09
|
|
|
0,9
|
0,32
|
0,51
|
0,29
|
0,19
|
0,14
|
0,11
|
0,09
|
|
|
5
|
0
|
0,60
|
0,36
|
0,19
|
0,14
|
0,10
|
0,08
|
0,07
|
|
0,5
|
0,62
|
0,36
|
0,19
|
0,14
|
0,10
|
0,08
|
0,07
|
|
|
0,9
|
0,64
|
0,37
|
0,20
|
0,14
|
0,10
|
0,08
|
0,07
|
|
|
10
|
0
|
0,52
|
0,30
|
0,15
|
0,11
|
0,08
|
0,07
|
0,06
|
|
0,5
|
0,53
|
0,30
|
0,15
|
0,11
|
0,08
|
0,07
|
0,06
|
|
|
0,9
|
0,54
|
0,30
|
0,16
|
0,11
|
0,08
|
0,07
|
0,06
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,73
|
0,39
|
0,20
|
0,12
|
0,07
|
0,05
|
0,04
|
|
0,5
|
0,76
|
0,42
|
0,21
|
0,13
|
0,08
|
0,06
|
0,04
|
|
|
0,9
|
0,80
|
0,47
|
0,25
|
0,16
|
0,10
|
0,07
|
0,05
|
|
|
5
|
0
|
0,55
|
0,28
|
0,12
|
0,08
|
0,05
|
0,04
|
0,03
|
|
0,5
|
0,57
|
0,29
|
0,14
|
0,08
|
0,05
|
0,04
|
0,03
|
|
|
0,9
|
0,62
|
0,33
|
0,16
|
0,11
|
0,06
|
0,05
|
0,04
|
|
|
10
|
0
|
0,46
|
0,23
|
0,10
|
0,07
|
0,04
|
0,08
|
0,02
|
|
0,5
|
0,48
|
0,24
|
0,11
|
0,07
|
0,04
|
0,03
|
0,02
|
|
|
0,9
|
0,52
|
0,27
|
0,13
|
0,08
|
0,05
|
0,04
|
0,03
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,68
|
0,32
|
0,13
|
0,06
|
0,03
|
0,02
|
0,01
|
|
0,5
|
0,73
|
0,35
|
0,14
|
0,07
|
0,04
|
0,02
|
0,015
|
|
|
0,9
|
0,78
|
0,44
|
0,20
|
0,13
|
0,07
|
0,04
|
0,03
|
|
|
5
|
0
|
0,49
|
0,21
|
0,08
|
0,04
|
0,02
|
0,01
|
0,008
|
|
0,5
|
0,52
|
0,23
|
0,08
|
0,04
|
0,02
|
0,01
|
0,52
|
|
|
0,9
|
0,60
|
0,29
|
0,13
|
0,08
|
0,04
|
0,03
|
0,02
|
|
|
10
|
0
|
0,39
|
0,16
|
0,05
|
0,03
|
0,015
|
0,01
|
0,006
|
|
0,5
|
0,43
|
0,19
|
0,06
|
0,03
|
0,015
|
0,01
|
0,006
|
|
|
0,9
|
0,49
|
0,24
|
0,10
|
0,06
|
0,03
|
0,02
|
0,01
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,57
|
0,18
|
0,03
|
0,01
|
0,003
|
0,001
|
0,001
|
|
0,5
|
0,66
|
0,23
|
0,06
|
0,02
|
0,005
|
0,002
|
0,001
|
|
|
0,9
|
0,79
|
0,39
|
0,13
|
0,08
|
0,03
|
0,015
|
0,009
|
|
|
5
|
0
|
0,37
|
0,10
|
0,01
|
0,005
|
0,001
|
0,001
|
0
|
|
0,5
|
0,42
|
0,13
|
0,02
|
0,008
|
0,002
|
0,001
|
0
|
|
|
0,9
|
0,55
|
0,23
|
0,09
|
0,04
|
0,01
|
0,006
|
0,003
|
|
|
10
|
0
|
0,23
|
0,06
|
0,008
|
0,003
|
0,001
|
0
|
0
|
|
0,5
|
0,32
|
0,09
|
0,015
|
0,005
|
0,001
|
0
|
0
|
|
|
0,9
|
0,44
|
0,17
|
0,06
|
0,025
|
0,007
|
0,003
|
0,001
|
|
Таблица А.5
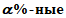 критические значения статистики Диксона (
D
3
N
)
критические значения статистики Диксона (
D
3
N
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,95
|
0,73
|
0,51
|
0,43
|
0,36
|
0,34
|
0,30
|
|
0,5
|
0,94
|
0,72
|
0,49
|
0,40
|
0,34
|
0,31
|
0,28
|
|
|
0,9
|
0,94
|
0,71
|
0,45
|
0,37
|
0,30
|
0,26
|
0,22
|
|
|
5
|
0
|
0,88
|
0,61
|
0,42
|
0,36
|
0,30
|
0,27
|
0,24
|
|
0,5
|
0,88
|
0,61
|
0,41
|
0,35
|
0,28
|
0,25
|
0,22
|
|
|
0,9
|
0,87
|
0,59
|
0,35
|
0,28
|
0,22
|
0,20
|
0,17
|
|
|
10
|
0
|
0,82
|
0,55
|
0,37
|
0,31
|
0,26
|
0,24
|
0,21
|
|
0,5
|
0,82
|
0,54
|
0,36
|
0,30
|
0,25
|
0,23
|
0,20
|
|
|
0,9
|
0,81
|
0,53
|
0,30
|
0,24
|
0,19
|
0,17
|
0,14
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,95
|
0,76
|
0,58
|
0,52
|
0,45
|
0,43
|
0,38
|
|
0,5
|
0,95
|
0,76
|
0,56
|
0,49
|
0,42
|
0,40
|
0,36
|
|
|
0,9
|
0,94
|
0,75
|
0,49
|
0,39
|
0,33
|
0,31
|
0,27
|
|
|
5
|
0
|
0,89
|
0,66
|
0,50
|
0,43
|
0,38
|
0,34
|
0,31
|
|
0,5
|
0,89
|
0,65
|
0,47
|
0,41
|
0,35
|
0,34
|
0,29
|
|
|
0,9
|
0,87
|
0,62
|
0,38
|
0,32
|
0,26
|
0,24
|
0,21
|
|
|
10
|
0
|
0,85
|
0,61
|
0,45
|
0,39
|
0,33
|
0,30
|
0,28
|
|
0,5
|
0,84
|
0,59
|
0,43
|
0,37
|
0,31
|
0,28
|
0,26
|
|
|
0,9
|
0,82
|
0,55
|
0,34
|
0,28
|
0,22
|
0,21
|
0,18
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,96
|
0,80
|
0,64
|
0,60
|
0,53
|
0,50
|
0,46
|
|
0,5
|
0,96
|
0,80
|
0,62
|
0,57
|
0,50
|
0,47
|
0,44
|
|
|
0,9
|
0,95
|
0,77
|
0,53
|
0,46
|
0,38
|
0,36
|
0,33
|
|
|
5
|
0
|
0,91
|
0,71
|
0,56
|
0,50
|
0,45
|
0,41
|
0,38
|
|
0,5
|
0,90
|
0,70
|
0,54
|
0,49
|
0,43
|
0,40
|
0,36
|
|
|
0,9
|
0,88
|
0,64
|
0,43
|
0,37
|
0,31
|
0,29
|
0,26
|
|
|
10
|
0
|
0,87
|
0,66
|
0,51
|
0,46
|
0,40
|
0,36
|
0,34
|
|
0,5
|
0,86
|
0,64
|
0,49
|
0,43
|
0,37
|
0,33
|
0,31
|
|
|
0,9
|
0,84
|
0,58
|
0,38
|
0,32
|
0,27
|
0,25
|
0,22
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,96
|
0,84
|
0,70
|
0,66
|
0,60
|
0,58
|
0,54
|
|
0,5
|
0,96
|
0,84
|
0,68
|
0,63
|
0,56
|
0,53
|
0,50
|
|
|
0,9
|
0,96
|
0,80
|
0,60
|
0,54
|
0,46
|
0,43
|
0,39
|
|
|
5
|
0
|
0,93
|
0,76
|
0,63
|
0,57
|
0,51
|
0,48
|
0,44
|
|
0,5
|
0,92
|
0,74
|
0,61
|
0,55
|
0,49
|
0,46
|
0,42
|
|
|
0,9
|
0,89
|
0,67
|
0,74
|
0,41
|
0,36
|
0,33
|
0,30
|
|
|
10
|
0
|
0,89
|
0,71
|
0,58
|
0,82
|
0,46
|
0,42
|
0,40
|
|
0,5
|
0,88
|
0,69
|
0,54
|
0,49
|
0,43
|
0,39
|
0,37
|
|
|
0,9
|
0,85
|
0,62
|
0,42
|
0,36
|
0,30
|
0,30
|
0,27
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,97
|
0,88
|
0,76
|
0,71
|
0,66
|
0,63
|
0,59
|
|
0,5
|
0,97
|
0,87
|
0,74
|
0,68
|
0,63
|
0,60
|
0,56
|
|
|
0,9
|
0,96
|
0,85
|
0,66
|
0,59
|
0,52
|
0,49
|
0,45
|
|
|
5
|
0
|
0,94
|
0,80
|
0,68
|
0,63
|
0,57
|
0,54
|
0,50
|
|
0,5
|
0,94
|
0,79
|
0,66
|
0,61
|
0,54
|
0,51
|
0,47
|
|
|
0,9
|
0,91
|
0,72
|
0,53
|
0,46
|
0,41
|
0,38
|
0,35
|
|
|
10
|
0
|
0,92
|
0,77
|
0,63
|
0,58
|
0,52
|
0,48
|
0,46
|
|
0,5
|
0,91
|
0,74
|
0,60
|
0,55
|
0,49
|
0,45
|
0,42
|
|
|
0,9
|
0,87
|
0,66
|
0,48
|
0,41
|
0,36
|
0,33
|
0,30
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,99
|
0,95
|
0,86
|
0,82
|
0,76
|
0,73
|
0,68
|
|
0,5
|
0,99
|
0,95
|
0,86
|
0,82
|
0,74
|
0,70
|
0,65
|
|
|
0,9
|
0,99
|
0,94
|
0,83
|
0,75
|
0,64
|
0,61
|
0,57
|
|
|
5
|
0
|
0,98
|
0,89
|
0,79
|
0,73
|
0,67
|
0,63
|
0,59
|
|
0,5
|
0,98
|
0,89
|
0,77
|
0,72
|
0,65
|
0,61
|
0,56
|
|
|
0,9
|
0,96
|
0,85
|
0,69
|
0,60
|
0,52
|
0,50
|
0,46
|
|
|
10
|
0
|
0,96
|
0,85
|
0,75
|
0,69
|
0,62
|
0,58
|
0,54
|
|
0,5
|
0,96
|
0,84
|
0,72
|
0,66
|
0,59
|
0,55
|
0,51
|
|
|
0,9
|
0,92
|
0,78
|
0,61
|
0,53
|
0,46
|
0,44
|
0,41
|
|
Таблица А.6
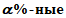 критические значения статистики Диксона (
D
3
I
)
критические значения статистики Диксона (
D
3
I
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,95
|
0,73
|
0,51
|
0,43
|
0,32
|
0,30
|
0,26
|
|
0,5
|
0,95
|
0,72
|
0,49
|
0,40
|
0,30
|
0,28
|
0,25
|
|
|
0,9
|
0,95
|
0,70
|
0,45
|
0,37
|
0,28
|
0,25
|
0,24
|
|
|
5
|
0
|
0,87
|
0,61
|
0,42
|
0,36
|
0,28
|
0,24
|
0,22
|
|
0,5
|
0,87
|
0,61
|
0,41
|
0,35
|
0,27
|
0,23
|
0,20
|
|
|
0,9
|
0,87
|
0,59
|
0,37
|
0,29
|
0,22
|
0,20
|
0,17
|
|
|
10
|
0
|
0,82
|
0,55
|
0,37
|
0,31
|
0,25
|
0,21
|
0,19
|
|
0,5
|
0,82
|
0,55
|
0,36
|
0,30
|
0,24
|
0,20
|
0,18
|
|
|
0,9
|
0,82
|
0,52
|
0,32
|
0,24
|
0,19
|
0,16
|
0,14
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,92
|
0,67
|
0,42
|
0,33
|
0,24
|
0,22
|
0,19
|
|
0,5
|
0,92
|
0,67
|
0,41
|
0,32
|
0,23
|
0,21
|
0,18
|
|
|
0,9
|
0,95
|
0,67
|
0,41
|
0,32
|
0,23
|
0,21
|
0,18
|
|
|
5
|
0
|
0,87
|
0,56
|
0,34
|
0,27
|
0,20
|
0,17
|
0,15
|
|
0,5
|
0,87
|
0,56
|
0,34
|
0,25
|
0,20
|
0,17
|
0,15
|
|
|
0,9
|
0,87
|
0,56
|
0,33
|
0,24
|
0,17
|
0,15
|
0,13
|
|
|
10
|
0
|
0,80
|
0,51
|
0,30
|
0,23
|
0,18
|
0,15
|
0,13
|
|
0,5
|
0,80
|
0,51
|
0,29
|
0,22
|
0,18
|
0,15
|
0,13
|
|
|
0,9
|
0,8
|
0,49
|
0,28
|
0,2
|
0,15
|
0,13
|
0,1
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,91
|
0,61
|
0,33
|
0,24
|
0,16
|
0,14
|
0,10
|
|
0,5
|
0,92
|
0,62
|
0,34
|
0,25
|
0,17
|
0,14
|
0,10
|
|
|
0,9
|
0,95
|
0,64
|
0,37
|
0,23
|
0,18
|
0,15
|
0,12
|
|
|
5
|
0
|
0,83
|
0,49
|
0,26
|
0,19
|
0,13
|
0,10
|
0,09
|
|
0,5
|
0,84
|
0,52
|
0,27
|
0,19
|
0,13
|
0,10
|
0,09
|
|
|
0,9
|
0,87
|
0,53
|
0,28
|
0,20
|
0,14
|
0,11
|
0,09
|
|
|
10
|
0
|
0,77
|
0,44
|
0,23
|
0,16
|
0,11
|
0,09
|
0,08
|
|
0,5
|
0,78
|
0,44
|
0,23
|
0,16
|
0,11
|
0,09
|
0,08
|
|
|
0,9
|
0,80
|
0,46
|
0,24
|
0,16
|
0,11
|
0,09
|
0,08
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,90
|
0,53
|
0,23
|
0,16
|
0,10
|
0,07
|
0,05
|
|
0,5
|
0,90
|
0,57
|
0,26
|
0,17
|
0,11
|
0,08
|
0,06
|
|
|
0,9
|
0,95
|
0,62
|
0,34
|
0,23
|
0,13
|
0,10
|
0,08
|
|
|
5
|
0
|
0,80
|
0,42
|
0,18
|
0,11
|
0,07
|
0,05
|
0,04
|
|
0,5
|
0,82
|
0,46
|
0,20
|
0,12
|
0,08
|
0,05
|
0,04
|
|
|
0,9
|
0,85
|
0,49
|
0,24
|
0,16
|
0,10
|
0,07
|
0,06
|
|
|
10
|
0
|
0,74
|
0,37
|
0,16
|
0,10
|
0,06
|
0,04
|
0,03
|
|
0,5
|
0,75
|
0,38
|
0,16
|
0,10
|
0,06
|
0,04
|
0,03
|
|
|
0,9
|
0,78
|
0,43
|
0,20
|
0,13
|
0,08
|
0,06
|
0,04
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,88
|
0,47
|
0,17
|
0,09
|
0,045
|
0,03
|
0,02
|
|
0,5
|
0,89
|
0,52
|
0,20
|
0,10
|
0,05
|
0,03
|
0,02
|
|
|
0,9
|
0,94
|
0,59
|
0,30
|
0,19
|
0,10
|
0,07
|
0,055
|
|
|
5
|
0
|
0,78
|
0,35
|
0,11
|
0,06
|
0,03
|
0,02
|
0,01
|
|
0,5
|
0,79
|
0,33
|
0,14
|
0,07
|
0,03
|
0,02
|
0,01
|
|
|
0,9
|
0,84
|
0,47
|
0,20
|
0,12
|
0,065
|
0,04
|
0,03
|
|
|
10
|
0
|
0,69
|
0,29
|
0,10
|
0,05
|
0,025
|
0,015
|
0,01
|
|
0,5
|
0,72
|
0,32
|
0,11
|
0,06
|
0,03
|
0,02
|
0,01
|
|
|
0,9
|
0,77
|
0,39
|
0,16
|
0,10
|
0,05
|
0,03
|
0,02
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,84
|
0,33
|
0,06
|
0,02
|
0,006
|
0,002
|
0,001
|
|
0,5
|
0,87
|
0,42
|
0,10
|
0,03
|
0,008
|
0,004
|
0,002
|
|
|
0,9
|
0,94
|
0,52
|
0,23
|
0,12
|
0,05
|
0,025
|
0,015
|
|
|
5
|
0
|
0,70
|
0,21
|
0,03
|
0,01
|
0,003
|
0,001
|
0,001
|
|
0,5
|
0,73
|
0,27
|
0,05
|
0,015
|
0,004
|
0,002
|
0,001
|
|
|
0,9
|
0,81
|
0,40
|
0,14
|
0,07
|
0,02
|
0,01
|
0,006
|
|
|
10
|
0
|
0,59
|
0,15
|
0,02
|
0,008
|
0,002
|
0,001
|
0
|
|
0,5
|
0,63
|
0,20
|
0,03
|
0,01
|
0,003
|
0,001
|
0
|
|
|
0,9
|
0,73
|
0,31
|
0,10
|
0,05
|
0,015
|
0,007
|
0,003
|
|
Таблица А.7
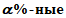 критические значения статистики Диксона (
D
4
N
)
критические значения статистики Диксона (
D
4
N
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,997
|
0,79
|
0,54
|
0,46
|
0,39
|
0,36
|
0,31
|
|
0,5
|
0,996
|
0,79
|
0,52
|
0,44
|
0,36
|
0,32
|
0,28
|
|
|
0,9
|
0,995
|
0,77
|
0,48
|
0,40
|
0,30
|
0,26
|
0,23
|
|
|
5
|
0
|
0,98
|
0,68
|
0,45
|
0,38
|
0,32
|
0,28
|
0,25
|
|
0,5
|
0,98
|
0,68
|
0,44
|
0,37
|
0,30
|
0,26
|
0,23
|
|
|
0,9
|
0,97
|
0,65
|
0,38
|
0,29
|
0,22
|
0,21
|
0,18
|
|
|
10
|
0
|
0,96
|
0,62
|
0,40
|
0,33
|
0,28
|
0,25
|
0,22
|
|
0,5
|
0,96
|
0,61
|
0,39
|
0,32
|
0,26
|
0,23
|
0,20
|
|
|
0,9
|
0,95
|
0,58
|
0,33
|
0,26
|
0,20
|
0,18
|
0,15
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,997
|
0,82
|
0,60
|
0,54
|
0,47
|
0,44
|
0,39
|
|
0,5
|
0,997
|
0,82
|
0,58
|
0,52
|
0,44
|
0,41
|
0,37
|
|
|
0,9
|
0,995
|
0,79
|
0,51
|
0,44
|
0,35
|
0,32
|
0,27
|
|
|
5
|
0
|
0,98
|
0,72
|
0,53
|
0,45
|
0,39
|
0,35
|
0,32
|
|
0,5
|
0,98
|
0,71
|
0,50
|
0,43
|
0,37
|
0,33
|
0,30
|
|
|
0,9
|
0,97
|
0,67
|
0,41
|
0,33
|
0,27
|
0,25
|
0,22
|
|
|
10
|
0
|
0,96
|
0,67
|
0,46
|
0,40
|
0,34
|
0,31
|
0,28
|
|
0,5
|
0,96
|
0,65
|
0,44
|
0,38
|
0,32
|
0,29
|
0,26
|
|
|
0,9
|
0,95
|
0,60
|
0,36
|
0,29
|
0,23
|
0,21
|
0,19
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,998
|
0,85
|
0,67
|
0,60
|
0,54
|
0,51
|
0,47
|
|
0,5
|
0,997
|
0,84
|
0,64
|
0,58
|
0,50
|
0,48
|
0,44
|
|
|
0,9
|
0,995
|
0,81
|
0,55
|
0,48
|
0,40
|
0,37
|
0,33
|
|
|
5
|
0
|
0,98
|
0,76
|
0,59
|
0,52
|
0,46
|
0,42
|
0,39
|
|
0,5
|
0,98
|
0,75
|
0,56
|
0,49
|
0,43
|
0,39
|
0,36
|
|
|
0,9
|
0,98
|
0,70
|
0,46
|
0,39
|
0,33
|
0,30
|
0,27
|
|
|
10
|
0
|
0,97
|
0,71
|
0,53
|
0,47
|
0,41
|
0,37
|
0,35
|
|
0,5
|
0,96
|
0,69
|
0,50
|
0,44
|
0,38
|
0,34
|
0,32
|
|
|
0,9
|
0,95
|
0,63
|
0,39
|
0,33
|
0,28
|
0,26
|
0,23
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,998
|
0,87
|
0,72
|
0,66
|
0,61
|
0,58
|
0,54
|
|
0,5
|
0,998
|
0,86
|
0,70
|
0,63
|
0,57
|
0,54
|
0,50
|
|
|
0,9
|
0,996
|
0,83
|
0,60
|
0,53
|
0,46
|
0,43
|
0,38
|
|
|
5
|
0
|
0,98
|
0,79
|
0,65
|
0,58
|
0,52
|
0,48
|
0,45
|
|
0,5
|
0,98
|
0,78
|
0,61
|
0,55
|
0,49
|
0,46
|
0,42
|
|
|
0,9
|
0,98
|
0,72
|
0,50
|
0,43
|
0,37
|
0,35
|
0,31
|
|
|
10
|
0
|
0,97
|
0,75
|
0,58
|
0,52
|
0,46
|
0,43
|
0,40
|
|
0,5
|
0,97
|
0,73
|
0,56
|
0,50
|
0,44
|
0,41
|
0,37
|
|
|
0,9
|
0,96
|
0,65
|
0,44
|
0,38
|
0,33
|
0,30
|
0,27
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,998
|
0,90
|
0,76
|
0,71
|
0,66
|
0,63
|
0,59
|
|
0,5
|
0,998
|
0,89
|
0,75
|
0,69
|
0,63
|
0,60
|
0,56
|
|
|
0,9
|
0,997
|
0,88
|
0,67
|
0,60
|
0,51
|
0,49
|
0,45
|
|
|
5
|
0
|
0,988
|
0,83
|
0,70
|
0,63
|
0,57
|
0,54
|
0,50
|
|
0,5
|
0,988
|
0,82
|
0,67
|
0,60
|
0,54
|
0,51
|
0,47
|
|
|
0,9
|
0,98
|
0,76
|
0,54
|
0,47
|
0,41
|
0,38
|
0,35
|
|
|
10
|
0
|
0,98
|
0,79
|
0,64
|
0,58
|
0,52
|
0,49
|
0,46
|
|
0,5
|
0,98
|
0,77
|
0,61
|
0,55
|
0,49
|
0,45
|
0,42
|
|
|
0,9
|
0,96
|
0,70
|
0,48
|
0,42
|
0,36
|
0,33
|
0,31
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,999
|
0,94
|
0,85
|
0,81
|
0,76
|
0,73
|
0,68
|
|
0,5
|
0,999
|
0,94
|
0,85
|
0,81
|
0,74
|
0,70
|
0,65
|
|
|
0,9
|
0,999
|
0,94
|
0,83
|
0,77
|
0,67
|
0,62
|
0,57
|
|
|
5
|
0
|
0,994
|
0,90
|
0,8
|
0,73
|
0,67
|
0,63
|
0,59
|
|
0,5
|
0,994
|
0,90
|
0,78
|
0,71
|
0,65
|
0,61
|
0,57
|
|
|
0,9
|
0,988
|
0,87
|
0,70
|
0,60
|
0,52
|
0,50
|
0,46
|
|
|
10
|
0
|
0,986
|
0,86
|
0,75
|
0,69
|
0,62
|
0,58
|
0,54
|
|
0,5
|
0,986
|
0,85
|
0,72
|
0,66
|
0,60
|
0,56
|
0,52
|
|
|
0,9
|
0,98
|
0,80
|
0,61
|
0,53
|
0,47
|
0,44
|
0,41
|
|
Таблица А.8
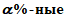 критические значения статистики Диксона (
D
4
I
)
критические значения статистики Диксона (
D
4
I
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,997
|
0,79
|
0,54
|
0,46
|
0,35
|
0,31
|
0,27
|
|
0,5
|
0,996
|
0,78
|
0,52
|
0,44
|
0,34
|
0,30
|
0,26
|
|
|
0,9
|
0,994
|
0,74
|
0,47
|
0,39
|
0,29
|
0,27
|
0,24
|
|
|
5
|
0
|
0,98
|
0,68
|
0,45
|
0,38
|
0,30
|
0,26
|
0,23
|
|
0,5
|
0,98
|
0,68
|
0,44
|
0,35
|
0,28
|
0,24
|
0,21
|
|
|
0,9
|
0,98
|
0,64
|
0,40
|
0,30
|
0,22
|
0,20
|
0,18
|
|
|
10
|
0
|
0,96
|
0,62
|
0,40
|
0,33
|
0,26
|
0,22
|
0,20
|
|
0,5
|
0,96
|
0,62
|
0,39
|
0,31
|
0,25
|
0,21
|
0,19
|
|
|
0,9
|
0,96
|
0,53
|
0,34
|
0,25
|
0,20
|
0,17
|
0,15
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,996
|
0,75
|
0,47
|
0,35
|
0,27
|
0,23
|
0,19
|
|
0,5
|
0,996
|
0,75
|
0,46
|
0,35
|
0,27
|
0,23
|
0,19
|
|
|
0,9
|
0,993
|
0,72
|
0,44
|
0,34
|
0,24
|
0,21
|
0,18
|
|
|
5
|
0
|
0,98
|
0,64
|
0,38
|
0,30
|
0,22
|
0,18
|
0,16
|
|
0,5
|
0,98
|
0,64
|
0,38
|
0,28
|
0,21
|
0,17
|
0,15
|
|
|
0,9
|
0,97
|
0,62
|
0,36
|
0,26
|
0,18
|
0,16
|
0,14
|
|
|
10
|
0
|
0,95
|
0,58
|
0,34
|
0,25
|
0,20
|
0,16
|
0,14
|
|
0,5
|
0,95
|
0,58
|
0,32
|
0,24
|
0,19
|
0,15
|
0,13
|
|
|
0,9
|
0,95
|
0,55
|
0,30
|
0,22
|
0,16
|
0,13
|
0,11
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,996
|
0,70
|
0,38
|
0,26
|
0,18
|
0,15
|
0,11
|
|
0,5
|
0,996
|
0,70
|
0,38
|
0,26
|
0,18
|
0,15
|
0,11
|
|
|
0,9
|
0,998
|
0,70
|
0,40
|
0,30
|
0,20
|
0,17
|
0,14
|
|
|
5
|
0
|
0,97
|
0,60
|
0,30
|
0,20
|
0,14
|
0,11
|
0,09
|
|
0,5
|
0,97
|
0,60
|
0,30
|
0,20
|
0,14
|
0,11
|
0,09
|
|
|
0,9
|
0,97
|
0,60
|
0,32
|
0,22
|
0,14
|
0,11
|
0,09
|
|
|
10
|
0
|
0,95
|
0,52
|
0,26
|
0,18
|
0,13
|
0,10
|
0,08
|
|
0,5
|
0,95
|
0,52
|
0,26
|
0,18
|
0,13
|
0,10
|
0,08
|
|
|
0,9
|
0,95
|
0,52
|
0,27
|
0,18
|
0,13
|
0,10
|
0,08
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,996
|
0,65
|
0,29
|
0,18
|
0,10
|
0,08
|
0,05
|
|
0,5
|
0,996
|
0,68
|
0,30
|
0,19
|
0,11
|
0,09
|
0,06
|
|
|
0,9
|
0,992
|
0,69
|
0,37
|
0,25
|
0,14
|
0,11
|
0,08
|
|
|
5
|
0
|
0,97
|
0,53
|
0,21
|
0,14
|
0,09
|
0,06
|
0,04
|
|
0,5
|
0,97
|
0,54
|
0,23
|
0,15
|
0,10
|
0,06
|
0,04
|
|
|
0,9
|
0,97
|
0,56
|
0,27
|
0,17
|
0,11
|
0,08
|
0,06
|
|
|
10
|
0
|
0,94
|
0,44
|
0,18
|
0,12
|
0,08
|
0,05
|
0,08
|
|
0,5
|
0,94
|
0,46
|
0,19
|
0,13
|
0,09
|
0,06
|
0,04
|
|
|
0,9
|
0,95
|
0,49
|
0,23
|
0,14
|
0,10
|
0,07
|
0,05
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,995
|
0,59
|
0,21
|
0,11
|
0,05
|
0,03
|
0,02
|
|
0,5
|
0,995
|
0,64
|
0,22
|
0,12
|
0,06
|
0,04
|
0,02
|
|
|
0,9
|
0,992
|
0,64
|
0,32
|
0,20
|
0,11
|
0,08
|
0,06
|
|
|
5
|
0
|
0,96
|
0,45
|
0,14
|
0,075
|
0,035
|
0,02
|
0,015
|
|
0,5
|
0,96
|
0,48
|
0,16
|
0,08
|
0,04
|
0,025
|
0,015
|
|
|
0,9
|
0,97
|
0,53
|
0,23
|
0,13
|
0,07
|
0,045
|
0,03
|
|
|
10
|
0
|
0,93
|
0,37
|
0,11
|
0,06
|
0,03
|
0,02
|
0,01
|
|
0,5
|
0,93
|
0,40
|
0,13
|
0,07
|
0,03
|
0,02
|
0,01
|
|
|
0,9
|
0,94
|
0,46
|
0,18
|
0,11
|
0,055
|
0,035
|
0,02
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,993
|
0,480
|
0,090
|
0,025
|
0,008
|
0,030
|
0,001
|
|
0,5
|
0,994
|
0,550
|
0,110
|
0,035
|
0,010
|
0,005
|
0,002
|
|
|
0,9
|
0,997
|
0,580
|
0,220
|
0,120
|
0,055
|
0,030
|
0,020
|
|
|
5
|
0
|
0,940
|
0,300
|
0,040
|
0,015
|
0,004
|
0,001
|
0,0010
|
|
0,5
|
0,950
|
0,360
|
0,060
|
0,020
|
0,006
|
0,002
|
0,001
|
|
|
0,9
|
0,970
|
0,470
|
0,160
|
0,080
|
0,030
|
0,015
|
0,006
|
|
|
10
|
0
|
0,900
|
0,230
|
0,030
|
0,010
|
0,002
|
0,001
|
0
|
|
0,5
|
0,910
|
0,280
|
0,040
|
0,010
|
0,004
|
0,001
|
0,001
|
|
|
0,9
|
0,930
|
0,390
|
0,120
|
0,055
|
0,020
|
0,008
|
0,003
|
|
Таблица А.9
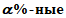 критические значения статистики Диксона (
D
5
N
)
критические значения статистики Диксона (
D
5
N
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,84
|
0,63
|
0,46
|
0,40
|
0,35
|
0,32
|
0,28
|
|
0,5
|
0,84
|
0,63
|
0,46
|
0,40
|
0,32
|
0,30
|
0,26
|
|
|
0,9
|
0,84
|
0,63
|
0,42
|
0,35
|
0,26
|
0,24
|
0,21
|
|
|
5
|
0
|
0,74
|
0,53
|
0,38
|
0,32
|
0,28
|
0,25
|
0,23
|
|
0,5
|
0,74
|
0,53
|
0,37
|
0,31
|
0,27
|
0,24
|
0,22
|
|
|
0,9
|
0,73
|
0,52
|
0,32
|
0,26
|
0,21
|
0,19
|
0,16
|
|
|
10
|
0
|
0,67
|
0,47
|
0,33
|
0,28
|
0,24
|
0,22
|
0,20
|
|
0,5
|
0,66
|
0,46
|
0,32
|
0,27
|
0,23
|
0,21
|
0,18
|
|
|
0,9
|
0,66
|
0,45
|
0,28
|
0,23
|
0,18
|
0,16
|
0,14
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,88
|
0,69
|
0,54
|
0,49
|
0,44
|
0,41
|
0,37
|
|
0,5
|
0,88
|
0,69
|
0,53
|
0,47
|
0,41
|
0,38
|
0,34
|
|
|
0,9
|
0,85
|
0,67
|
0,46
|
0,39
|
0,32
|
0,30
|
0,26
|
|
|
5
|
0
|
0,79
|
0,59
|
0,45
|
0,41
|
0,36
|
0,33
|
0,30
|
|
0,5
|
0,78
|
0,58
|
0,44
|
0,40
|
0,35
|
0,32
|
0,29
|
|
|
0,9
|
0,75
|
0,56
|
0,36
|
0,30
|
0,25
|
0,23
|
0,21
|
|
|
10
|
0
|
0,70
|
0,54
|
0,52
|
0,37
|
0,32
|
0,29
|
0,27
|
|
0,5
|
0,69
|
0,52
|
0,39
|
0,35
|
0,30
|
0,27
|
0,25
|
|
|
0,9
|
0,68
|
0,49
|
0,32
|
0,26
|
0,22
|
0,20
|
0,17
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,90
|
0,75
|
0,62
|
0,58
|
0,53
|
0,50
|
0,45
|
|
0,5
|
0,89
|
0,74
|
0,60
|
0,55
|
0,49
|
0,46
|
0,42
|
|
|
0,9
|
0,86
|
0,72
|
0,52
|
0,45
|
0,38
|
0,36
|
0,31
|
|
|
5
|
0
|
0,82
|
0,65
|
0,54
|
0,49
|
0,44
|
0,41
|
0,38
|
|
0,5
|
0,81
|
0,64
|
0,52
|
0,47
|
0,41
|
0,39
|
0,35
|
|
|
0,9
|
0,77
|
0,59
|
0,41
|
0,35
|
0,30
|
0,28
|
0,26
|
|
|
10
|
0
|
0,77
|
0,61
|
0,49
|
0,44
|
0,39
|
0,36
|
0,34
|
|
0,5
|
0,75
|
0,58
|
0,46
|
0,41
|
0,36
|
0,33
|
0,31
|
|
|
0,9
|
0,71
|
0,53
|
0,36
|
0,31
|
0,26
|
0,25
|
0,22
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,93
|
0,80
|
0,69
|
0,64
|
0,60
|
0,57
|
0,52
|
|
0,5
|
0,92
|
0,79
|
0,67
|
0,60
|
0,56
|
0,53
|
0,49
|
|
|
0,9
|
0,89
|
0,78
|
0,58
|
0,52
|
0,46
|
0,42
|
0,38
|
|
|
5
|
0
|
0,86
|
0,72
|
0,61
|
0,56
|
0,51
|
0,48
|
0,44
|
|
0,5
|
0,85
|
0,70
|
0,58
|
0,54
|
0,48
|
0,46
|
0,42
|
|
|
0,9
|
0,80
|
0,64
|
0,46
|
0,41
|
0,36
|
0,34
|
0,31
|
|
|
10
|
0
|
0,82
|
0,67
|
0,56
|
0,51
|
0,45
|
0,42
|
0,40
|
|
0,5
|
0,80
|
0,65
|
0,53
|
0,48
|
0,43
|
0,40
|
0,37
|
|
|
0,9
|
0,74
|
0,57
|
0,40
|
0,35
|
0,31
|
0,29
|
0,26
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,96
|
0,86
|
0,75
|
0,71
|
0,66
|
0,63
|
0,58
|
|
0,5
|
0,95
|
0,85
|
0,74
|
0,69
|
0,63
|
0,60
|
0,55
|
|
|
0,9
|
0,91
|
0,83
|
0,66
|
0,59
|
0,51
|
0,48
|
0,44
|
|
|
5
|
0
|
0,90
|
0,78
|
0,68
|
0,62
|
0,57
|
0,54
|
0,50
|
|
0,5
|
0,89
|
0,77
|
0,66
|
0,60
|
0,55
|
0,52
|
0,47
|
|
|
0,9
|
0,84
|
0,70
|
0,53
|
0,48
|
0,42
|
0,40
|
0,36
|
|
|
10
|
0
|
0,86
|
0,74
|
0,63
|
0,57
|
0,51
|
0,48
|
0,45
|
|
0,5
|
0,85
|
0,71
|
0,60
|
0,55
|
0,49
|
0,46
|
0,42
|
|
|
0,9
|
0,78
|
0,63
|
0,47
|
0,41
|
0,36
|
0,33
|
0,31
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,99
|
0,93
|
0,85
|
0,81
|
0,76
|
0,73
|
0,68
|
|
0,5
|
0,99
|
0,93
|
0,85
|
0,81
|
0,74
|
0,70
|
0,65
|
|
|
0,9
|
0,98
|
0,92
|
0,83
|
0,77
|
0,68
|
0,62
|
0,56
|
|
|
5
|
0
|
0,97
|
0,88
|
0,79
|
0,73
|
0,67
|
0,63
|
0,59
|
|
0,5
|
0,96
|
0,87
|
0,77
|
0,71
|
0,65
|
0,61
|
0,57
|
|
|
0,9
|
0,93
|
0,84
|
0,69
|
0,60
|
0,52
|
0,50
|
0,46
|
|
|
10
|
0
|
0,94
|
0,85
|
0,74
|
0,69
|
0,62
|
0,58
|
0,54
|
|
0,5
|
0,93
|
0,84
|
0,72
|
0,67
|
0,60
|
0,56
|
0,52
|
|
|
0,9
|
0,87
|
0,77
|
0,60
|
0,52
|
0,46
|
0,44
|
0,41
|
|
Таблица А.10
 критические значения статистики Диксона (
D
5
I
)
критические значения статистики Диксона (
D
5
I
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
0,84
|
0,63
|
0,46
|
0,10
|
0,32
|
0,28
|
0,24
|
|
0,5
|
0,84
|
0,63
|
0,45
|
0,38
|
0,31
|
0,27
|
0,24
|
|
|
0,9
|
0,84
|
0,63
|
0,43
|
0,35
|
0,28
|
0,24
|
0,23
|
|
|
5
|
0
|
0,74
|
0,53
|
0,37
|
0,32
|
0,26
|
0,23
|
0,20
|
|
0,5
|
0,74
|
0,53
|
0,37
|
0,30
|
0,25
|
0,22
|
0,19
|
|
|
0,9
|
0,74
|
0,51
|
0,34
|
0,26
|
0,20
|
0,18
|
0,16
|
|
|
10
|
0
|
0,67
|
0,47
|
0,33
|
0,28
|
0,23
|
0,20
|
0,18
|
|
0,5
|
0,67
|
0,47
|
0,32
|
0,27
|
0,22
|
0,19
|
0,17
|
|
|
0,9
|
0,67
|
0,45
|
0,29
|
0,23
|
0,18
|
0,16
|
0,14
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
0,89
|
0,55
|
0,38
|
0,31
|
0,22
|
0,19
|
0,17
|
|
0,5
|
0,83
|
0,58
|
0,38
|
0,31
|
0,22
|
0,19
|
0,17
|
|
|
0,9
|
0,83
|
0,6
|
0,39
|
0,31
|
0,22
|
0,19
|
0,17
|
|
|
5
|
0
|
0,68
|
0,45
|
0,30
|
0,23
|
0,13
|
0,16
|
0,14
|
|
0,5
|
0,72
|
0,45
|
0,30
|
0,23
|
0,18
|
0,16
|
0,14
|
|
|
0,9
|
0,73
|
0,45
|
0,29
|
0,22
|
0,16
|
0,14
|
0,12
|
|
|
10
|
0
|
0,62
|
0,40
|
0,26
|
0,21
|
0,16
|
0,14
|
0,12
|
|
0,5
|
0,64
|
0,40
|
0,25
|
0,20
|
0,15
|
0,13
|
0,11
|
|
|
0,9
|
0,66
|
0,40
|
0,25
|
0,18
|
0,14
|
0,12
|
0,10
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
0,76
|
0,49
|
0,28
|
0,22
|
0,14
|
0,11
|
0,10
|
|
0,5
|
0,82
|
0,52
|
0,29
|
0,23
|
0,15
|
0,12
|
0,10
|
|
|
0,9
|
0,82
|
0,57
|
0,35
|
0,25
|
0,17
|
0,15
|
0,12
|
|
|
5
|
0
|
0,64
|
0,39
|
0,22
|
0,16
|
0,12
|
0,09
|
0,08
|
|
0,5
|
0,68
|
0,41
|
0,23
|
0,16
|
0,12
|
0,09
|
0,08
|
|
|
0,9
|
0,71
|
0,45
|
0,26
|
0,18
|
0,13
|
0,10
|
0,08
|
|
|
10
|
0
|
0,57
|
0,33
|
0,19
|
0,14
|
0,10
|
0,08
|
0,07
|
|
0,5
|
0,60
|
0,35
|
0,19
|
0,14
|
0,10
|
0,08
|
0,07
|
|
|
0,9
|
0,64
|
0,38
|
0,22
|
0,15
|
0,10
|
0,08
|
0,07
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
0,72
|
0,43
|
0,20
|
0,14
|
0,08
|
0,06
|
0,04
|
|
0,5
|
0,80
|
0,46
|
0,22
|
0,15
|
0,09
|
0,07
|
0,05
|
|
|
0,9
|
0,80
|
0,55
|
0,31
|
0,20
|
0,12
|
0,10
|
0,03
|
|
|
5
|
0
|
0,59
|
0,31
|
0,14
|
0,10
|
0,06
|
0,04
|
0,03
|
|
0,5
|
0,64
|
0,35
|
0,16
|
0,11
|
0,06
|
0,05
|
0,03
|
|
|
0,9
|
0,69
|
0,42
|
0,21
|
0,14
|
0,08
|
0,06
|
0,05
|
|
|
10
|
0
|
0,50
|
0,26
|
0,12
|
0,08
|
0,05
|
0,04
|
0,03
|
|
0,5
|
0,55
|
0,29
|
0,13
|
0,09
|
0,05
|
0,04
|
0,03
|
|
|
0,9
|
0,62
|
0,35
|
0,18
|
0,11
|
0,07
|
0,05
|
0,04
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
0,68
|
0,36
|
0,13
|
0,07
|
0,04
|
0,02
|
0,015
|
|
0,5
|
0,76
|
0,40
|
0,15
|
0,09
|
0,04
|
0,03
|
0,03
|
|
|
0,9
|
0,79
|
0,51
|
0,27
|
0,17
|
0,08
|
0,06
|
0,05
|
|
|
5
|
0
|
0,54
|
0,24
|
0,09
|
0,050
|
0,025
|
0,015
|
0,01
|
|
0,5
|
0,54
|
0,29
|
0,11
|
0,060
|
0,030
|
0,020
|
0,01
|
|
|
0,9
|
0,66
|
0,33
|
0,17
|
0,100
|
0,060
|
0,040
|
0,03
|
|
|
10
|
0
|
0,44
|
0,19
|
0,07
|
0,040
|
0,020
|
0,010
|
0,008
|
|
0,5
|
0,44
|
0,23
|
0,08
|
0,045
|
0,020
|
0,015
|
0,009
|
|
|
0,9
|
0,58
|
0,31
|
0,14
|
0,085
|
0,045
|
0,030
|
0,020
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
0,58
|
0,22
|
0,04
|
0,01
|
0,004
|
0,002
|
0,001
|
|
0,5
|
0,69
|
0,29
|
0,07
|
0,025
|
0,006
|
0,004
|
0,001
|
|
|
0,9
|
0,75
|
0,44
|
0,20
|
0,10
|
0,045
|
0,020
|
0,015
|
|
|
5
|
0
|
0,41
|
0,12
|
0,02
|
0,008
|
0,002
|
0,001
|
0
|
|
0,5
|
0,48
|
0,18
|
0,035
|
0,010
|
0,004
|
0,001
|
0,001
|
|
|
0,9
|
0,60
|
0,31
|
0,110
|
0,055
|
0,020
|
0,010
|
0,005
|
|
|
10
|
0
|
0,32
|
0,09
|
0,015
|
0,005
|
0,001
|
0,001
|
0
|
|
0,5
|
0,40
|
0,13
|
0,025
|
0,007
|
0,002
|
0,001
|
0
|
|
|
0,9
|
0,52
|
0,23
|
0,090
|
0,040
|
0,010
|
0,006
|
0,003
|
|
Таблица А.11
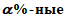 критические значения статистики
критические значения статистики
Смирнова-Граббса (
G
N
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
1,95
|
2,43
|
2,94
|
3,17
|
3,38
|
3,52
|
3,54
|
|
0,5
|
1,94
|
2,39
|
2,84
|
3,11
|
3,35
|
3,50
|
3,51
|
|
|
0,9
|
1,92
|
2,30
|
2,67
|
2,86
|
3,08
|
3,10
|
3,18
|
|
|
5
|
0
|
1,84
|
2,17
|
2,60
|
2,79
|
3,00
|
3,10
|
3,21
|
|
0,5
|
1,83
|
2,15
|
2,52
|
2,74
|
2,93
|
3,02
|
3,15
|
|
|
0,9
|
1,80
|
2,10
|
2,37
|
2,51
|
2,67
|
2,79
|
2,90
|
|
|
10
|
0
|
1,75
|
2,04
|
2,44
|
2,60
|
2,851
|
2,91
|
3,02
|
|
0,5
|
1,73
|
2,03
|
2,36
|
2,54
|
2,78
|
2,88
|
2,97
|
|
|
0,9
|
1,70
|
1,99
|
2,22
|
2,34
|
2,52
|
2,62
|
2,72
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
1,98
|
2,54
|
3,26
|
3,60
|
3,97
|
4,26
|
4,33
|
|
0,5
|
1,98
|
2,50
|
3,17
|
3,52
|
3,90
|
4,21
|
4,30
|
|
|
0,9
|
1,93
|
2,47
|
2,88
|
3,12
|
3,44
|
3,67
|
3,71
|
|
|
5
|
0
|
1,89
|
2,32
|
2,89
|
3,18
|
3,52
|
3,69
|
3,85
|
|
0,5
|
1,88
|
2,29
|
2,80
|
3,10
|
3,43
|
3,61
|
3,74
|
|
|
0,9
|
1,82
|
2,22
|
2,53
|
2,71
|
2,97
|
3,12
|
3,32
|
|
|
10
|
0
|
1,81
|
2,19
|
2,70
|
2,99
|
3,28
|
3,46
|
3,62
|
|
0,5
|
1,79
|
2,16
|
2,64
|
2,88
|
3,20
|
3,39
|
3,52
|
|
|
0,9
|
1,73
|
2,06
|
2,35
|
2,54
|
2,78
|
2,94
|
3,09
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
2,00
|
2,64
|
3,53
|
3,96
|
4,59
|
4,96
|
5,16
|
|
0,5
|
2,00
|
2,59
|
3,42
|
3,87
|
4,42
|
4,83
|
5,04
|
|
|
0,9
|
1,96
|
2,52
|
3,06
|
3,36
|
3,72
|
4,10
|
4,18
|
|
|
5
|
0
|
1,93
|
2,46
|
3,18
|
3,54
|
4,00
|
4,24
|
4,47
|
|
0,5
|
1,92
|
2,43
|
3,05
|
3,45
|
3,93
|
4,19
|
4,36
|
|
|
0,9
|
1,85
|
2,29
|
2,68
|
2,92
|
3,25
|
3,50
|
3,74
|
|
|
10
|
0
|
1,87
|
2,34
|
2,98
|
3,34
|
3,74
|
3,98
|
4,22
|
|
0,5
|
1,85
|
2,29
|
2,88
|
3,20
|
3,61
|
3,84
|
4,08
|
|
|
0,9
|
1,77
|
2,13
|
2,49
|
2,74
|
3,05
|
3,26
|
3,47
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
2,02
|
2,71
|
3,73
|
4,29
|
5,06
|
5,54
|
5,86
|
|
0,5
|
2,02
|
2,68
|
3,58
|
4,19
|
4,90
|
5,40
|
5,76
|
|
|
0,9
|
1,98
|
2,57
|
3,25
|
3,70
|
4,18
|
4,54
|
4,70
|
|
|
5
|
0
|
1,97
|
2,57
|
3,42
|
3,87
|
4,43
|
4,81
|
5,06
|
|
0,5
|
1,96
|
2,53
|
3,30
|
3,74
|
4,28
|
4,70
|
4,94
|
|
|
0,9
|
1,89
|
2,38
|
2,86
|
3,15
|
3,57
|
3,92
|
4,17
|
|
|
10
|
0
|
1,92
|
2,47
|
3,23
|
3,66
|
4,14
|
4,46
|
4,77
|
|
0,5
|
1,90
|
2,40
|
3,11
|
3,52
|
4,00
|
4,32
|
4,60
|
|
|
0,9
|
1,80
|
2,22
|
2,66
|
2,96
|
3,35
|
3,59
|
3,87
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
2,03
|
2,76
|
3,91
|
4,57
|
5,49
|
6,08
|
6,51
|
|
0,5
|
2,03
|
2,75
|
3,85
|
4,48
|
5,31
|
5,97
|
6,39
|
|
|
0,9
|
1,99
|
2,65
|
3,44
|
4,04
|
4,62
|
5,01
|
5,24
|
|
|
5
|
0
|
2,00
|
2,65
|
3,62
|
4,14
|
4,86
|
5,30
|
5,62
|
|
0,5
|
1,99
|
2,62
|
3,51
|
4,04
|
4,67
|
5,14
|
5,50
|
|
|
0,9
|
1,92
|
2,48
|
3,06
|
3,42
|
3,92
|
4,30
|
4,58
|
|
|
10
|
0
|
1,96
|
2,57
|
3,44
|
3,92
|
4,49
|
4,91
|
5,28
|
|
0,5
|
1,95
|
2,52
|
3,33
|
3,79
|
4,35
|
4,79
|
5,08
|
|
|
0,9
|
1,85
|
2,33
|
2,85
|
3,17
|
3,66
|
3,94
|
4,26
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
2,04
|
2,82
|
4,10
|
4,93
|
6,06
|
6,88
|
7,63
|
|
0,5
|
2,04
|
2,82
|
4,04
|
4,87
|
5,94
|
6,68
|
7,47
|
|
|
0,9
|
2,03
|
2,80
|
3,94
|
4,51
|
5,23
|
5,95
|
6,37
|
|
|
5
|
0
|
2,03
|
2,77
|
3,91
|
4,59
|
5,51
|
6,11
|
6,63
|
|
0,5
|
2,03
|
2,75
|
3,84
|
4,51
|
5,34
|
6,00
|
6,41
|
|
|
0,9
|
2,00
|
2,67
|
3,56
|
4,00
|
4,61
|
5,10
|
5,50
|
|
|
10
|
0
|
2,01
|
2,72
|
3,76
|
4,38
|
5,15
|
5,67
|
6,23
|
|
0,5
|
2,01
|
2,68
|
3,68
|
4,28
|
5,02
|
5,56
|
5,95
|
|
|
0,9
|
1,94
|
2,54
|
3,30
|
3,69
|
4,25
|
4,70
|
5,12
|
|
Таблица А.12
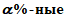 критические значения статистики
критические значения статистики
Смирнова-Граббса (
G
1
)
|
|
Коэффициент автокорреляции
r
(1)
|
Объем выборки (
n
)
|
||||||
|
6
|
10
|
20
|
30
|
50
|
70
|
100
|
||
|
C
s
= 0
|
||||||||
|
1
|
0
|
1,95
|
2,43
|
2,94
|
3,17
|
3,38
|
3,52
|
3,54
|
|
0,5
|
1,94
|
2,39
|
2,84
|
3,11
|
3,35
|
3,50
|
3,51
|
|
|
0,9
|
1,92
|
2,30
|
2,67
|
2,86
|
3,08
|
3,10
|
3,18
|
|
|
5
|
0
|
1,84
|
2,17
|
2,60
|
2,79
|
3,00
|
3,10
|
3,21
|
|
0,5
|
1,83
|
2,15
|
2,52
|
2,74
|
2,93
|
3,02
|
3,15
|
|
|
0,9
|
1,80
|
2,10
|
2,37
|
2,51
|
2,67
|
2,79
|
2,90
|
|
|
10
|
0
|
1,75
|
2,04
|
2,44
|
2,60
|
2,851
|
2,91
|
3,02
|
|
0,5
|
1,73
|
2,03
|
2,36
|
2,54
|
2,78
|
2,88
|
2,97
|
|
|
0,9
|
1,70
|
1,99
|
2,22
|
2,34
|
2,52
|
2,62
|
2,72
|
|
|
C
s
= 0,5
|
||||||||
|
1
|
0
|
1,88
|
2,27
|
2,50
|
2,51
|
2,53
|
2,55
|
2,57
|
|
0,5
|
1,90
|
2,28
|
2,53
|
2,60
|
2,63
|
2,64
|
2,65
|
|
|
0,9
|
1,93
|
2,29
|
2,56
|
2,64
|
2,72
|
2,74
|
2,86
|
|
|
5
|
0
|
1,74
|
2,00
|
2,22
|
2,28
|
2,36
|
2,39
|
2,42
|
|
0,5
|
1,76
|
2,02
|
2,24
|
2,30
|
2,38
|
2,41
|
2,44
|
|
|
0,9
|
1,78
|
2,04
|
2,26
|
2,32
|
2,40
|
2,44
|
2,48
|
|
|
10
|
0
|
1,66
|
1,88
|
2,09
|
2,17
|
2,27
|
2,29
|
2,32
|
|
0,5
|
1,65
|
1,87
|
2,07
|
2,16
|
2,26
|
2,28
|
2,31
|
|
|
0,9
|
1,64
|
1,86
|
2,06
|
2,15
|
2,25
|
2,27
|
2,30
|
|
|
C
s
= 1,0
|
||||||||
|
1
|
0
|
1,83
|
2,09
|
2,12
|
2,12
|
2,05
|
2,03
|
2,01
|
|
0,5
|
1,87
|
2,10
|
2,17
|
2,13
|
2,11
|
2,11
|
2,04
|
|
|
0,9
|
1,92
|
2,22
|
2,40
|
2,40
|
2,40
|
2,40
|
2,40
|
|
|
5
|
0
|
1,66
|
1,80
|
1,91
|
1,91
|
1,91
|
1,91
|
1,91
|
|
0,5
|
1,70
|
1,86
|
1,93
|
1,93
|
1,93
|
1,93
|
1,93
|
|
|
0,9
|
1,74
|
1,94
|
2,09
|
2,09
|
2,10
|
2,10
|
2,13
|
|
|
10
|
0
|
1,56
|
1,70
|
1,78
|
1,80
|
1,83
|
1,83
|
1,83
|
|
0,5
|
1,60
|
1,72
|
1,82
|
1,83
|
1,85
|
1,85
|
1,85
|
|
|
0,9
|
1,65
|
1,81
|
1,95
|
1,95
|
1,96
|
1,98
|
1,99
|
|
|
C
s
= 1,5
|
||||||||
|
1
|
0
|
1,78
|
1,91
|
1,82
|
1,73
|
1,66
|
1,60
|
1,56
|
|
0,5
|
1,83
|
1,93
|
1,87
|
1,81
|
1,70
|
1,66
|
1,61
|
|
|
0,9
|
1,89
|
2,11
|
2,26
|
2,22
|
2,10
|
2,01
|
2,00
|
|
|
5
|
0
|
1,56
|
1,61
|
1,60
|
1,57
|
1,53
|
1,50
|
1,48
|
|
0,5
|
1,62
|
1,69
|
1,68
|
1,62
|
1,58
|
1,54
|
1,51
|
|
|
0,9
|
1,71
|
1,86
|
1,94
|
1,87
|
1,84
|
1,81
|
1,79
|
|
|
10
|
0
|
1,45
|
1,51
|
1,50
|
1,48
|
1,46
|
1,44
|
1,44
|
|
0,5
|
1,52
|
1,57
|
1,56
|
1,53
|
1,51
|
1,48
|
1,47
|
|
|
0,9
|
1,60
|
1,72
|
1,79
|
1,75
|
1,71
|
1,70
|
1,69
|
|
|
C
s
= 2,0
|
||||||||
|
1
|
0
|
1,70
|
1,71
|
1,53
|
1,44
|
1,35
|
1,28
|
1,24
|
|
0,5
|
1,78
|
1,77
|
1,62
|
1,53
|
1,43
|
1,35
|
1,31
|
|
|
0,9
|
1,88
|
2,04
|
2,10
|
1,97
|
1,84
|
1,73
|
1,71
|
|
|
5
|
0
|
1,46
|
1,46
|
1,35
|
1,30
|
1,25
|
1,20
|
1,17
|
|
0,5
|
1,54
|
1,54
|
1,44
|
1,36
|
1,29
|
1,25
|
1,22
|
|
|
0,9
|
1,66
|
1,79
|
1,78
|
1,69
|
1,61
|
1,56
|
1,52
|
|
|
10
|
0
|
1,34
|
1,34
|
1,27
|
1,23
|
1,18
|
1,15
|
1,15
|
|
0,5
|
1,43
|
1,43
|
1,35
|
1,29
|
1,23
|
1,20
|
1,17
|
|
|
0,9
|
1,55
|
1,63
|
1,63
|
1,59
|
1,50
|
1,46
|
1,43
|
|
|
C
s
= 3,0
|
||||||||
|
1
|
0
|
1,53
|
1,38
|
1,12
|
1,04
|
0,97
|
0,92
|
0,87
|
|
0,5
|
1,65
|
1,52
|
1,28
|
1,15
|
1,04
|
0,96
|
0,92
|
|
|
0,9
|
1,83
|
1,87
|
1,84
|
1,64
|
1,46
|
1,35
|
1,31
|
|
|
5
|
0
|
1,26
|
1,17
|
1,02
|
0,94
|
0,89
|
0,85
|
0,82
|
|
0,5
|
1,38
|
1,28
|
1,10
|
1,03
|
0,94
|
0,89
|
0,85
|
|
|
0,9
|
1,76
|
1,63
|
1,52
|
1,41
|
1,28
|
1,21
|
1,12
|
|
|
10
|
0
|
1,15
|
1,08
|
0,95
|
0,89
|
0,84
|
0,81
|
0,80
|
|
0,5
|
1,25
|
1,18
|
1,02
|
0,95
|
0,88
|
0,85
|
0,82
|
|
|
0,9
|
1,50
|
1,46
|
1,38
|
1,30
|
1,17
|
1,10
|
1,04
|
|
Таблица А.13
Критические значения статистики Фишера (
F*
) в зависимости
от уровня значимости
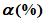 , коэффициентов внутрирядной
, коэффициентов внутрирядной
(
r
(1)) и межрядной корреляции (
R
) при равных объемах
двух выборок (
n
x
=
n
y
)
|
R
|
r
(1)
|
|
||||||||||||
|
0,1
|
0,5
|
1
|
2,5
|
5
|
10
|
15
|
25
|
35
|
40
|
45
|
47,5
|
50
|
||
|
n
x
=
n
y
= 10
|
||||||||||||||
|
0,0
|
0,7
|
18,6
|
11,0
|
8,11
|
6,19
|
4,58
|
3,22
|
2,59
|
1,83
|
1,41
|
1,26
|
1,12
|
1,06
|
1,00
|
|
0,6
|
14,4
|
9,51
|
7,54
|
5,63
|
4,20
|
2,98
|
2,42
|
1,77
|
1,38
|
1,25
|
1,12
|
1,06
|
1,00
|
|
|
0,5
|
12,6
|
8,58
|
6,97
|
5,16
|
3,89
|
2,79
|
2,29
|
1,71
|
1,36
|
1,24
|
1,11
|
1,06
|
1,00
|
|
|
0,4
|
11,7
|
7,92
|
6,42
|
4,79
|
3,68
|
2,66
|
2,20
|
1,67
|
1,34
|
1,23
|
1,10
|
1,06
|
1,00
|
|
|
0,3
|
11,1
|
7,42
|
6,08
|
4,52
|
3,51
|
2,57
|
2,15
|
1,63
|
1,33
|
1,22
|
1,10
|
1,05
|
1,00
|
|
|
0,2
|
10,5
|
7,07
|
5,77
|
4,32
|
3,34
|
2,51
|
2,08
|
1,60
|
1,31
|
1,21
|
1,10
|
1,04
|
1,00
|
|
|
0,1
|
10,2
|
6,78
|
5,51
|
4,16
|
3,24
|
2,46
|
2,04
|
1,58
|
1,30
|
1,20
|
1,10
|
1,04
|
1,00
|
|
|
0,0
|
10,1
|
6,54
|
5,35
|
4,03
|
3,18
|
2,44
|
2,02
|
1,57
|
1,30
|
1,19
|
1,10
|
1,03
|
1,00
|
|
|
0,95
|
0,0
|
2,47
|
2,01
|
1,84
|
1,63
|
1,48
|
1,33
|
1,25
|
1,15
|
1,09
|
1,03
|
1,00
|
1,00
|
1,00
|
|
0,9
|
3,47
|
2,67
|
2,32
|
1,98
|
1,70
|
1,48
|
1,37
|
1,22
|
1,13
|
1,07
|
1,02
|
1,00
|
1,00
|
|
|
0,8
|
4,89
|
3,60
|
3,11
|
2,49
|
2,10
|
1,73
|
1,56
|
1,32
|
1,18
|
1,12
|
1,05
|
1,00
|
1,00
|
|
|
0,7
|
6,21
|
4,41
|
8,76
|
2,93
|
2,42
|
1,92
|
1,69
|
1,39
|
1,22
|
1,15
|
1,08
|
1,00
|
1,00
|
|
|
0,6
|
7,28
|
5,08
|
4,32
|
3,30
|
2,69
|
2,07
|
1,79
|
1,45
|
1,25
|
1,17
|
1,08
|
1,01
|
1,00
|
|
|
0,5
|
8,20
|
5,62
|
4,73
|
3,58
|
2,88
|
2,20
|
1,86
|
1,49
|
1,27
|
1,18
|
1,09
|
1,01
|
1,00
|
|
|
0,4
|
8,97
|
6,06
|
5,03
|
3,80
|
3,02
|
2,28
|
1,93
|
1,52
|
1,28
|
1,18
|
1,09
|
1,02
|
1,00
|
|
|
0,3
|
9,51
|
8,32
|
5,24
|
3,94
|
3,12
|
2,37
|
1,99
|
1,55
|
1,29
|
1,18
|
1,10
|
1,02
|
1,00
|
|
|
0,2
|
10,0
|
6,54
|
5,35
|
4,03
|
3,18
|
2,44
|
2,02
|
1,57
|
1,30
|
1,19
|
1,10
|
1,03
|
1,00
|
|
|
n
x
=
n
y
= 25
|
||||||||||||||
|
0,0
|
0,7
|
7,17
|
5,18
|
4,39
|
3,44
|
2,86
|
2,22
|
1,92
|
1,70
|
1,88
|
1,20
|
1,06
|
1,02
|
1,00
|
|
0,6
|
5,82
|
4,42
|
3,80
|
3,00
|
2,53
|
2,04
|
1,79
|
1,52
|
1,24
|
1,18
|
1,06
|
1,02
|
1,00
|
|
|
0,5
|
4,99
|
3,85
|
3,39
|
2,73
|
2,31
|
1,90
|
1,69
|
1,42
|
1,22
|
1,16
|
1,05
|
1,02
|
1,00
|
|
|
0,4
|
4,55
|
3,54
|
3,11
|
2,53
|
2,16
|
1,80
|
1,60
|
1,36
|
1,19
|
1,14
|
1,05
|
1,02
|
1,00
|
|
|
0,3
|
4,24
|
3,28
|
2,90
|
2,40
|
2,08
|
1,75
|
1,55
|
1,34
|
1,17
|
1,12
|
1,05
|
1,02
|
1,00
|
|
|
0,2
|
4,04
|
3,12
|
2,76
|
2,34
|
2,03
|
1,72
|
1,54
|
1,33
|
1,17
|
1,12
|
1,05
|
1,02
|
1,00
|
|
|
0,1
|
3,88
|
3,02
|
2,68
|
2,29
|
2,00
|
1,71
|
1,53
|
1,32
|
1,17
|
1,11
|
1,05
|
1,02
|
1,00
|
|
|
0,0
|
3,74
|
2,97
|
2,66
|
2,27
|
1,98
|
1,70
|
1,53
|
1,32
|
1,17
|
1,11
|
1,05
|
1,02
|
1,00
|
|
|
0,2
|
0,0
|
3,42
|
2,84
|
2,60
|
2,22
|
1,95
|
1,67
|
1,52
|
1,32
|
1,17
|
1,10
|
1,05
|
1,02
|
1,00
|
|
0,3
|
3,33
|
2,78
|
2,54
|
2,18
|
1,92
|
1,64
|
1,50
|
1,30
|
1,16
|
1,10
|
1,05
|
1,02
|
1,00
|
|
|
0,4
|
3,22
|
2,70
|
2,46
|
2,12
|
1,87
|
1,61
|
1,47
|
1,28
|
1,15
|
1,10
|
1,05
|
1,02
|
1,00
|
|
|
0,5
|
3,07
|
2,58
|
2,34
|
2,04
|
1,80
|
1,57
|
1,43
|
1,26
|
1,14
|
1,09
|
1,04
|
1,02
|
1,00
|
|
|
0,6
|
2,87
|
2,44
|
2,21
|
1,93
|
1,72
|
1,51
|
1,39
|
1,24
|
1,13
|
1,08
|
1,04
|
1,02
|
1,00
|
|
|
0,7
|
2,61
|
2,23
|
2,03
|
1,80
|
1,63
|
1,44
|
1,33
|
1,22
|
1,11
|
1,06
|
1,03
|
1,02
|
1,00
|
|
|
0,8
|
2,28
|
1,95
|
1,82
|
1,63
|
1,49
|
1,36
|
1,27
|
1,17
|
1,09
|
1,05
|
1,03
|
1,02
|
1,00
|
|
|
0,9
|
1,83
|
1,61
|
1,55
|
1,42
|
1,33
|
1,25
|
1,18
|
1,12
|
1,06
|
1,03
|
1,02
|
1,01
|
1,00
|
|
|
0,95
|
1,54
|
1,41
|
1,37
|
1,29
|
1,22
|
1,18
|
1,13
|
1,09
|
1,05
|
1,02
|
1,01
|
1,00
|
1,00
|
|
|
n
x
=
n
y
= 50
|
||||||||||||||
|
0,0
|
0,7
|
4,07
|
3,31
|
2,98
|
2,49
|
2,16
|
1,82
|
1,64
|
1,40
|
1,22
|
1,15
|
1,07
|
1,02
|
1,00
|
|
0,6
|
2,52
|
2,90
|
2,65
|
2,26
|
1,97
|
1,69
|
1,55
|
1,34
|
1,18
|
1,13
|
1,06
|
1,02
|
1,00
|
|
|
0,5
|
3,15
|
2,62
|
2,40
|
2,08
|
1,82
|
1,58
|
1,48
|
1,30
|
1,15
|
1,11
|
1,05
|
1,01
|
1,00
|
|
|
0,4
|
2,88
|
2,42
|
2,23
|
1,94
|
1,72
|
1,51
|
1,42
|
1,25
|
1,13
|
1,10
|
1,04
|
1,01
|
1,00
|
|
|
0,3
|
2,68
|
2,27
|
2,10
|
1,83
|
1,65
|
1,48
|
1,38
|
1,22
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,2
|
2,58
|
2,19
|
2,02
|
1,79
|
1,63
|
1,47
|
1,37
|
1,21
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,1
|
2,52
|
2,15
|
1,99
|
1,79
|
1,62
|
1,47
|
1,37
|
1,21
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,0
|
2,51
|
2,15
|
1,99
|
1,79
|
1,62
|
1,47
|
1,37
|
1,21
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,2
|
0,0
|
2,51
|
2,15
|
1,99
|
1,79
|
1,62
|
1,47
|
1,37
|
1,21
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
0,3
|
2,46
|
2,10
|
1,94
|
1,76
|
1,60
|
1,46
|
1,36
|
1,21
|
1,12
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,4
|
2,39
|
2,05
|
1,88
|
1,72
|
1,57
|
1,44
|
1,34
|
1,20
|
1,11
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,5
|
2,3
|
1,96
|
1,81
|
1,67
|
1,53
|
1,41
|
1,32
|
1,19
|
1,11
|
1,09
|
1,04
|
1,01
|
1,00
|
|
|
0,6
|
2,17
|
1,85
|
1,73
|
1,60
|
1,48
|
1,36
|
1,30
|
1,18
|
1,10
|
1,08
|
1,04
|
1,00
|
1,00
|
|
|
0,7
|
2,01
|
1,72
|
1,63
|
1,52
|
1,42
|
1,32
|
1,26
|
1,16
|
1,08
|
1,06
|
1,02
|
1,00
|
1,00
|
|
|
0,8
|
1,80
|
1,58
|
1,52
|
1,42
|
1,33
|
1,25
|
1,2
|
1,13
|
1,06
|
1,04
|
1,01
|
1,00
|
1,00
|
|
|
0,9
|
1,54
|
1,39
|
1,35
|
1,28
|
1,23
|
1,18
|
1,14
|
1,09
|
1,05
|
1,03
|
1,00
|
1,00
|
1,00
|
|
|
0,95
|
1,32
|
1,27
|
1,24
|
1,20
|
1,16
|
1,13
|
1,10
|
1,07
|
1,04
|
1,03
|
1,00
|
1,00
|
1,00
|
|
|
n
x
=
n
y
= 100
|
||||||||||||||
|
0,0
|
0,7
|
3,02
|
2,49
|
2,28
|
1,93
|
1,72
|
1,52
|
1,40
|
1,24
|
1,13
|
1,10
|
1,03
|
1,00
|
1,00
|
|
0,6
|
2,66
|
2,20
|
2,03
|
1,76
|
1,59
|
1,44
|
1,36
|
1,23
|
1,12
|
1,09
|
1,02
|
1,00
|
1,00
|
|
|
0,5
|
2,40
|
2,00
|
1,85
|
1,64
|
1,51
|
1,39
|
1,31
|
1,21
|
1,11
|
1,09
|
1,02
|
1,00
|
1,00
|
|
|
0,4
|
2,20
|
1,87
|
1,76
|
1,56
|
1,46
|
1,36
|
1,28
|
1,19
|
1,10
|
1,08
|
1,02
|
1,00
|
1,00
|
|
|
0,3
|
2,06
|
1,80
|
1,70
|
1,53
|
1,42
|
1,34
|
1,26
|
1,18
|
1,10
|
1,07
|
1,02
|
1,00
|
1,00
|
|
|
0,2
|
1,98
|
1,76
|
1,67
|
1,52
|
1,41
|
1,33
|
1,25
|
1,17
|
1,10
|
1,06
|
1,02
|
1,00
|
1,00
|
|
|
0,1
|
1,94
|
1,74
|
1,65
|
1,52
|
1,41
|
1,32
|
1,24
|
1,16
|
1,09
|
1,06
|
1,02
|
1,00
|
1,00
|
|
|
0,0
|
1,91
|
1,73
|
1,64
|
1,51
|
1,41
|
1,31
|
1,22
|
1,16
|
1,08
|
1,05
|
1,02
|
1,00
|
1,00
|
|
|
0,2
|
0,0
|
1,81
|
1,70
|
1,61
|
1,50
|
1,40
|
1,30
|
1,21
|
1,15
|
1,07
|
1,04
|
1,02
|
1,00
|
1,00
|
|
0,3
|
1,76
|
1,67
|
1,59
|
1,47
|
1,38
|
1,30
|
1,20
|
1,15
|
1,06
|
1,04
|
1,02
|
1,00
|
1,00
|
|
|
0,4
|
1,72
|
1,63
|
1,56
|
1,45
|
1,36
|
1,28
|
1,19
|
1,14
|
1,06
|
1,03
|
1,02
|
1,00
|
1,00
|
|
|
0,5
|
1,66
|
1,58
|
1,52
|
1,42
|
1,34
|
1,26
|
1,18
|
1,12
|
1,05
|
1,03
|
1,02
|
1,00
|
1,00
|
|
|
0,6
|
1,60
|
1,52
|
1,47
|
1,38
|
1,32
|
1,24
|
1,17
|
1,11
|
1,05
|
1,02
|
1,02
|
1,00
|
1,00
|
|
|
0,7
|
1,53
|
1,46
|
1,40
|
1,32
|
1,27
|
1,22
|
1,15
|
1,10
|
1,04
|
1,02
|
1,01
|
1,00
|
1,00
|
|
|
0,8
|
1,43
|
1,37
|
1,32
|
1,26
|
1,21
|
1,17
|
1,13
|
1,08
|
1,03
|
1,02
|
1,01
|
1,00
|
1,00
|
|
|
0,9
|
1,29
|
1,24
|
1,22
|
1,17
|
1,14
|
1,11
|
1,09
|
1,05
|
1,02
|
1,02
|
1,01
|
1,00
|
1,00
|
|
|
0,95
|
1,20
|
1,18
|
1,17
|
1,12
|
1,10
|
1,08
|
1,06
|
1,03
|
1,02
|
1,01
|
1,00
|
1,00
|
1,00
|
|
Таблица А.14
Зависимость коэффициента
g
от
C
s
при определении
новых степеней свободы для критерия Фишера
|
C
s
|
0
|
0,5
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
4,0
|
|
g
|
1,0
|
0,82
|
0,62
|
0,45
|
0,30
|
0,24
|
0,17
|
0,14
|
0,10
|
Таблица А.15
Критические значения статистики Стьюдента (
t*
) в зависимости
от уровня значимости
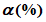 , коэффициентов внутрирядной
, коэффициентов внутрирядной
(
r
(1)) и межрядной корреляции (
R
) при равных объемах
двух выборок (
n
x
=
n
y
)
|
R
|
r
(1)
|
|
|||||||||||||
|
0,05
|
0,1
|
0,5
|
1
|
2,5
|
5
|
10
|
15
|
20
|
35
|
40
|
45
|
47,5
|
49,5
|
||
|
n
x
=
n
y
= 10;
k
=
n
x
+
n
y
- 2 = 18
|
|||||||||||||||
|
0,0
|
0,7
|
10,0
|
9,14
|
7,19
|
6,35
|
5,18
|
4,21
|
3,22
|
2,63
|
1,66
|
0,93
|
0,62
|
0,81
|
0,13
|
0,03
|
|
0,6
|
8,25
|
7,57
|
5,74
|
5,25
|
4,31
|
3,51
|
2,73
|
2,18
|
1,38
|
0,79
|
0,52
|
0,26
|
0,12
|
0,02
|
|
|
0,5
|
6,80
|
6,24
|
4,91
|
4,34
|
3,56
|
2,93
|
2,24
|
1,82
|
1,17
|
0,68
|
0,45
|
0,21
|
0,10
|
0,00
|
|
|
0,4
|
5,93
|
5,43
|
4,24
|
3,79
|
3,10
|
2,58
|
1,95
|
1,59
|
1,02
|
0,58
|
0,39
|
0,19
|
0,09
|
0,00
|
|
|
0,3
|
5,18
|
4,78
|
3,77
|
3,33
|
2,75
|
2,27
|
1,72
|
1,40
|
0,91
|
0,51
|
0,35
|
0,18
|
0,08
|
0,00
|
|
|
0,2
|
4,65
|
4,33
|
3,38
|
3,02
|
2,47
|
2,07
|
1,56
|
1,26
|
0,82
|
0,47
|
0,32
|
0,16
|
0,05
|
0,00
|
|
|
0,1
|
4,23
|
3,94
|
3,07
|
2,76
|
2,26
|
1,90
|
1,43
|
1,16
|
0,75
|
0,43
|
0,29
|
0,14
|
0,03
|
0,00
|
|
|
0,0
|
3,92
|
3,61
|
2,88
|
2,55
|
2,10
|
1,73
|
1,33
|
1,07
|
0,69
|
0,39
|
0,26
|
0,12
|
0,02
|
0,00
|
|
|
0,1
|
0,0
|
3,63
|
3,34
|
2,68
|
2,37
|
1,94
|
1,60
|
1,22
|
0,99
|
0,63
|
0,36
|
0,23
|
0,11
|
0,01
|
0,00
|
|
0,2
|
3,35
|
3,09
|
2,48
|
2,19
|
1,80
|
1,48
|
1,12
|
0,91
|
0,58
|
0,33
|
0,21
|
0,10
|
0,00
|
0,00
|
|
|
0,3
|
3,11
|
2,84
|
2,29
|
2,04
|
1,68
|
1,38
|
1,05
|
0,85
|
0,54
|
0,30
|
0,20
|
0,09
|
0,00
|
0,00
|
|
|
0,4
|
2,87
|
2,60
|
2,11
|
1,88
|
1,55
|
1,29
|
0,97
|
0,79
|
0,50
|
0,28
|
0,19
|
0,09
|
0,00
|
0,00
|
|
|
0,5
|
2,64
|
2,38
|
1,91
|
1,72
|
1,42
|
1,20
|
0,89
|
0,72
|
0,46
|
0,25
|
0,18
|
0,08
|
0,00
|
0,00
|
|
|
0,6
|
2,40
|
2,16
|
1,72
|
1,56
|
1,28
|
1,10
|
0,81
|
0,65
|
0,43
|
0,22
|
0,16
|
0,08
|
0,00
|
0,00
|
|
|
0,7
|
2,13
|
1,96
|
1,53
|
1,36
|
1,12
|
0,97
|
0,72
|
0,56
|
0,38
|
0,19
|
0,14
|
0,07
|
0,00
|
0,00
|
|
|
0,8
|
1,86
|
1,70
|
1,31
|
1,14
|
0,92
|
0,82
|
0,58
|
0,45
|
0,30
|
0,15
|
0,11
|
0,06
|
0,00
|
0,00
|
|
|
0,9
|
1,34
|
1,26
|
0,98
|
0,82
|
0,66
|
0,59
|
0,41
|
0,31
|
0,20
|
0,10
|
0,08
|
0,04
|
0,00
|
0,00
|
|
|
0,95
|
1,02
|
0,93
|
0,69
|
0,58
|
0,48
|
0,39
|
0,29
|
0,22
|
0,14
|
0,08
|
0,05
|
0,03
|
0,00
|
0,00
|
|
|
n
x
=
n
y
= 25;
k
=
n
x
+
n
y
- 2 = 48
|
|||||||||||||||
|
0,0
|
0,7
|
9,08
|
8,40
|
6,71
|
6,00
|
4,96
|
4,12
|
3,12
|
2,53
|
1,60
|
0,93
|
0,62
|
0,31
|
0,13
|
0,03
|
|
0,6
|
7,48
|
6,90
|
5,55
|
4,90
|
4,15
|
3,38
|
2,64
|
2,06
|
1,37
|
0,79
|
0,52
|
0,26
|
0,11
|
0,02
|
|
|
0,5
|
6,21
|
5,84
|
4,66
|
4,18
|
3,47
|
2,88
|
2,20
|
1,78
|
1,17
|
0,68
|
0,45
|
0,21
|
0,10
|
0,00
|
|
|
0,4
|
5,46
|
5,08
|
4,10
|
3,70
|
3,01
|
2,53
|
1,91
|
1,53
|
1,01
|
0,58
|
0,39
|
0,19
|
0,09
|
0,00
|
|
|
0,3
|
4,80
|
4,48
|
3,67
|
3,28
|
2,68
|
2,23
|
1,69
|
1,40
|
0,91
|
0,51
|
0,35
|
0,17
|
0,08
|
0,00
|
|
|
0,2
|
4,28
|
4,01
|
3,27
|
2,89
|
2,42
|
2,03
|
1,53
|
1,27
|
0,81
|
0,47
|
0,31
|
0,15
|
0,06
|
0,00
|
|
|
0,1
|
3,89
|
3,61
|
2,96
|
2,63
|
2,20
|
1,84
|
1,40
|
1,16
|
0,74
|
0,44
|
0,28
|
0,13
|
0,04
|
0,00
|
|
|
0,0
|
3,51
|
3,27
|
2,68
|
2,41
|
2,01
|
1,68
|
1,30
|
1,06
|
0,68
|
0,40
|
0,25
|
0,12
|
0,03
|
0,00
|
|
|
0,1
|
0,0
|
3,30
|
3,08
|
2,54
|
2,25
|
1,94
|
1,58
|
1,22
|
0,98
|
0,64
|
0,37
|
0,23
|
0,11
|
0,02
|
0,00
|
|
0,2
|
3,09
|
2,88
|
2,38
|
2,11
|
1,80
|
1,49
|
1,13
|
0,92
|
0,59
|
0,34
|
0,22
|
0,10
|
0,01
|
0,00
|
|
|
0,3
|
2,87
|
2,70
|
2,22
|
1,97
|
1,67
|
1,39
|
1,06
|
0,86
|
0,59
|
0,32
|
0,20
|
0,09
|
0,00
|
0,00
|
|
|
0,4
|
2,66
|
2,49
|
2,06
|
1,83
|
1,53
|
1,29
|
0,98
|
0,80
|
0,52
|
0,29
|
0,19
|
0,09
|
0,00
|
0,00
|
|
|
0,5
|
2,43
|
2,27
|
1,87
|
1,68
|
1,42
|
1,18
|
0,91
|
0,74
|
0,49
|
0,28
|
0,18
|
0,08
|
0,00
|
0,00
|
|
|
0,6
|
2,18
|
2,04
|
1,68
|
1,52
|
1,28
|
1,06
|
0,83
|
0,67
|
0,44
|
0,25
|
0,17
|
0,07
|
0,00
|
0,00
|
|
|
0,7
|
1,92
|
1,80
|
1,47
|
1,33
|
1,12
|
0,92
|
0,72
|
0,58
|
0,38
|
0,22
|
0,15
|
0,06
|
0,00
|
0,00
|
|
|
0,8
|
1,64
|
1,52
|
1,22
|
1,10
|
0,91
|
0,74
|
0,59
|
0,47
|
0,31
|
0,18
|
0,12
|
0,05
|
0,00
|
0,00
|
|
|
0,9
|
1,24
|
1,14
|
0,88
|
0,77
|
0,64
|
0,52
|
0,42
|
0,32
|
0,21
|
0,12
|
0,08
|
0,03
|
0,00
|
0,00
|
|
|
0,95
|
0,88
|
0,80
|
0,62
|
0,55
|
0,44
|
0,37
|
0,29
|
0,23
|
0,15
|
0,08
|
0,05
|
0,02
|
0,00
|
0,00
|
|
|
n
x
=
n
y
= 50;
k
=
n
x
+
n
y
- 2 = 98
|
|||||||||||||||
|
0,0
|
0,7
|
7,96
|
7,48
|
6,22
|
5,68
|
4,78
|
4,01
|
3,11
|
2,53
|
1,60
|
0,93
|
0,62
|
0,31
|
0,13
|
0,03
|
|
0,6
|
6,88
|
6,40
|
5,27
|
4,78
|
4,00
|
3,31
|
2,62
|
2,06
|
1,37
|
0,78
|
0,52
|
0,26
|
0,11
|
0,01
|
|
|
0,5
|
5,90
|
5,51
|
4,52
|
4,07
|
3,36
|
2,82
|
2,19
|
1,78
|
1,17
|
0,68
|
0,45
|
0,21
|
0,10
|
0,00
|
|
|
0,4
|
5,17
|
4,84
|
3,98
|
3,55
|
2,92
|
2,46
|
1,91
|
1,53
|
1,01
|
0,59
|
0,38
|
0,18
|
0,09
|
0,00
|
|
|
0,3
|
4,60
|
4,35
|
3,50
|
3,10
|
2,59
|
2,18
|
1,69
|
1,39
|
0,91
|
0,51
|
0,34
|
0,16
|
0,08
|
0,00
|
|
|
0,2
|
4,10
|
3,86
|
3,17
|
2,79
|
2,36
|
1,98
|
1,53
|
1,24
|
0,81
|
0,48
|
0,31
|
0,15
|
0,06
|
0,00
|
|
|
0,1
|
3,72
|
3,48
|
2,88
|
2,55
|
2,16
|
1,81
|
1,40
|
1,13
|
0,74
|
0,44
|
0,29
|
0,14
|
0,05
|
0,00
|
|
|
0,0
|
3,39
|
3,18
|
2,63
|
2,37
|
1,99
|
1,66
|
1,29
|
1,04
|
0,68
|
0,40
|
0,26
|
0,13
|
0,04
|
0,00
|
|
|
0,1
|
0,0
|
3,06
|
2,86
|
2,39
|
2,21
|
2,21
|
1,84
|
1,57
|
0,96
|
0,63
|
0,38
|
0,24
|
0,12
|
0,02
|
0,00
|
|
0,2
|
2,80
|
2,62
|
2,20
|
2,08
|
1,72
|
1,46
|
1,12
|
0,90
|
0,59
|
0,35
|
0,23
|
0,11
|
0,01
|
0,00
|
|
|
0,3
|
2,60
|
2,45
|
2,07
|
1,94
|
1,60
|
1,37
|
1,05
|
0,85
|
0,56
|
0,32
|
0,22
|
0,10
|
0,00
|
0,00
|
|
|
0,4
|
2,44
|
2,29
|
1,92
|
1,81
|
1,49
|
1,28
|
0,98
|
0,79
|
0,52
|
0,30
|
0,21
|
0,09
|
0,00
|
0,00
|
|
|
0,5
|
2,24
|
2,13
|
1,78
|
1,65
|
1,36
|
1,19
|
0,90
|
0,74
|
0,48
|
0,29
|
0,20
|
0,08
|
0,00
|
0,00
|
|
|
0,6
|
2,05
|
1,95
|
1,62
|
1,47
|
1,23
|
1,03
|
0,81
|
0,66
|
0,44
|
0,27
|
0,18
|
0,07
|
0,00
|
0,00
|
|
|
0,7
|
1,83
|
1,74
|
1,42
|
1,27
|
1,07
|
0,89
|
0,69
|
0,56
|
0,38
|
0,23
|
0,15
|
0,06
|
0,00
|
0,00
|
|
|
0,8
|
1,58
|
1,49
|
1,19
|
1,04
|
0,88
|
0,72
|
0,56
|
0,45
|
0,30
|
0,18
|
0,12
|
0,05
|
0,00
|
0,00
|
|
|
0,9
|
1,17
|
1,09
|
0,84
|
0,74
|
0,64
|
0,53
|
0,40
|
0,30
|
0,26
|
0,13
|
0,08
|
0,03
|
0,00
|
0,00
|
|
|
0,95
|
0,81
|
0,77
|
0,59
|
0,52
|
0,44
|
0,37
|
0,29
|
0,22
|
0,14
|
0,08
|
0,05
|
0,02
|
0,00
|
0,00
|
|
|
n
x
=
n
y
= 100;
k
=
n
x
+
n
y
- 2 = 198
|
|||||||||||||||
|
0,0
|
0,7
|
7,84
|
7,35
|
6,10
|
5,52
|
4,65
|
3,93
|
3,07
|
2,52
|
1,60
|
0,93
|
0,62
|
0,31
|
0,10
|
0,03
|
|
0,6
|
6,74
|
6,27
|
5,21
|
4,71
|
3,99
|
3,26
|
2,60
|
2,05
|
1,37
|
0,79
|
0,53
|
0,25
|
0,10
|
0,02
|
|
|
0,5
|
5,80
|
5,47
|
4,52
|
4,07
|
3,36
|
2,82
|
2,19
|
1,78
|
1,17
|
0,68
|
0,45
|
0,21
|
0,10
|
0,00
|
|
|
0,4
|
5,08
|
4,76
|
3,98
|
3,55
|
2,92
|
2,46
|
1,91
|
1,51
|
1,01
|
0,58
|
0,39
|
0,19
|
0,08
|
0,00
|
|
|
0,3
|
4,52
|
4,23
|
3,50
|
3,10
|
2,59
|
2,18
|
1,69
|
1,38
|
0,91
|
0,51
|
0,34
|
0,16
|
0,07
|
0,00
|
|
|
0,2
|
4,02
|
3,79
|
3,17
|
2,79
|
2,36
|
1,98
|
1,53
|
1,27
|
0,81
|
0,46
|
0,31
|
0,15
|
0,05
|
0,00
|
|
|
0,1
|
3,64
|
3,42
|
2,88
|
2,55
|
2,16
|
1,81
|
1,40
|
1,16
|
0,74
|
0,42
|
0,29
|
0,14
|
0,03
|
0,00
|
|
|
0,0
|
3,34
|
3,13
|
2,60
|
2,35
|
1,98
|
1,65
|
1,29
|
1,06
|
0,68
|
0,38
|
0,27
|
0,12
|
0,01
|
0,00
|
|
|
0,1
|
0,0
|
3,19
|
2,96
|
2,45
|
2,18
|
1,85
|
1,56
|
1,22
|
0,99
|
0,64
|
0,36
|
0,26
|
0,12
|
0,01
|
0,00
|
|
0,2
|
3,02
|
2,79
|
2,29
|
2,03
|
1,72
|
1,45
|
1,13
|
0,94
|
0,60
|
0,33
|
0,25
|
0,11
|
0,00
|
0,00
|
|
|
0,3
|
2,85
|
2,56
|
2,08
|
1,96
|
1,57
|
1,34
|
1,06
|
0,86
|
0,56
|
0,31
|
0,24
|
0,11
|
0,00
|
0,00
|
|
|
0,4
|
2,63
|
2,33
|
1,97
|
1,68
|
1,42
|
1,22
|
0,97
|
0,79
|
0,50
|
0,29
|
0,22
|
0,10
|
0,00
|
0,00
|
|
|
0,5
|
2,40
|
2,09
|
1,70
|
1,53
|
1,26
|
1,10
|
0,89
|
0,72
|
0,46
|
0,27
|
0,20
|
0,09
|
0,00
|
0,00
|
|
|
0,6
|
2,12
|
1,85
|
1,52
|
1,33
|
1,09
|
0,96
|
0,79
|
0,64
|
0,40
|
0,25
|
0,18
|
0,09
|
0,00
|
0,00
|
|
|
0,7
|
1,84
|
1,58
|
1,31
|
1,15
|
0,92
|
0,83
|
0,68
|
0,55
|
0,35
|
0,22
|
0,16
|
0,08
|
0,00
|
0,00
|
|
|
0,8
|
1,55
|
1,36
|
1,09
|
0,98
|
0,74
|
0,67
|
0,57
|
0,45
|
0,29
|
0,18
|
0,12
|
0,06
|
0,00
|
0,00
|
|
|
0,9
|
1,09
|
0,97
|
0,78
|
0,70
|
0,54
|
0,48
|
0,39
|
0,31
|
0,20
|
0,12
|
0,08
|
0,03
|
0,00
|
0,00
|
|
Таблица А.16
автокорреляции
r
(1), предназначенные для пересчета
критических значений статистики Стьюдента
|
r
(1)
|
0,00
|
0,01
|
0,02
|
0,03
|
0,04
|
0,05
|
0,06
|
0,07
|
0,08
|
0,09
|
|
0,0
|
1,00
|
1,00
|
1,01
|
1,02
|
1,02
|
1,03
|
1,04
|
1,05
|
1,06
|
1,07
|
|
0,1
|
1,07
|
1,08
|
1,09
|
1,10
|
1,11
|
1,12
|
1,13
|
1,14
|
1,16
|
1,17
|
|
0,2
|
1,18
|
1,19
|
1,20
|
1,22
|
1,23
|
1,24
|
1,26
|
1,27
|
1,29
|
1,31
|
|
0,3
|
1,33
|
1,34
|
1,35
|
1,37
|
1,39
|
1,41
|
1,42
|
1,44
|
1,46
|
1,49
|
|
0,4
|
1,51
|
1,52
|
1,54
|
1,56
|
1,59
|
1,67
|
1,63
|
1,65
|
1,68
|
1,70
|
|
0,5
|
1,72
|
1,75
|
1,78
|
1,81
|
1,84
|
1,88
|
1,92
|
1,95
|
1,99
|
2,03
|
|
0,6
|
2,06
|
2,07
|
2,13
|
2,17
|
2,21
|
2,24
|
2,28
|
2,32
|
2,36
|
2,40
|
Таблица Б.1
Ординаты кривых трехпараметрического гамма-распределения
Крицкого-Менкеля
|
P
, %
|
|
|||
|
0,1
|
0,2
|
0,3
|
0,4
|
|

|
||||
|
0,001
|
1,38
|
1,71
|
1,90
|
1,76
|
|
0,01
|
1,35
|
1,64
|
1,82
|
1,73
|
|
0,03
|
1,32
|
1,60
|
1,78
|
1,72
|
|
0,05
|
1,31
|
1,58
|
1,76
|
1,71
|
|
0,1
|
1,29
|
1,55
|
1,73
|
1,70
|
|
0,3
|
1,26
|
1,50
|
1,67
|
1,67
|
|
0,5
|
1,25
|
1,47
|
1,64
|
1,66
|
|
1
|
1,22
|
1,43
|
1,59
|
1,64
|
|
3
|
1,18
|
1,36
|
1,51
|
1,59
|
|
5
|
1,16
|
1,32
|
1,46
|
1,56
|
|
10
|
1,13
|
1,25
|
1,37
|
1,49
|
|
20
|
1,08
|
1,17
|
1,26
|
1,39
|
|
25
|
1,07
|
1,14
|
1,22
|
1,33
|
|
30
|
1,05
|
1,11
|
1,18
|
1,28
|
|
40
|
1,03
|
1,06
|
1,10
|
1,17
|
|
50
|
1,00
|
1,01
|
1,02
|
1,05
|
|
60
|
0,976
|
0,956
|
0,941
|
0,924
|
|
70
|
0,949
|
0,899
|
0,850
|
0,782
|
|
75
|
0,933
|
0,868
|
0,798
|
0,703
|
|
80
|
0,916
|
0,832
|
0,740
|
0,617
|
|
90
|
0,871
|
0,736
|
0,587
|
0,412
|
|
95
|
0,833
|
0,657
|
0,466
|
0,275
|
|
97
|
0,808
|
0,606
|
0,394
|
0,204
|
|
99
|
0,760
|
0,510
|
0,274
|
0,108
|
|
99,5
|
0,734
|
0,459
|
0,218
|
0,072
|
|
99,7
|
0,715
|
0,425
|
0,184
|
0,053
|
|
99,9
|
0,679
|
0,359
|
0,128
|
0,028
|
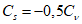
|
||||
|
0,001
|
1,39
|
1,76
|
2,02
|
2,11
|
|
0,01
|
1,36
|
1,68
|
1,93
|
2,03
|
|
0,03
|
1,33
|
1,63
|
1,87
|
1,98
|
|
0,05
|
1,32
|
1,61
|
1,84
|
1,98
|
|
0,1
|
1,30
|
1,58
|
1,80
|
1,96
|
|
0,3
|
1,27
|
1,52
|
1,73
|
1,86
|
|
0,5
|
1,25
|
1,49
|
1,69
|
1,83
|
|
1
|
1,23
|
1,45
|
1,64
|
1,77
|
|
3
|
1,19
|
1,37
|
1,53
|
1,67
|
|
5
|
1,16
|
1,32
|
1,47
|
1,61
|
|
10
|
1,13
|
1,25
|
1,38
|
1,51
|
|
20
|
1,08
|
1,17
|
1,26
|
1,37
|
|
25
|
1,07
|
1,14
|
1,21
|
1,31
|
|
30
|
1,05
|
1,11
|
1,17
|
1,25
|
|
40
|
1,03
|
1,06
|
1,09
|
1,14
|
|
50
|
1,00
|
1,00
|
1,01
|
1,03
|
|
60
|
0,975
|
0,952
|
0,932
|
0,910
|
|
70
|
0,948
|
0,897
|
0,844
|
0,780
|
|
75
|
0,933
|
0,866
|
0,795
|
0,708
|
|
80
|
0,916
|
0,831
|
0,740
|
0,629
|
|
90
|
0,871
|
0,739
|
0,597
|
0,435
|
|
95
|
0,834
|
0,663
|
0,484
|
0,301
|
|
97
|
0,810
|
0,615
|
0,415
|
0,230
|
|
99
|
0,764
|
0,525
|
0,299
|
0,128
|
|
99,5
|
0,739
|
0,476
|
0,243
|
0,089
|
|
99,7
|
0,721
|
0,444
|
0,208
|
0,068
|
|
99,9
|
0,686
|
0,381
|
0,150
|
0,038
|
|
P
, %
|
|
||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
|
C
s
= 0
|
|||||
|
0,001
|
1,41
|
1,81
|
2,15
|
2,38
|
2,42
|
|
0,01
|
1,37
|
1,72
|
2,03
|
2,25
|
2,33
|
|
0,03
|
1,34
|
1,67
|
1,96
|
2,18
|
2,27
|
|
0,05
|
1,33
|
1,64
|
1,93
|
2,15
|
2,24
|
|
0,1
|
1,31
|
1,60
|
1,88
|
2,09
|
2,20
|
|
0,3
|
1,27
|
1,54
|
1,79
|
2,00
|
2,12
|
|
0,5
|
1,26
|
1,51
|
1,74
|
1,95
|
2,08
|
|
1
|
1,23
|
1,46
|
1,68
|
1,87
|
2,01
|
|
3
|
1,19
|
1,37
|
1,56
|
1,73
|
1,88
|
|
5
|
1,16
|
1,33
|
1,49
|
1,65
|
1,80
|
|
10
|
1,13
|
1,26
|
1,39
|
1,52
|
1,66
|
|
20
|
1,08
|
1,17
|
1,26
|
1,36
|
1,47
|
|
25
|
1,07
|
1,14
|
1,21
|
1,29
|
1,39
|
|
30
|
1,05
|
1,11
|
1,16
|
1,23
|
1,31
|
|
40
|
1,03
|
1,05
|
1,08
|
1,12
|
1,16
|
|
50
|
1,00
|
1,00
|
1,00
|
1,01
|
1,01
|
|
60
|
0,975
|
0,949
|
0,923
|
0,895
|
0,855
|
|
70
|
0,947
|
0,894
|
0,838
|
0,775
|
0,690
|
|
75
|
0,932
|
0,864
|
0,792
|
0,709
|
0,603
|
|
80
|
0,916
|
0,830
|
0,740
|
0,637
|
0,511
|
|
90
|
0,872
|
0,742
|
0,606
|
0,459
|
0,305
|
|
95
|
0,835
|
0,670
|
0,501
|
0,331
|
0,182
|
|
97
|
0,812
|
0,624
|
0,436
|
0,261
|
0,125
|
|
99
|
0,768
|
0,540
|
0,326
|
0,156
|
0,055
|
|
99,5
|
0,743
|
0,494
|
0,271
|
0,112
|
0,033
|
|
99,7
|
0,726
|
0,464
|
0,237
|
0,088
|
0,023
|
|
99,9
|
0,693
|
0,405
|
0,178
|
0,053
|
0,010
|
|
P
, %
|
|
||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
|

|
|||||||
|
0,001
|
1,42
|
1,87
|
2,29
|
2,66
|
2,94
|
3,08
|
3,00
|
|
0,01
|
1,38
|
1,76
|
2,13
|
2,47
|
2,74
|
2,91
|
2,89
|
|
0,03
|
1,35
|
1,71
|
2,05
|
2,37
|
2,64
|
2,81
|
2,83
|
|
0,05
|
1,34
|
1,68
|
2,01
|
2,32
|
2,58
|
2,76
|
2,79
|
|
0,1
|
1,31
|
1,63
|
1,95
|
2,25
|
2,50
|
2,69
|
2,74
|
|
0,3
|
1,28
|
1,56
|
1,85
|
2,12
|
2,36
|
2,55
|
2,64
|
|
0,5
|
1,26
|
1,53
|
1,79
|
2,05
|
2,28
|
2,48
|
2,59
|
|
1
|
1,24
|
1,48
|
1,72
|
1,95
|
2,17
|
2,37
|
2,50
|
|
3
|
1,19
|
1,38
|
1,58
|
1,78
|
1,97
|
2,16
|
2,33
|
|
5
|
1,17
|
1,33
|
1,51
|
1,68
|
1,86
|
2,03
|
2,22
|
|
10
|
1,13
|
1,26
|
1,39
|
1,53
|
1,67
|
1,83
|
2,01
|
|
20
|
1,08
|
1,17
|
1,25
|
1,35
|
1,44
|
1,56
|
1,70
|
|
25
|
1,07
|
1,13
|
1,20
|
1,27
|
1,35
|
1,45
|
1,56
|
|
30
|
1,05
|
1,10
|
1,16
|
1,21
|
1,27
|
1,34
|
1,42
|
|
40
|
1,02
|
1,05
|
1,07
|
1,10
|
1,12
|
1,15
|
1,16
|
|
50
|
0,999
|
0,997
|
0,993
|
0,988
|
0,98
|
0,962
|
0,920
|
|
60
|
0,974
|
0,946
|
0,915
|
0,881
|
0,839
|
0,780
|
0,690
|
|
70
|
0,947
|
0,882
|
0,834
|
0,769
|
0,693
|
0,596
|
0,476
|
|
75
|
0,932
|
0,862
|
0,789
|
0,709
|
0,615
|
0,503
|
0,376
|
|
80
|
0,915
|
0,829
|
0,740
|
0,643
|
0,533
|
0,409
|
0,282
|
|
90
|
0,872
|
0,744
|
0,615
|
0,480
|
0,343
|
0,215
|
0,115
|
|
95
|
0,837
|
0,676
|
0,517
|
0,362
|
0,221
|
0,113
|
0,047
|
|
97
|
0,814
|
0,633
|
0,458
|
0,295
|
0,16
|
0,07
|
0,024
|
|
99
|
0,772
|
0,554
|
0,354
|
0,189
|
0,08
|
0,025
|
0,006
|
|
99,5
|
0,748
|
0,511
|
0,302
|
0,144
|
0,051
|
0,013
|
0,002
|
|
99,7
|
0,732
|
0,482
|
0,269
|
0,117
|
0,037
|
0,008
|
0,001
|
|
P
, %
|
|
||||||||||
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
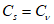
|
|||||||||||
|
0,001
|
1
|
1,46
|
1,94
|
2,46
|
2,97
|
3,47
|
3,94
|
4,36
|
4,73
|
5,06
|
5,35
|
|
0,01
|
1
|
1,38
|
1,81
|
2,26
|
2,70
|
3,15
|
3,57
|
3,95
|
4,31
|
4,64
|
4,92
|
|
0,03
|
1
|
1,35
|
1,74
|
2,15
|
2,56
|
2,97
|
3,37
|
3,74
|
4,09
|
4,41
|
4,69
|
|
0,05
|
1
|
1,34
|
1,71
|
2,10
|
2,49
|
2,89
|
3,27
|
3,64
|
3,98
|
4,29
|
4,58
|
|
0,1
|
1
|
1,32
|
1,67
|
2,03
|
2,40
|
2,77
|
3,13
|
3,48
|
3,82
|
4,13
|
4,42
|
|
0,3
|
1
|
1,28
|
1,59
|
1,91
|
2,23
|
2,56
|
2,89
|
3,21
|
3,53
|
3,84
|
4,14
|
|
0,5
|
1
|
1,27
|
1,55
|
1,84
|
2,15
|
2,46
|
2,77
|
3,08
|
3,38
|
3,69
|
3,99
|
|
1
|
1
|
1,24
|
1,49
|
1,76
|
2,03
|
2,30
|
2,59
|
2,88
|
3,16
|
3,46
|
3,75
|
|
3
|
1
|
1,19
|
1,39
|
1,60
|
1,82
|
2,04
|
2,27
|
2,50
|
2,75
|
3,01
|
3,29
|
|
5
|
1
|
1,17
|
1,34
|
1,52
|
1,70
|
1,90
|
2,10
|
2,30
|
2,53
|
2,76
|
3,02
|
|
10
|
1
|
1,13
|
1,26
|
1,40
|
1,54
|
1,68
|
1,83
|
1,99
|
2,16
|
2,35
|
2,55
|
|
20
|
1
|
1,08
|
1,17
|
1,25
|
1,34
|
1,42
|
1,51
|
1,60
|
1,70
|
1,80
|
1,90
|
|
25
|
1
|
1,07
|
1,13
|
1,20
|
1,26
|
1,33
|
1,39
|
1,46
|
1,52
|
1,59
|
1,64
|
|
30
|
1
|
1,05
|
1,10
|
1,15
|
1,20
|
1,24
|
1,29
|
1,33
|
1,37
|
1,39
|
1,40
|
|
40
|
1
|
1,02
|
1,04
|
1,06
|
1,08
|
1,09
|
1,10
|
1,10
|
1,08
|
1,05
|
0,995
|
|
50
|
1
|
0,998
|
0,993
|
0,985
|
0,972
|
0,954
|
0,928
|
0,891
|
0,836
|
0,76
|
0,665
|
|
60
|
1
|
0,973
|
0,943
|
0,909
|
0,870
|
0,824
|
0,768
|
0,698
|
0,613
|
0,512
|
0,406
|
|
70
|
1
|
0,946
|
0,890
|
0,830
|
0,764
|
0,692
|
0,609
|
0,515
|
0,413
|
0,309
|
0,215
|
|
75
|
1
|
0,932
|
0,861
|
0,787
|
0,708
|
0,622
|
0,528
|
0,426
|
0,321
|
0,224
|
0,144
|
|
80
|
1
|
0,915
|
0,829
|
0,740
|
0,648
|
0,549
|
0,445
|
0,338
|
0,237
|
0,151
|
0,088
|
|
90
|
1
|
0,873
|
0,748
|
0,623
|
0,500
|
0,378
|
0,264
|
0,165
|
0,092
|
0,045
|
0,019
|
|
95
|
1
|
0,838
|
0,683
|
0,533
|
0,392
|
0,263
|
0,157
|
0,081
|
0,036
|
0,013
|
0,004
|
|
97
|
1
|
0,816
|
0,642
|
0,478
|
0,329
|
0,202
|
0,107
|
0,048
|
0,018
|
0,005
|
0,001
|
|
99
|
1
|
0,775
|
0,568
|
0,383
|
0,229
|
0,115
|
0,047
|
0,015
|
0,004
|
0,001
|
0,1
|
|
99,5
|
1
|
0,752
|
0,528
|
0,335
|
0,182
|
0,081
|
0,028
|
0,008
|
0,002
|
0,2
|
0,3
|
|
99,7
|
1
|
0,737
|
0,502
|
0,303
|
0,154
|
0,062
|
0,019
|
0,004
|
0,001
|
0,9
|
0,1
|
|
99,9
|
1
|
0,707
|
0,451
|
0,247
|
0,108
|
0,036
|
0,008
|
0,001
|
2·10
-3
|
0,1
|
0,2
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|
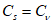
|
||||||||||
|
0,001
|
5,58
|
5,76
|
5,90
|
6,02
|
6,12
|
6,2
|
6,26
|
6,32
|
6,36
|
6,40
|
|
0,01
|
5,16
|
5,34
|
5,46
|
5,58
|
5,68
|
5,76
|
5,82
|
5,88
|
5,92
|
5,96
|
|
0,03
|
4,94
|
5,16
|
5,29
|
5,42
|
5,51
|
5,58
|
5,65
|
5,70
|
5,74
|
5,78
|
|
0,05
|
4,83
|
5,06
|
5,20
|
5,32
|
5,42
|
5,49
|
5,56
|
5,62
|
5,67
|
5,72
|
|
0,1
|
4,69
|
4,92
|
5,06
|
5,18
|
5,29
|
5,37
|
5,44
|
5,49
|
5,54
|
5,58
|
|
0,3
|
4,44
|
4,74
|
4,92
|
5,06
|
5,16
|
5,24
|
5,31
|
5,36
|
5,42
|
5,46
|
|
0,5
|
4,29
|
4,58
|
4,75
|
4,91
|
5,02
|
5,11
|
5,18
|
5,24
|
5,28
|
5,32
|
|
1
|
4,06
|
4,36
|
4,55
|
4,72
|
4,84
|
4,94
|
5,00
|
5,07
|
5,12
|
5,16
|
|
3
|
3,59
|
3,92
|
4,14
|
4,33
|
4,46
|
4,58
|
4,68
|
4,76
|
4,84
|
4,92
|
|
5
|
3,31
|
3,63
|
3,84
|
4,02
|
4,16
|
4,28
|
4,40
|
4,50
|
4,60
|
4,69
|
|
10
|
2,78
|
3,03
|
3,26
|
3,46
|
3,64
|
2,56
|
3,94
|
4,05
|
4,15
|
4,25
|
|
20
|
2,00
|
2,10
|
2,20
|
2,32
|
2,44
|
1,66
|
2,67
|
2,80
|
2,92
|
3,03
|
|
25
|
1,68
|
1,69
|
1,70
|
1,70
|
1,68
|
0,96
|
1,61
|
1,56
|
1,51
|
1,46
|
|
30
|
1,39
|
1,34
|
1,26
|
1,17
|
1,07
|
0,38
|
0,84
|
0,72
|
0,60
|
0,45
|
|
40
|
0,916
|
0,808
|
0,72
|
0,60
|
0,50
|
0,15
|
0,28
|
0,20
|
0,11
|
0,04
|
|
50
|
0,559
|
0,446
|
0,34
|
0,26
|
0,20
|
0,075
|
0,105
|
0,07
|
0,04
|
0,01
|
|
60
|
0,306
|
0,216
|
0,19
|
0,13
|
0,10
|
0,025
|
0,055
|
0,035
|
0,015
|
0
|
|
70
|
0,141
|
0,085
|
0,06
|
0,045
|
0,035
|
0,005
|
0,015
|
0,01
|
0
|
0
|
|
75
|
0,086
|
0,046
|
0,025
|
0,02
|
0,01
|
0
|
0
|
0
|
0
|
0
|
|
80
|
0,047
|
0,023
|
0,015
|
0,005
|
0
|
0
|
0
|
0
|
0
|
0
|
|
90
|
0,007
|
0,002
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
95
|
0,001
|
3·10
-4
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
97
|
0,0003
|
6·10
-5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
99
|
2·10
-5
|
5·10
-6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
99,5
|
5·10
-6
|
6·10
-7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
99,7
|
2·10
-6
|
2·10
-7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
99,9
|
1·10
-7
|
7·10
-9
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
P
, %
|
|
||||||||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
|

|
|||||||||||||||
|
0,01
|
1,47
|
2,01
|
2,63
|
3,3
|
4,03
|
4,81
|
5,64
|
6,5
|
7,41
|
8,39
|
9,41
|
10,4
|
11,5
|
12,7
|
13,9
|
|
0,01
|
1,4
|
1,86
|
2,38
|
2,94
|
3,55
|
4,19
|
4,88
|
5,61
|
6,38
|
7,19
|
8,03
|
8,92
|
9,83
|
10,8
|
11,8
|
|
0,03
|
1,37
|
1,79
|
2,26
|
2,76
|
3,3
|
3,88
|
4,5
|
5,14
|
5,82
|
6,56
|
7,33
|
8,13
|
8,96
|
9,8
|
10,7
|
|
0,05
|
1,32
|
1,75
|
2,2
|
2,68
|
3,18
|
3,73
|
4,31
|
4,93
|
5,58
|
6,26
|
6,95
|
7,67
|
8,43
|
9,22
|
10,1
|
|
0,1
|
1,33
|
1,70
|
2,11
|
2,54
|
3,02
|
3,52
|
4,06
|
4,62
|
5,22
|
5,84
|
6,50
|
7,18
|
7,88
|
8,61
|
9,38
|
|
0,3
|
1,29
|
1,61
|
1,97
|
2,34
|
2,74
|
3,17
|
3,62
|
4,1
|
4,61
|
5,14
|
5,72
|
6,32
|
6,95
|
7,60
|
8,25
|
|
0,5
|
1,27
|
1,57
|
1,90
|
2,24
|
2,61
|
3,0
|
3,41
|
3,85
|
4,31
|
4,80
|
5,32
|
5,87
|
6,44
|
7,04
|
7,66
|
|
1
|
1,24
|
1,51
|
1,79
|
2,09
|
2,42
|
2,76
|
3,11
|
3,49
|
3,89
|
4,30
|
4,74
|
5,21
|
5,70
|
6,24
|
6,78
|
|
3
|
1,19
|
1,40
|
1,62
|
1,85
|
2,09
|
2,34
|
2,6
|
2,88
|
3,16
|
3,46
|
3,78
|
4,12
|
4,48
|
4,86
|
5,27
|
|
5
|
1,17
|
1,35
|
1,53
|
1,72
|
1,92
|
2,13
|
2,34
|
2,57
|
2,80
|
3,03
|
3,28
|
3,55
|
3,83
|
4,12
|
4,44
|
|
10
|
1,13
|
1,26
|
1,40
|
1,54
|
1,68
|
1,82
|
1,97
|
2,11
|
2,26
|
2,41
|
2,56
|
2,71
|
2,86
|
3,00
|
3,13
|
|
20
|
1,08
|
1,16
|
1,25
|
1,32
|
1,4
|
1,47
|
1,54
|
1,61
|
1,67
|
1,72
|
1,76
|
1,80
|
1,82
|
1,83
|
1,83
|
|
25
|
1,07
|
1,13
|
1,19
|
1,25
|
1,3
|
1,35
|
1,39
|
1,43
|
1,46
|
1,48
|
1,49
|
1,49
|
1,48
|
1,46
|
1,43
|
|
30
|
1,05
|
1,10
|
1,14
|
1,18
|
1,21
|
1,24
|
1,27
|
1,28
|
1,28
|
1,28
|
1,26
|
1,24
|
1,20
|
1,16
|
1,10
|
|
40
|
1,02
|
1,04
|
1,06
|
1,06
|
1,06
|
1,06
|
1,05
|
1,03
|
0,994
|
0,952
|
0,901
|
0,84
|
0,766
|
0,692
|
0,622
|
|
50
|
0,998
|
0,990
|
0,977
|
0,958
|
0,934
|
0,902
|
0,862
|
0,814
|
0,756
|
0,690
|
0,618
|
0,541
|
0,463
|
0,388
|
0,320
|
|
60
|
0,972
|
0,940
|
0,903
|
0,860
|
0,812
|
0,757
|
0,695
|
0,627
|
0,553
|
0,475
|
0,398
|
0,324
|
0,253
|
0,193
|
0,142
|
|
70
|
0,946
|
0,888
|
0,826
|
0,760
|
0,690
|
0,616
|
0,538
|
0,457
|
0,376
|
0,298
|
0,228
|
0,168
|
0,118
|
0,079
|
0,051
|
|
75
|
0,931
|
0,860
|
0,785
|
0,708
|
0,630
|
0,545
|
0,460
|
0,377
|
0,297
|
0,223
|
0,161
|
0,111
|
0,072
|
0,045
|
0,027
|
|
80
|
0,915
|
0,829
|
0,741
|
0,652
|
0,562
|
0,472
|
0,384
|
0,299
|
0,223
|
0,156
|
0,150
|
0,067
|
0,039
|
0,220
|
0,012
|
|
90
|
0,874
|
0,751
|
0,632
|
0,518
|
0,409
|
0,310
|
0,222
|
0,148
|
0,092
|
0,053
|
0,028
|
0,014
|
0,006
|
0,003
|
0,001
|
|
95
|
0,840
|
0,689
|
0,548
|
0,419
|
0,305
|
0,207
|
0,130
|
0,074
|
0,038
|
0,018
|
0,008
|
0,003
|
0,001
|
0,3·10
-4
|
0,2·10
-3
|
|
97
|
0,819
|
0,651
|
0,498
|
0,363
|
0,247
|
0,155
|
0,088
|
0,045
|
0,020
|
0,008
|
0,003
|
0,001
|
0,3·10
-3
|
0,8·10
-3
|
0,3·10
-4
|
|
99
|
0,780
|
0,581
|
0,410
|
0,268
|
0,160
|
0,084
|
0,038
|
0,015
|
0,005
|
0,001
|
0,4·10
-3
|
0,1·10
-3
|
0,4·10
-4
|
0,8·10
-5
|
0,2·10
-5
|
|
99,5
|
0,758
|
0,545
|
0,366
|
0,223
|
0,122
|
0,057
|
0,023
|
0,008
|
0,002
|
0,5·10
-3
|
0,1·10
-3
|
0,1·10
-4
|
0,9·10
-5
|
0,6·10
-6
|
0,2·10
-6
|
|
99,7
|
0,744
|
0,520
|
0,337
|
0,205
|
0,108
|
0,043
|
0,016
|
0,005
|
0,001
|
0,2·10
-3
|
0,5·10
-4
|
0,4·10
-4
|
0,1·10
-5
|
0,4·10
-6
|
0,8·10
-7
|
|
99,9
|
0,714
|
0,474
|
0,284
|
0,152
|
0,066
|
0,024
|
0,007
|
0,001
|
0,3·10
-3
|
0,4·10
-4
|
0,6·10
-5
|
0,1·10
-5
|
0,2·10
-6
|
0,3·10
-7
|
0,2·10
-8
|
|
P
, %
|
|
||||||||||
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
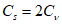
|
|||||||||||
|
0,001
|
1
|
1,49
|
2,09
|
2,82
|
3,68
|
4,67
|
5,78
|
7,03
|
8,4
|
9,89
|
11,5
|
|
0,01
|
1
|
1,42
|
1,92
|
2,52
|
3,20
|
3,98
|
4,85
|
5,81
|
6,85
|
7,98
|
9,21
|
|
0,03
|
1
|
1,38
|
1,83
|
2,36
|
2,96
|
3,64
|
4,39
|
5,22
|
6,11
|
7,08
|
8,11
|
|
0,05
|
1
|
1,36
|
1,79
|
2,29
|
2,85
|
3,48
|
4,18
|
4,95
|
5,77
|
6,66
|
7,60
|
|
0,1
|
1
|
1,34
|
1,73
|
2,19
|
2,70
|
3,27
|
3,87
|
4,56
|
5,30
|
6,08
|
6,91
|
|
0,3
|
1
|
1,30
|
1,64
|
2,02
|
2,45
|
2,91
|
3,42
|
3,96
|
4,55
|
5,16
|
5,81
|
|
0,5
|
1
|
1,28
|
1,59
|
1,94
|
2,32
|
2,74
|
3,20
|
3,68
|
4,19
|
4,74
|
5,30
|
|
1
|
1
|
1,25
|
1,52
|
1,82
|
2,16
|
2,51
|
2,89
|
3,29
|
3,71
|
4,15
|
4,60
|
|
3
|
1
|
1,20
|
1,41
|
1,64
|
1,87
|
2,13
|
2,39
|
2,66
|
2,94
|
3,21
|
3,51
|
|
5
|
1
|
1,17
|
1,35
|
1,54
|
1,74
|
1,94
|
2,15
|
2,36
|
2,57
|
2,78
|
3,00
|
|
10
|
1
|
1,13
|
1,26
|
1,40
|
1,54
|
1,67
|
1,80
|
1,94
|
2,06
|
2,19
|
2,30
|
|
20
|
1
|
1,08
|
1,16
|
1,24
|
1,31
|
1,38
|
1,44
|
1,5
|
1,54
|
1,58
|
1,61
|
|
25
|
1
|
1,06
|
1,13
|
1,18
|
1,23
|
1,28
|
1,31
|
1,34
|
1,37
|
1,38
|
1,39
|
|
30
|
1
|
1,05
|
1,09
|
1,13
|
1,16
|
1,19
|
1,21
|
1,22
|
1,22
|
1,22
|
1,20
|
|
40
|
1
|
1,02
|
1,04
|
1,05
|
1,05
|
1,04
|
1,03
|
1,01
|
0,984
|
0,955
|
0,916
|
|
50
|
1
|
0,997
|
0,986
|
0,970
|
0,948
|
0,918
|
0,886
|
0,846
|
0,800
|
0,748
|
0,693
|
|
60
|
1
|
0,972
|
0,938
|
0,898
|
0,852
|
0,803
|
0,748
|
0,692
|
0,632
|
0,568
|
0,511
|
|
70
|
1
|
0,945
|
0,886
|
0,823
|
0,760
|
0,691
|
0,622
|
0,552
|
0,488
|
0,424
|
0,357
|
|
75
|
1
|
0,931
|
0,858
|
0,784
|
0,708
|
0,634
|
0,556
|
0,489
|
0,416
|
0,352
|
0,288
|
|
80
|
1
|
0,915
|
0,830
|
0,745
|
0,656
|
0,574
|
0,496
|
0,419
|
0,352
|
0,280
|
0,223
|
|
90
|
1
|
0,873
|
0,754
|
0,640
|
0,532
|
0,436
|
0,352
|
0,272
|
0,208
|
0,154
|
0,150
|
|
95
|
1
|
0,842
|
0,696
|
0,565
|
0,448
|
0,342
|
0,256
|
0,181
|
0,120
|
0,082
|
0,051
|
|
97
|
1
|
0,821
|
0,660
|
0,517
|
0,392
|
0,288
|
0,202
|
0,139
|
0,088
|
0,046
|
0,030
|
|
99
|
1
|
0,782
|
0,594
|
0,436
|
0,304
|
0,206
|
0,130
|
0,076
|
0,04
|
0,019
|
0,010
|
|
99,5
|
1
|
0,761
|
0,560
|
0,394
|
0,269
|
0,166
|
0,099
|
0,054
|
0,027
|
0,012
|
0,005
|
|
99,7
|
1
|
0,748
|
0,537
|
0,374
|
0,240
|
0,144
|
0,082
|
0,042
|
0,019
|
0,008
|
0,003
|
|
99,9
|
1
|
0,719
|
0,492
|
0,319
|
0,192
|
0,107
|
0,052
|
0,027
|
0,008
|
0,004
|
0,001
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|
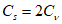
|
||||||||||
|
0,001
|
13,2
|
15,1
|
17,2
|
19,3
|
21,6
|
23,9
|
26,2
|
28,6
|
31,3
|
34,4
|
|
0,01
|
10,5
|
11,8
|
13,2
|
14,7
|
16,4
|
18,2
|
20,2
|
22,2
|
24,4
|
26,6
|
|
0,03
|
9,20
|
10,3
|
11,6
|
12,9
|
14,3
|
15,6
|
17,0
|
18,5
|
20,0
|
21,4
|
|
0,05
|
8,61
|
9,65
|
10,8
|
11,9
|
13,1
|
14,2
|
15,5
|
16,7
|
18
|
19,4
|
|
0,1
|
7,75
|
8,65
|
9,60
|
10,6
|
11,6
|
12,5
|
13,5
|
14,6
|
15,8
|
17,0
|
|
0,3
|
6,47
|
7,10
|
7,98
|
8,70
|
9,50
|
10,5
|
11,0
|
11,9
|
12,7
|
13,6
|
|
0,5
|
5,90
|
6,50
|
7,13
|
7,80
|
8,42
|
9,00
|
9,50
|
10,1
|
10,8
|
11,4
|
|
1
|
5,05
|
5,53
|
6,02
|
6,55
|
7,08
|
7,50
|
8,00
|
8,60
|
9,20
|
9,80
|
|
3
|
3,80
|
4,12
|
4,42
|
4,71
|
4,98
|
5,20
|
5,50
|
5,80
|
6,20
|
6,50
|
|
5
|
3,22
|
3,40
|
3,60
|
3,80
|
3,96
|
4,00
|
4,30
|
4,50
|
4,70
|
5,00
|
|
10
|
2,40
|
2,50
|
2,57
|
2,64
|
2,70
|
2,70
|
2,60
|
2,60
|
2,60
|
2,6
|
|
20
|
1,62
|
1,63
|
1,62
|
1,61
|
1,59
|
1,60
|
1,60
|
1,56
|
1,50
|
2,5
|
|
25
|
1,39
|
1,35
|
1,33
|
1,31
|
1,28
|
1,26
|
1,24
|
1,22
|
1,20
|
1,18
|
|
30
|
1,18
|
1,14
|
1,11
|
1,08
|
1,04
|
1,02
|
0,98
|
0,95
|
0,92
|
0,89
|
|
40
|
0,87
|
0,83
|
0,77
|
0,725
|
0,67
|
0,625
|
0,58
|
0,53
|
0,48
|
0,44
|
|
50
|
0,64
|
0,58
|
0,52
|
0,46
|
0,405
|
0,355
|
0,310
|
0,265
|
0,230
|
0,200
|
|
60
|
0,450
|
0,390
|
0,334
|
0,283
|
0,234
|
0,190
|
0,16
|
0,130
|
0,105
|
0,085
|
|
70
|
0,300
|
0,250
|
0,203
|
0,155
|
0,120
|
0,090
|
0,070
|
0,060
|
0,050
|
0,045
|
|
75
|
0,241
|
0,193
|
0,146
|
0,106
|
0,077
|
0,060
|
0,050
|
0,040
|
0,030
|
0,025
|
|
80
|
0,175
|
0,130
|
0,094
|
0,065
|
0,046
|
0,035
|
0,027
|
0,020
|
0,015
|
0,01
|
|
90
|
0,074
|
0,049
|
0,030
|
0,016
|
0,009
|
0,005
|
0,004
|
0,003
|
0,002
|
0,001
|
|
95
|
0,030
|
0,016
|
0,009
|
0,004
|
0,002
|
0,001
|
0,0002
|
8·10
-5
|
5·10
-5
|
2·10
-5
|
|
97
|
0,016
|
0,008
|
0,004
|
0,002
|
0,001
|
2·10
-4
|
8·10
-5
|
5·10
-5
|
2-10
-5
|
5·10
-6
|
|
99
|
0,005
|
0,002
|
0,001
|
2·10
-4
|
8·10
-5
|
5·10
-5
|
2·10
-5
|
1·10
-5
|
5·10
-6
|
1·10
-6
|
|
99,5
|
0,002
|
0,001
|
2·10
-4
|
5·10
-5
|
2·10
-5
|
5·10
-6
|
1·10
-6
|
0
|
0
|
0
|
|
99,7
|
0,001
|
3·10
-4
|
8·10
-5
|
2·10
-5
|
1·10
-5
|
1·10
-6
|
0
|
0
|
0
|
0
|
|
99,9
|
2·10
-4
|
4·10
-5
|
1·10
-5
|
5·10
-6
|
1·10
-6
|
0
|
0
|
0
|
0
|
0
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
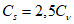
|
||||||||||
|
0,001
|
1,52
|
2,18
|
3,05
|
4,13
|
5,41
|
6,90
|
8,61
|
10,5
|
12,6
|
14,8
|
|
0,01
|
1,44
|
1,98
|
2,67
|
3,49
|
4,45
|
5,54
|
6,76
|
8,10
|
9,55
|
11,1
|
|
0,03
|
1,40
|
1,88
|
2,48
|
3,18
|
4,00
|
4,91
|
5,93
|
7,02
|
8,20
|
9,46
|
|
0,05
|
1,38
|
1,83
|
2,39
|
3,04
|
3,79
|
4,62
|
5,54
|
6,53
|
7,59
|
8,72
|
|
0,1
|
1,35
|
1,77
|
2,27
|
2,85
|
3,51
|
4,24
|
5,04
|
5,90
|
6,80
|
7,76
|
|
0,3
|
1,30
|
1,66
|
2,08
|
2,55
|
3,07
|
3,64
|
4,26
|
4,91
|
5,58
|
6,28
|
|
0,5
|
1,28
|
1,61
|
1,99
|
2,41
|
2,87
|
3,36
|
3,90
|
4,46
|
5,03
|
5,63
|
|
1
|
1,25
|
1,54
|
1,86
|
2,21
|
2,59
|
3,00
|
3,42
|
3,87
|
4,32
|
4,78
|
|
3
|
1,20
|
1,42
|
1,65
|
1,90
|
2,15
|
2,42
|
2,69
|
2,96
|
3,23
|
3,50
|
|
5
|
1,17
|
1,35
|
1,55
|
1,74
|
1,95
|
2,15
|
2,35
|
2,55
|
2,75
|
2,94
|
|
10
|
1,13
|
1,26
|
1,4
|
1,53
|
1,66
|
1,78
|
1,9
|
2,01
|
2,12
|
2,22
|
|
20
|
1,08
|
1,16
|
1,23
|
1,30
|
1,36
|
1,14
|
1,45
|
1,49
|
1,52
|
1,54
|
|
25
|
1,07
|
1,12
|
1,18
|
1,22
|
1,26
|
1,28
|
1,31
|
1,32
|
1,33
|
1,33
|
|
30
|
1,05
|
1,09
|
1,13
|
1,15
|
1,17
|
1,18
|
1,18
|
1,18
|
1,17
|
1,16
|
|
40
|
1,02
|
1,04
|
1,04
|
1,04
|
1,03
|
1,01
|
0,989
|
0,962
|
0,93
|
0,895
|
|
50
|
0,997
|
0,984
|
0,964
|
0,938
|
0,906
|
0,87
|
0,83
|
0,787
|
0,742
|
0,695
|
|
60
|
0,972
|
0,935
|
0,893
|
0,847
|
0,797
|
0,745
|
0,692
|
0,639
|
0,586
|
0,533
|
|
70
|
0,945
|
0,885
|
0,822
|
0,758
|
0,693
|
0,629
|
0,567
|
0,506
|
0,449
|
0,395
|
|
75
|
0,931
|
0,858
|
0,785
|
0,712
|
0,640
|
0,571
|
0,505
|
0,443
|
0,385
|
0,332
|
|
80
|
0,915
|
0,83
|
0,745
|
0,663
|
0,585
|
0,512
|
0,444
|
0,381
|
0,324
|
0,272
|
|
90
|
0,875
|
0,757
|
0,648
|
0,549
|
0,459
|
0,381
|
0,310
|
0,250
|
0,198
|
0,155
|
|
95
|
0,843
|
0,702
|
0,576
|
0,467
|
0,373
|
0,293
|
0,227
|
0,172
|
0,128
|
0,093
|
|
97
|
0,823
|
0,667
|
0,533
|
0,420
|
0,325
|
0,247
|
0,184
|
0,134
|
0,095
|
0,065
|
|
99
|
0,784
|
0,606
|
0,459
|
0,341
|
0,248
|
0,175
|
0,120
|
0,080
|
0,052
|
0,032
|
|
99,5
|
0,765
|
0,574
|
0,422
|
0,303
|
0,212
|
0,143
|
0,094
|
0,059
|
0,036
|
0,02
|
|
99,7
|
0,752
|
0,558
|
0,398
|
0,278
|
0,189
|
0,123
|
0,078
|
0,047
|
0,028
|
0,015
|
|
99,9
|
0,727
|
0,513
|
0,353
|
0,235
|
0,151
|
0,093
|
0,055
|
0,03
|
0,016
|
0,008
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|
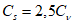
|
||||||||||
|
0,001
|
17,2
|
19,9
|
22,6
|
25,6
|
28,7
|
32,1
|
35,8
|
39,7
|
43,9
|
48,4
|
|
0,01
|
12,8
|
14,6
|
16,4
|
18,4
|
20,4
|
22,5
|
24,7
|
27,0
|
29,3
|
31,9
|
|
0,03
|
10,8
|
12,2
|
13,7
|
15,2
|
16,8
|
18,5
|
20,2
|
22,1
|
24,0
|
26,0
|
|
0,05
|
9,92
|
11,2
|
12,5
|
13,8
|
15,2
|
16,7
|
18,2
|
19,8
|
21,5
|
23,2
|
|
0,1
|
8,76
|
9,81
|
10,9
|
12,0
|
13,2
|
14,4
|
15,7
|
17,0
|
18,4
|
19,8
|
|
0,3
|
7,02
|
7,78
|
8,56
|
9,36
|
10,2
|
11,1
|
12,0
|
13,0
|
14,1
|
15,2
|
|
0,5
|
6,25
|
6,89
|
7,54
|
8,20
|
8,88
|
9,56
|
10,3
|
11,0
|
11,8
|
12,6
|
|
1
|
5,26
|
5,73
|
6,22
|
6,71
|
7,20
|
7,70
|
8,20
|
8,71
|
9,22
|
9,74
|
|
3
|
3,77
|
4,04
|
4,30
|
4,56
|
4,81
|
5,06
|
5,30
|
5,54
|
5,78
|
6,01
|
|
5
|
3,13
|
3,31
|
3,48
|
3,65
|
3,81
|
3,96
|
4,10
|
4,26
|
4,39
|
4,52
|
|
10
|
2,31
|
2,39
|
2,46
|
2,53
|
2,59
|
2,64
|
2,69
|
2,73
|
2,76
|
2,79
|
|
20
|
1,55
|
1,56
|
1,56
|
1,55
|
1,54
|
1,52
|
1,50
|
1,47
|
1,44
|
1,41
|
|
25
|
1,32
|
1,31
|
1,29
|
1,27
|
1,24
|
1,21
|
1,17
|
1,14
|
1,10
|
1,05
|
|
30
|
1,14
|
1,11
|
1,08
|
1,05
|
1,01
|
0,972
|
0,931
|
0,888
|
0,843
|
0,797
|
|
40
|
0,857
|
0,816
|
0,773
|
0,729
|
0,684
|
0,638
|
0,592
|
0,545
|
0,497
|
0,447
|
|
50
|
0,648
|
0,600
|
0,552
|
0,505
|
0,459
|
0,415
|
0,373
|
0,332
|
0,295
|
0,259
|
|
60
|
0,482
|
0,432
|
0,385
|
0,34
|
0,298
|
0,259
|
0,224
|
0,191
|
0,162
|
0,136
|
|
70
|
0,344
|
0,297
|
0,254
|
0,215
|
0,180
|
0,149
|
0,122
|
0,099
|
0,079
|
0,062
|
|
75
|
0,283
|
0,238
|
0,199
|
0,164
|
0,133
|
0,107
|
0,085
|
0,066
|
0,051
|
0,039
|
|
80
|
0,226
|
0,185
|
0,149
|
0,119
|
0,094
|
0,072
|
0,055
|
0,041
|
0,030
|
0,022
|
|
90
|
0,118
|
0,089
|
0,066
|
0,047
|
0,033
|
0,023
|
0,015
|
0,010
|
0,006
|
0,004
|
|
95
|
0,066
|
0,046
|
0,030
|
0,020
|
0,012
|
0,008
|
0,004
|
0,002
|
0,001
|
0,001
|
|
97
|
0,044
|
0,028
|
0,018
|
0,011
|
0,006
|
0,003
|
0,002
|
0,001
|
4·10
-4
|
2·10
-4
|
|
99
|
0,019
|
0,011
|
0,006
|
0,003
|
0,001
|
0,001
|
3·10
-4
|
1·10
-4
|
4·10
-5
|
2·10
-5
|
|
99,5
|
0,011
|
0,006
|
0,003
|
0,001
|
0,5·10
-3
|
0,2·10
-3
|
0,8·10
-4
|
0,3·10
-4
|
0,1·10
-4
|
0,3·10
-5
|
|
99,7
|
0,008
|
0,004
|
0,002
|
0,7·10
-3
|
0,3·10
-3
|
0,1·10
-3
|
0,4·10
-5
|
0,1·10
-4
|
0,3·10
-5
|
0,1·10
-5
|
|
P
, %
|
|
||||||||||
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
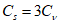
|
|||||||||||
|
0,001
|
1
|
1,54
|
2,29
|
3,32
|
4,63
|
6,24
|
8,14
|
10,3
|
12,7
|
15,4
|
18,2
|
|
0,01
|
1
|
1,46
|
2,05
|
2,83
|
3,80
|
4,94
|
6,26
|
7,70
|
9,30
|
11,0
|
12,8
|
|
0,03
|
1
|
1,41
|
1,93
|
2,59
|
3,42
|
4,35
|
5,39
|
6,58
|
7,85
|
9,19
|
10,6
|
|
0,05
|
1
|
1,39
|
1,88
|
2,49
|
3,24
|
4,09
|
5,04
|
6,08
|
7,21
|
8,40
|
9,65
|
|
0,1
|
1
|
1,36
|
1,81
|
2,35
|
3,01
|
3,74
|
4,56
|
5,44
|
6,38
|
7,37
|
8,41
|
|
0,3
|
1
|
1,31
|
1,69
|
2,12
|
2,65
|
3,21
|
3,82
|
4,48
|
5,17
|
5,88
|
6,61
|
|
0,5
|
1
|
1,28
|
1,63
|
2,03
|
2,48
|
2,97
|
3,50
|
4,06
|
4,64
|
5,24
|
5,84
|
|
1
|
1
|
1,25
|
1,55
|
1,90
|
2,26
|
2,66
|
3,07
|
3,5
|
3,96
|
4,41
|
4,87
|
|
3
|
1
|
1,20
|
1,42
|
1,66
|
1,91
|
2,17
|
2,43
|
2,69
|
2,95
|
3,21
|
3,47
|
|
5
|
1
|
1,17
|
1,36
|
1,55
|
1,75
|
1,95
|
2,14
|
2,34
|
2,52
|
2,70
|
2,88
|
|
10
|
1
|
1,13
|
1,26
|
1,40
|
1,52
|
1,65
|
1,76
|
1,87
|
1,97
|
2,06
|
2,15
|
|
20
|
1
|
1,08
|
1,16
|
1,23
|
1,29
|
1,34
|
1,38
|
1,42
|
1,45
|
1,47
|
1,49
|
|
25
|
1
|
1,07
|
1,12
|
1,17
|
1,21
|
1,24
|
1,26
|
1,28
|
1,28
|
1,29
|
1,29
|
|
30
|
1
|
1,05
|
1,09
|
1,12
|
1,14
|
1,15
|
1,16
|
1,16
|
1,15
|
1,14
|
1,13
|
|
40
|
1
|
1,02
|
1,03
|
1,03
|
1,03
|
1,01
|
0,995
|
0,972
|
0,946
|
0,915
|
0,883
|
|
50
|
1
|
0,997
|
0,981
|
0,959
|
0,93
|
0,898
|
0,862
|
0,823
|
0,783
|
0,741
|
0,699
|
|
60
|
1
|
0,972
|
0,993
|
0,890
|
0,843
|
0,794
|
0,745
|
0,695
|
0,646
|
0,597
|
0,549
|
|
70
|
1
|
0,945
|
0,884
|
0,822
|
0,758
|
0,696
|
0,636
|
0,578
|
0,523
|
0,471
|
0,422
|
|
75
|
1
|
0,931
|
0,858
|
0,786
|
0,715
|
0,647
|
0,583
|
0,522
|
0,465
|
0,412
|
0,363
|
|
80
|
1
|
0,915
|
0,830
|
0,748
|
0,669
|
0,596
|
0,528
|
0,465
|
0,407
|
0,354
|
0,306
|
|
90
|
1
|
0,876
|
0,761
|
0,656
|
0,563
|
0,479
|
0,406
|
0,341
|
0,284
|
0,235
|
0,193
|
|
95
|
1
|
0,844
|
0,708
|
0,588
|
0,487
|
0,400
|
0,326
|
0,263
|
0,210
|
0,166
|
0,129
|
|
97
|
1
|
0,825
|
0,675
|
0,548
|
0,443
|
0,355
|
0,282
|
0,221
|
0,171
|
0,131
|
0,099
|
|
99
|
1
|
0,486
|
0,618
|
0,484
|
0,369
|
0,283
|
0,213
|
0,158
|
0,116
|
0,083
|
0,058
|
|
99,5
|
1
|
0,769
|
0,588
|
0,446
|
0,334
|
0,249
|
0,182
|
0,131
|
0,092
|
0,064
|
0,043
|
|
99,7
|
1
|
0,756
|
0,568
|
0,422
|
0,312
|
0,228
|
0,163
|
0,114
|
0,079
|
0,053
|
0,034
|
|
99,9
|
1
|
0,732
|
0,531
|
0,381
|
0,273
|
0,192
|
0,131
|
0,088
|
0,057
|
0,036
|
0,022
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|
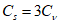
|
||||||||||
|
0,001
|
21,3
|
24,5
|
27,9
|
31,5
|
35,3
|
39,3
|
43,4
|
47,8
|
52,5
|
57,4
|
|
0,01
|
14,8
|
16,8
|
19,0
|
21,2
|
23,5
|
25,9
|
28,4
|
31,0
|
33,7
|
36,5
|
|
0,03
|
12,1
|
13,7
|
15,3
|
17,0
|
18,8
|
20,6
|
22,4
|
24,3
|
26,3
|
28,4
|
|
0,05
|
11,0
|
12,4
|
13,8
|
15,2
|
16,8
|
18,3
|
19,9
|
21,5
|
23,3
|
25,1
|
|
0,1
|
9,49
|
10,6
|
11,8
|
13,0
|
14,2
|
15,4
|
16,7
|
18,0
|
19,4
|
20,8
|
|
0,3
|
7,37
|
8,15
|
8,94
|
9,75
|
10,6
|
11,4
|
12,3
|
13,1
|
14,0
|
14,8
|
|
0,5
|
6,47
|
7,10
|
7,75
|
8,41
|
9,07
|
9,74
|
10,4
|
11,1
|
11,8
|
12,4
|
|
1
|
5,33
|
5,79
|
6,26
|
6,74
|
7,21
|
7,68
|
8,14
|
8,61
|
9,07
|
9,53
|
|
3
|
3,73
|
3,98
|
4,20
|
4,44
|
4,67
|
4,89
|
5,10
|
5,31
|
5,51
|
5,7
|
|
5
|
3,05
|
3,22
|
3,37
|
3,52
|
3,66
|
3,80
|
3,92
|
4,04
|
4,15
|
4,26
|
|
10
|
2,23
|
2,30
|
2,36
|
2,42
|
2,47
|
2,51
|
2,55
|
2,58
|
2,60
|
2,62
|
|
20
|
1,50
|
1,50
|
1,50
|
1,49
|
1,48
|
1,46
|
1,45
|
1,42
|
1,40
|
1,37
|
|
25
|
1,28
|
1,27
|
1,25
|
1,23
|
1,20
|
1,18
|
1,15
|
1,12
|
1,08
|
1,05
|
|
30
|
1,11
|
1,08
|
1,06
|
1,03
|
0,997
|
0,964
|
0,929
|
0,892
|
0,855
|
0,818
|
|
40
|
0,848
|
0,812
|
0,775
|
0,736
|
0,697
|
0,659
|
0,620
|
0,581
|
0,544
|
0,507
|
|
50
|
0,656
|
0,614
|
0,572
|
0,531
|
0,491
|
0,452
|
0,415
|
0,379
|
0,345
|
0,313
|
|
60
|
0,503
|
0,459
|
0,417
|
0,377
|
0,339
|
0,304
|
0,271
|
0,240
|
0,212
|
0,186
|
|
70
|
0,375
|
0,333
|
0,293
|
0,257
|
0,224
|
0,194
|
0,166
|
0,142
|
0,121
|
0,102
|
|
75
|
0,318
|
0,277
|
0,239
|
0,206
|
0,176
|
0,149
|
0,125
|
0,105
|
0,087
|
0,071
|
|
80
|
0,263
|
0,224
|
0,190
|
0,160
|
0,133
|
0,110
|
0,090
|
0,073
|
0,059
|
0,047
|
|
90
|
0,156
|
0,126
|
0,100
|
0,078
|
0,061
|
0,047
|
0,035
|
0,026
|
0,019
|
0,014
|
|
95
|
0,100
|
0,076
|
0,057
|
0,042
|
0,030
|
0,022
|
0,015
|
0,010
|
0,007
|
0,004
|
|
97
|
0,073
|
0,054
|
0,038
|
0,027
|
0,018
|
0,012
|
0,008
|
0,005
|
0,003
|
0,002
|
|
99
|
0,040
|
0,027
|
0,017
|
0,011
|
0,007
|
0,004
|
0,002
|
0,001
|
0,001
|
4·10
-4
|
|
99,5
|
0,028
|
0,018
|
0,011
|
0,006
|
0,004
|
0,002
|
0,001
|
6·10
-4
|
3·10
-4
|
1·10
-4
|
|
99,7
|
0,022
|
0,014
|
0,008
|
0,004
|
0,002
|
0,001
|
6·10
-4
|
3·10
-4
|
1·10
-4
|
6·10
-5
|
|
99,9
|
0,013
|
0,007
|
0,004
|
0,002
|
0,001
|
4·10
-4
|
2·10
-4
|
8·10
-5
|
3·10
-5
|
1·10
-5
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
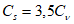
|
||||||||||
|
0,001
|
1,56
|
2,39
|
3,59
|
5,23
|
7,26
|
9,65
|
12,3
|
15,2
|
18,2
|
21,6
|
|
0,01
|
1,48
|
2,12
|
2,99
|
4,12
|
5,46
|
6,94
|
8,6
|
10,4
|
12,3
|
14,4
|
|
0,03
|
1,43
|
1,98
|
2,71
|
3,63
|
4,64
|
5,85
|
7,17
|
8,56
|
10,0
|
11,6
|
|
0,05
|
1,4
|
1,93
|
2,58
|
3,41
|
4,33
|
5,38
|
6,54
|
7,77
|
9,04
|
10,4
|
|
0,1
|
1,37
|
1,84
|
2,43
|
3,14
|
3,93
|
4,79
|
5,75
|
6,77
|
7,82
|
8,90
|
|
0,3
|
1,31
|
1,71
|
2,16
|
2,75
|
3,36
|
4,00
|
4,67
|
5,36
|
6,08
|
6,83
|
|
0,5
|
1,29
|
1,65
|
2,07
|
2,55
|
3,06
|
3,62
|
4,18
|
4,76
|
5,35
|
5,97
|
|
1
|
1,25
|
1,57
|
1,93
|
2,31
|
2,71
|
3,13
|
3,56
|
4,00
|
4,45
|
4,90
|
|
3
|
1,20
|
1,43
|
1,68
|
1,93
|
2,18
|
2,43
|
2,68
|
2,94
|
3,19
|
3,43
|
|
5
|
1,17
|
1,36
|
1,56
|
1,75
|
1,94
|
2,13
|
2,31
|
2,49
|
2,66
|
2,83
|
|
10
|
1,13
|
1,26
|
1,39
|
1,52
|
1,63
|
1,74
|
1,84
|
1,93
|
2,02
|
2,10
|
|
20
|
1,08
|
1,16
|
1,22
|
1,28
|
1,32
|
1,36
|
1,39
|
1,42
|
1,44
|
1,45
|
|
25
|
1,07
|
1,12
|
1,16
|
1,20
|
1,22
|
1,24
|
1,25
|
1,26
|
1,26
|
1,26
|
|
30
|
1,05
|
1,08
|
1,11
|
1,13
|
1,14
|
1,14
|
1,14
|
1,13
|
1,12
|
1,11
|
|
40
|
1,02
|
1,03
|
1,03
|
1,02
|
1,00
|
0,984
|
0,96
|
0,935
|
0,907
|
0,877
|
|
50
|
0,997
|
0,978
|
0,954
|
0,925
|
0,892
|
0,856
|
0,819
|
0,781
|
0,742
|
0,703
|
|
60
|
0,972
|
0,931
|
0,887
|
0,841
|
0,793
|
0,745
|
0,698
|
0,652
|
0,606
|
0,562
|
|
70
|
0,945
|
0,883
|
0,821
|
0,760
|
0,700
|
0,643
|
0,588
|
0,537
|
0,488
|
0,442
|
|
75
|
0,931
|
0,858
|
0,787
|
0,719
|
0,654
|
0,593
|
0,536
|
0,482
|
0,432
|
0,386
|
|
80
|
0,915
|
0,831
|
0,751
|
0,676
|
0,606
|
0,541
|
0,482
|
0,427
|
0,377
|
0,332
|
|
90
|
0,877
|
0,764
|
0,664
|
0,576
|
0,496
|
0,427
|
0,366
|
0,311
|
0,263
|
0,221
|
|
95
|
0,840
|
0,713
|
0,600
|
0,504
|
0,422
|
0,351
|
0,290
|
0,239
|
0,195
|
0,158
|
|
97
|
0,827
|
0,683
|
0,563
|
0,463
|
0,380
|
0,309
|
0,249
|
0,201
|
0,160
|
0,126
|
|
99
|
0,788
|
0,629
|
0,499
|
0,396
|
0,312
|
0,244
|
0,186
|
0,145
|
0,110
|
0,082
|
|
99,5
|
0,773
|
0,601
|
0,467
|
0,362
|
0,280
|
0,214
|
0,160
|
0,121
|
0,089
|
0,064
|
|
99,7
|
0,759
|
0,582
|
0,446
|
0,341
|
0,260
|
0,196
|
0,146
|
0,106
|
0,077
|
0,054
|
|
99,9
|
0,737
|
0,548
|
0,408
|
0,303
|
0,224
|
0,165
|
0,118
|
0,083
|
0,057
|
0,039
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|
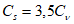
|
||||||||||
|
0,001
|
25,1
|
28,9
|
32,8
|
36,9
|
41,2
|
45,7
|
50,3
|
55,1
|
60,1
|
65,4
|
|
0,01
|
16,5
|
18,8
|
21,1
|
23,5
|
26,0
|
28,6
|
31,3
|
34,0
|
36,8
|
39,9
|
|
0,03
|
13,2
|
14,8
|
16,6
|
18,4
|
20,2
|
22,1
|
24,1
|
26,1
|
28,1
|
30,2
|
|
0,05
|
11,8
|
13,2
|
14,7
|
16,3
|
17,8
|
19,4
|
21,1
|
22,8
|
24,5
|
26,2
|
|
0,1
|
10,0
|
11,2
|
12,4
|
13,6
|
14,9
|
16,1
|
17,4
|
18,8
|
20,1
|
21,4
|
|
0,3
|
7,59
|
8,37
|
9,17
|
9,97
|
10,8
|
11,6
|
12,4
|
13,3
|
14,1
|
15,0
|
|
0,5
|
6,59
|
7,22
|
7,86
|
8,50
|
9,14
|
9,79
|
10,4
|
11,1
|
11,8
|
12,4
|
|
1
|
5,36
|
5,80
|
6,26
|
6,71
|
7,16
|
7,61
|
8,05
|
8,49
|
8,92
|
9,36
|
|
3
|
3,67
|
3,90
|
4,12
|
4,34
|
4,55
|
4,75
|
4,95
|
5,14
|
5,32
|
5,50
|
|
5
|
2,98
|
3,14
|
3,28
|
3,42
|
3,55
|
3,67
|
3,78
|
3,89
|
3,99
|
4,08
|
|
10
|
2,17
|
2,23
|
2,29
|
2,34
|
2,38
|
2,42
|
2,46
|
2,48
|
2,51
|
2,52
|
|
20
|
1,46
|
1,46
|
1,46
|
1,45
|
1,44
|
1,43
|
1,41
|
1,39
|
1,37
|
1,35
|
|
25
|
1,25
|
1,24
|
1,22
|
1,21
|
1,18
|
1,16
|
1,14
|
1,11
|
0,108
|
1,05
|
|
30
|
1,09
|
1,07
|
1,04
|
1,02
|
0,989
|
0,96
|
0,929
|
0,897
|
0,864
|
0,831
|
|
40
|
0,845
|
0,812
|
0,777
|
0,743
|
0,708
|
0,673
|
0,638
|
0,604
|
0,570
|
0,537
|
|
50
|
0,664
|
0,625
|
0,587
|
0,549
|
0,513
|
0,477
|
0,443
|
0,410
|
0,379
|
0,350
|
|
60
|
0,520
|
0,479
|
0,440
|
0,403
|
0,368
|
0,335
|
0,303
|
0,274
|
0,247
|
0,222
|
|
70
|
0,398
|
0,358
|
0,321
|
0,286
|
0,254
|
0,225
|
0,199
|
0,175
|
0,153
|
0,134
|
|
75
|
0,343
|
0,304
|
0,268
|
0,236
|
0,206
|
0,180
|
0,156
|
0,135
|
0,116
|
0,099
|
|
80
|
0,290
|
0,253
|
0,219
|
0,189
|
0,163
|
0,139
|
0,118
|
0,100
|
0,084
|
0,070
|
|
90
|
0,185
|
0,154
|
0,127
|
0,104
|
0,085
|
0,069
|
0,055
|
0,044
|
0,035
|
0,027
|
|
95
|
0,127
|
0,101
|
0,080
|
0,062
|
0,048
|
0,037
|
0,028
|
0,021
|
0,016
|
0,011
|
|
97
|
0,098
|
0,076
|
0,058
|
0,044
|
0,033
|
0,024
|
0,018
|
0,013
|
0,009
|
0,006
|
|
99
|
0,061
|
0,044
|
0,032
|
0,022
|
0,016
|
0,011
|
0,007
|
0,005
|
0,003
|
0,002
|
|
99,5
|
0,046
|
0,032
|
0,022
|
0,015
|
0,010
|
0,006
|
0,004
|
0,003
|
0,002
|
0,001
|
|
99,7
|
0,038
|
0,026
|
0,017
|
0,011
|
0,007
|
0,004
|
0,003
|
0,002
|
0,001
|
0,5·10
-3
|
|
99,9
|
0,026
|
0,016
|
0,010
|
0,006
|
0,004
|
0,002
|
0,001
|
0,001
|
0,3·10
-3
|
0,2·10
-3
|
|
P
, %
|
|
||||||||||
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|

|
|||||||||||
|
0,001
|
0
|
1,59
|
2,49
|
3,90
|
5,80
|
8,50
|
10,9
|
13,9
|
17,2
|
20,8
|
24,6
|
|
0,01
|
0
|
1,50
|
2,18
|
3,17
|
4,43
|
5,91
|
7,58
|
9,41
|
11,4
|
13,4
|
15,5
|
|
0,03
|
0
|
1,44
|
2,04
|
2,86
|
3,86
|
5,02
|
6,3
|
7,67
|
9,14
|
10,7
|
12,3
|
|
0,05
|
0
|
1,41
|
1,97
|
2,72
|
3,61
|
4,63
|
5,76
|
6,96
|
8,22
|
9,56
|
11,0
|
|
0,1
|
0
|
1,38
|
1,88
|
2,53
|
3,29
|
4,15
|
5,07
|
6,05
|
7,08
|
8,15
|
9,26
|
|
0,3
|
0
|
1,32
|
1,74
|
2,24
|
2,82
|
3,44
|
4,09
|
4,79
|
5,50
|
6,22
|
6,96
|
|
0,5
|
0
|
1,29
|
1,67
|
2,12
|
2,61
|
3,13
|
3,68
|
4,26
|
4,85
|
5,43
|
6,03
|
|
1
|
0
|
1,25
|
1,58
|
1,94
|
2,31
|
2,75
|
3,17
|
3,59
|
4,03
|
4,47
|
4,91
|
|
3
|
0
|
1,20
|
1,44
|
1,68
|
1,93
|
2,18
|
2,43
|
2,68
|
2,92
|
3,16
|
3,39
|
|
5
|
0
|
1,17
|
1,36
|
1,56
|
1,75
|
1,94
|
2,12
|
2,29
|
2,46
|
2,62
|
2,78
|
|
10
|
0
|
1,13
|
1,26
|
1,39
|
1,51
|
1,62
|
1,72
|
1,81
|
1,90
|
1,98
|
2,05
|
|
20
|
0
|
1,08
|
1,15
|
1,22
|
1,27
|
1,31
|
1,34
|
1,37
|
1,40
|
1,41
|
1,42
|
|
25
|
0
|
1,07
|
1,12
|
1,16
|
1,19
|
1,21
|
1,23
|
1,24
|
1,24
|
1,24
|
1,24
|
|
30
|
0
|
1,05
|
1,08
|
1,11
|
1,12
|
1,13
|
1,13
|
1,13
|
1,12
|
1,11
|
1,10
|
|
40
|
0
|
1,02
|
1,02
|
1,02
|
1,01
|
0,996
|
0,976
|
0,954
|
0,929
|
0,902
|
0,873
|
|
50
|
0
|
0,997
|
0,976
|
0,950
|
0,920
|
0,888
|
0,853
|
0,818
|
0,781
|
0,744
|
0,707
|
|
60
|
0
|
0,972
|
0,929
|
0,885
|
0,839
|
0,793
|
0,747
|
0,702
|
0,658
|
0,614
|
0,572
|
|
70
|
0
|
0,945
|
0,883
|
0,821
|
0,761
|
0,704
|
0,649
|
0,597
|
0,548
|
0,501
|
0,457
|
|
75
|
0
|
0,931
|
0,858
|
0,788
|
0,722
|
0,660
|
0,601
|
0,546
|
0,495
|
0,448
|
0,403
|
|
80
|
0
|
0,915
|
0,832
|
0,754
|
0,681
|
0,614
|
0,553
|
0,496
|
0,443
|
0,395
|
0,351
|
|
90
|
0
|
0,877
|
0,767
|
0,671
|
0,586
|
0,511
|
0,444
|
0,384
|
0,331
|
0,284
|
0,243
|
|
95
|
0
|
0,846
|
0,719
|
0,611
|
0,519
|
0,440
|
0,372
|
0,312
|
0,261
|
0,217
|
0,180
|
|
97
|
0
|
0,829
|
0,690
|
0,576
|
0,481
|
0,400
|
0,332
|
0,274
|
0,224
|
0,182
|
0,147
|
|
99
|
0
|
0,790
|
0,638
|
0,516
|
0,417
|
0,336
|
0,269
|
0,214
|
0,168
|
0,132
|
0,102
|
|
99,5
|
0
|
0,776
|
0,612
|
0,485
|
0,386
|
0,035
|
0,239
|
0,186
|
0,144
|
0,110
|
0,083
|
|
99,7
|
0
|
0,762
|
0,594
|
0,466
|
0,366
|
0,286
|
0,221
|
0,170
|
0,129
|
0,097
|
0,072
|
|
99,9
|
0
|
0,742
|
0,561
|
0,43
|
0,331
|
0,252
|
0,189
|
0,141
|
0,104
|
0,075
|
0,054
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2
|
|

|
||||||||||
|
0,001
|
28,6
|
32,8
|
37,2
|
41,8
|
46,6
|
51,5
|
56,6
|
61,8
|
67,2
|
72,8
|
|
0,01
|
17,9
|
20,3
|
22,8
|
25,4
|
28,0
|
30,8
|
33,6
|
36,5
|
39,4
|
42,4
|
|
0,03
|
14,0
|
15,8
|
17,6
|
19,4
|
21,3
|
23,3
|
25,3
|
27,3
|
29,4
|
31,5
|
|
0,05
|
12,4
|
13,9
|
15,4
|
17,0
|
18,6
|
20,3
|
21,9
|
23,7
|
25,4
|
27,2
|
|
0,1
|
10,4
|
11,6
|
12,8
|
14,0
|
15,3
|
16,6
|
17,9
|
19,2
|
20,6
|
21,9
|
|
0,3
|
7,73
|
8,53
|
9,31
|
10,1
|
10,9
|
11,7
|
12,5
|
13,3
|
14,2
|
15,0
|
|
0,5
|
6,65
|
7,29
|
7,91
|
8,53
|
9,16
|
9,79
|
10,4
|
11,0
|
11,7
|
12,3
|
|
1
|
5,34
|
5,79
|
6,22
|
6,66
|
7,09
|
7,52
|
7,95
|
8,37
|
8,78
|
9,19
|
|
3
|
3,62
|
3,83
|
4,04
|
4,25
|
4,45
|
4,64
|
4,83
|
5,01
|
5,18
|
5,34
|
|
5
|
2,93
|
3,07
|
3,21
|
3,34
|
3,46
|
3,57
|
3,68
|
3,78
|
3,87
|
3,96
|
|
10
|
2,12
|
2,18
|
2,24
|
2,28
|
2,32
|
2,36
|
2,39
|
2,42
|
2,44
|
2,45
|
|
20
|
1,43
|
1,44
|
1,43
|
1,43
|
1,42
|
1,41
|
1,39
|
1,38
|
1,36
|
1,33
|
|
25
|
1,23
|
1,22
|
1,21
|
1,19
|
1,17
|
1,15
|
1,13
|
1,1
|
1,08
|
1,05
|
|
30
|
1,08
|
1,06
|
1,04
|
1,01
|
0,985
|
0,958
|
0,929
|
0,90
|
0,871
|
0,841
|
|
40
|
0,843
|
0,812
|
0,781
|
0,748
|
0,716
|
0,684
|
0,652
|
0,62
|
0,588
|
0,558
|
|
50
|
0,670
|
0,634
|
0,598
|
0,562
|
0,529
|
0,495
|
0,464
|
0,433
|
0,403
|
0,375
|
|
60
|
0,532
|
0,494
|
0,457
|
0,421
|
0,388
|
0,356
|
0,327
|
0,299
|
0,273
|
0,249
|
|
70
|
0,416
|
0,377
|
0,341
|
0,308
|
0,277
|
0,248
|
0,223
|
0,199
|
0,177
|
0,157
|
|
75
|
0,362
|
0,325
|
0,29
|
0,258
|
0,230
|
0,203
|
0,179
|
0,158
|
0,139
|
0,121
|
|
80
|
0,311
|
0,274
|
0,242
|
0,212
|
0,185
|
0,162
|
0,140
|
0,122
|
0,105
|
0,090
|
|
90
|
0,207
|
0,176
|
0,148
|
0,125
|
0,104
|
0,087
|
0,072
|
0,060
|
0,049
|
0,040
|
|
95
|
0,148
|
0,121
|
0,098
|
0,08
|
0,064
|
0,051
|
0,041
|
0,032
|
0,025
|
0,019
|
|
97
|
0,119
|
0,095
|
0,075
|
0,059
|
0,046
|
0,036
|
0,028
|
0,021
|
0,016
|
0,012
|
|
99
|
0,078
|
0,06
|
0,045
|
0,034
|
0,025
|
0,018
|
0,013
|
0,009
|
0,006
|
0,004
|
|
99,5
|
0,062
|
0,046
|
0,034
|
0,024
|
0,017
|
0,012
|
0,008
|
0,006
|
0,004
|
0,003
|
|
99,7
|
0,053
|
0,038
|
0,027
|
0,019
|
0,013
|
0,009
|
0,006
|
0,004
|
0,003
|
0,002
|
|
99,9
|
0,038
|
0,026
|
0,018
|
0,012
|
0,008
|
0,005
|
0,003
|
0,002
|
0,001
|
0,001
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
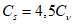
|
||||||||||
|
0,01
|
1,48
|
2,26
|
3,53
|
4,74
|
6,36
|
8,15
|
10,1
|
12,2
|
14,4
|
16,7
|
|
0,03
|
1,44
|
2,09
|
2,98
|
4,07
|
5,30
|
6,65
|
8,09
|
9,62
|
11,2
|
12,9
|
|
0,05
|
1,41
|
2,02
|
2,82
|
3,78
|
4,86
|
6,03
|
7,27
|
8,58
|
9,95
|
11,4
|
|
0,1
|
1,38
|
1,92
|
2,61
|
3,41
|
4,30
|
5,25
|
6,26
|
7,31
|
8,40
|
9,53
|
|
0,3
|
1,33
|
1,76
|
2,29
|
2,88
|
3,52
|
4,18
|
4,87
|
5,58
|
6,31
|
7,06
|
|
0,5
|
1,30
|
1,69
|
2,15
|
2,66
|
3,19
|
3,74
|
4,31
|
4,89
|
5,48
|
6,08
|
|
1
|
1,27
|
1,59
|
1,97
|
2,36
|
2,77
|
3,19
|
3,61
|
4,04
|
4,47
|
4,90
|
|
3
|
1,21
|
1,44
|
1,69
|
1,93
|
2,18
|
2,42
|
2,66
|
2,90
|
3,12
|
3,35
|
|
5
|
1,18
|
1,37
|
1,56
|
1,75
|
1,93
|
2,10
|
2,27
|
2,44
|
2,59
|
2,74
|
|
10
|
1,13
|
1,26
|
1,39
|
1,50
|
1,60
|
1,70
|
1,79
|
1,88
|
1,95
|
2,02
|
|
20
|
1,08
|
1,15
|
1,21
|
1,26
|
1,30
|
1,33
|
1,36
|
1,38
|
1,40
|
1,41
|
|
25
|
1,06
|
1,11
|
1,15
|
1,18
|
1,20
|
1,21
|
1,22
|
1,23
|
1,23
|
1,23
|
|
30
|
1,05
|
1,08
|
1,10
|
1,11
|
1,12
|
1,12
|
1,12
|
1,11
|
1,10
|
1,09
|
|
40
|
1,02
|
1,02
|
1,02
|
1,01
|
0,989
|
0,97
|
0,949
|
0,925
|
0,899
|
0,871
|
|
50
|
0,993
|
0,974
|
0,947
|
0,917
|
0,885
|
0,851
|
0,817
|
0,782
|
0,746
|
0,711
|
|
60
|
0,968
|
0,928
|
0,883
|
0,838
|
0,793
|
0,749
|
0,705
|
0,663
|
0,621
|
0,581
|
|
70
|
0,943
|
0,882
|
0,822
|
0,763
|
0,708
|
0,655
|
0,605
|
0,557
|
0,512
|
0,469
|
|
75
|
0,93
|
0,858
|
0,79
|
0,726
|
0,666
|
0,609
|
0,556
|
0,506
|
0,46
|
0,417
|
|
80
|
0,915
|
0,833
|
0,757
|
0,687
|
0,622
|
0,562
|
0,507
|
0,456
|
0,409
|
0,366
|
|
90
|
0,878
|
0,771
|
0,677
|
0,596
|
0,523
|
0,458
|
0,399
|
0,347
|
0,301
|
0,260
|
|
95
|
0,848
|
0,724
|
0,620
|
0,532
|
0,455
|
0,388
|
0,33
|
0,279
|
0,235
|
0,197
|
|
97
|
0,831
|
0,696
|
0,587
|
0,495
|
0,417
|
0,350
|
0,292
|
0,242
|
0,200
|
0,165
|
|
99
|
0,798
|
0,648
|
0,530
|
0,435
|
0,355
|
0,289
|
0,233
|
0,187
|
0,149
|
0,118
|
|
99,5
|
0,781
|
0,622
|
0,502
|
0,405
|
0,326
|
0,26
|
0,206
|
0,162
|
0,127
|
0,098
|
|
99,7
|
0,769
|
0,606
|
0,483
|
0,386
|
0,307
|
0,242
|
0,19
|
0,147
|
0,113
|
0,086
|
|
99,9
|
0,746
|
0,575
|
0,449
|
0,352
|
0,274
|
0,211
|
0,161
|
0,122
|
0,091
|
0,067
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
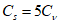
|
||||||||||
|
0,001
|
1,67
|
2,75
|
4,38
|
6,87
|
9,90
|
13,4
|
17,1
|
21,2
|
25,3
|
|
|
0,01
|
1,54
|
2,34
|
3,43
|
4,91
|
6,65
|
8,70
|
10,7
|
12,7
|
15,1
|
17,5
|
|
0,03
|
1,47
|
2,15
|
3,07
|
4,23
|
5,50
|
6,95
|
8,43
|
9,96
|
11,6
|
13,4
|
|
0,05
|
1,43
|
2,06
|
2,87
|
3,90
|
5,05
|
6,24
|
7,51
|
8,82
|
10,3
|
11,7
|
|
0,1
|
1,40
|
1,95
|
2,66
|
3,51
|
4,44
|
5,40
|
6,43
|
7,54
|
8,64
|
9,73
|
|
0,3
|
1,34
|
1,78
|
2,31
|
2,92
|
3,52
|
4,22
|
4,91
|
5,69
|
6,41
|
7,12
|
|
0,5
|
1,31
|
1,70
|
2,16
|
2,69
|
3,21
|
3,77
|
4,34
|
4,93
|
5,52
|
6,10
|
|
1
|
1,27
|
1,61
|
1,98
|
2,38
|
2,79
|
3,21
|
3,65
|
4,06
|
4,50
|
4,89
|
|
3
|
1,20
|
1,44
|
1,67
|
1,93
|
2,17
|
2,42
|
2,62
|
2,88
|
3,10
|
3,32
|
|
5
|
1,17
|
1,36
|
1,55
|
1,74
|
1,90
|
2,08
|
2,22
|
2,41
|
2,54
|
2,71
|
|
10
|
1,13
|
1,26
|
1,37
|
1,49
|
1,60
|
1,70
|
1,79
|
1,86
|
1,94
|
2,00
|
|
20
|
1,08
|
1,15
|
1,21
|
1,25
|
1,30
|
1,32
|
1,34
|
1,36
|
1,36
|
1,39
|
|
25
|
1,06
|
1,11
|
1,15
|
1,17
|
1,20
|
1,20
|
1,20
|
1,22
|
1,22
|
1,12
|
|
30
|
1,05
|
1,08
|
1,09
|
1,10
|
1,10
|
1,11
|
1,10
|
1,10
|
1,09
|
1,08
|
|
40
|
1,02
|
1,02
|
1,01
|
1,00
|
0,98
|
0,97
|
0,94
|
0,92
|
0,90
|
0,87
|
|
50
|
0,99
|
0,97
|
0,94
|
0,92
|
0,88
|
0,85
|
0,82
|
0,78
|
0,75
|
0,714
|
|
60
|
0,97
|
0,93
|
0,88
|
0,84
|
0,79
|
0,75
|
0,71
|
0,67
|
0,63
|
0,588
|
|
70
|
0,94
|
0,88
|
0,82
|
0,77
|
0,71
|
0,66
|
0,61
|
0,56
|
0,52
|
0,479
|
|
75
|
0,93
|
0,86
|
0,79
|
0,73
|
0,67
|
0,62
|
0,56
|
0,51
|
0,47
|
0,428
|
|
80
|
0,91
|
0,83
|
0,75
|
0,69
|
0,63
|
0,57
|
0,52
|
0,47
|
0,42
|
0,378
|
|
90
|
0,88
|
0,77
|
0,68
|
0,61
|
0,53
|
0,47
|
0,41
|
0,36
|
0,32
|
0,274
|
|
95
|
0,84
|
0,73
|
0,63
|
0,55
|
0,47
|
0,40
|
0,34
|
0,29
|
0,25
|
0,211
|
|
97
|
0,82
|
0,70
|
0,6
|
0,51
|
0,43
|
0,36
|
0,31
|
0,26
|
0,22
|
0,178
|
|
99
|
0,78
|
0,66
|
0,55
|
0,45
|
0,37
|
0,31
|
0,25
|
0,20
|
0,16
|
0,131
|
|
99,5
|
0,76
|
0,63
|
0,52
|
0,42
|
0,34
|
0,28
|
0,23
|
0,18
|
0,14
|
0,110
|
|
99,7
|
0,75
|
0,62
|
0,51
|
0,41
|
0,32
|
0,26
|
0,21
|
0,16
|
0,12
|
0,098
|
|
99,9
|
0,73
|
0,59
|
0,47
|
0,37
|
0,29
|
0,23
|
0,18
|
0,14
|
0,1
|
0,078
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
|
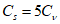
|
||||||||||
|
0,01
|
20
|
22,6
|
25,4
|
28,3
|
31,2
|
34,1
|
37,1
|
40,1
|
43,2
|
46,3
|
|
0,03
|
15,1
|
17,0
|
18,8
|
20,9
|
22,8
|
24,8
|
26,9
|
29,0
|
31,1
|
33,3
|
|
0,05
|
13,2
|
14,7
|
16,3
|
18,0
|
19,6
|
21,3
|
23,0
|
24,7
|
26,5
|
28,3
|
|
0,1
|
10,9
|
12,1
|
13,3
|
14,6
|
15,8
|
17,1
|
18,4
|
19,7
|
21,0
|
22,4
|
|
0,3
|
7,87
|
8,63
|
9,40
|
10,2
|
11,0
|
11,7
|
12,5
|
13,3
|
14,1
|
14,9
|
|
0,5
|
6,70
|
7,30
|
7,90
|
8,50
|
9,12
|
9,71
|
10,3
|
10,9
|
11,6
|
12,1
|
|
1
|
5,31
|
5,73
|
6,14
|
6,54
|
6,97
|
7,37
|
7,77
|
8,16
|
8,54
|
8,92
|
|
3
|
3,53
|
3,73
|
3,93
|
4,10
|
4,30
|
4,48
|
4,65
|
4,61
|
4,97
|
5,12
|
|
5
|
2,85
|
2,98
|
3,10
|
3,21
|
3,33
|
3,44
|
3,53
|
3,62
|
3,71
|
3,79
|
|
10
|
2,06
|
2,11
|
2,16
|
2,20
|
2,24
|
2,28
|
2,31
|
2,33
|
2,35
|
2,36
|
|
20
|
1,40
|
1,40
|
1,40
|
1,39
|
1,39
|
1,38
|
1,37
|
1,35
|
1,33
|
1,32
|
|
25
|
1,21
|
1,20
|
1,19
|
1,17
|
1,16
|
1,14
|
1,12
|
1,10
|
1,07
|
1,05
|
|
30
|
1,06
|
1,04
|
1,03
|
1,00
|
0,981
|
0,957
|
0,932
|
0,906
|
0,88
|
0,854
|
|
40
|
0,843
|
0,815
|
0,786
|
0,758
|
0,728
|
0,699
|
0,670
|
0,641
|
0,613
|
0,586
|
|
50
|
0,680
|
0,647
|
0,614
|
0,584
|
0,551
|
0,520
|
0,491
|
0,463
|
0,435
|
0,409
|
|
60
|
0,550
|
0,514
|
0,480
|
0,450
|
0,416
|
0,387
|
0,359
|
0,323
|
0,308
|
0,284
|
|
70
|
0,440
|
0,403
|
0,369
|
0,341
|
0,303
|
0,281
|
0,256
|
0,232
|
0,211
|
0,191
|
|
75
|
0,389
|
0,353
|
0,319
|
0,292
|
0,261
|
0,235
|
0,212
|
0,19
|
0,171
|
0,153
|
|
80
|
0,339
|
0,304
|
0,272
|
0,246
|
0,217
|
0,193
|
0,171
|
0,152
|
0,135
|
0,119
|
|
90
|
0,238
|
0,206
|
0,178
|
0,157
|
0,133
|
0,114
|
0,098
|
0,084
|
0,071
|
0,061
|
|
95
|
0,178
|
0,150
|
0,126
|
0,109
|
0,088
|
0,073
|
0,061
|
0,05
|
0,042
|
0,034
|
|
97
|
0,148
|
0,122
|
0,101
|
0,085
|
0,068
|
0,055
|
0,045
|
0,036
|
0,029
|
0,023
|
|
99
|
0,105
|
0,083
|
0,066
|
0,054
|
0,041
|
0,032
|
0,025
|
0,019
|
0,015
|
0,011
|
|
99,5
|
0,087
|
0,067
|
0,052
|
0,042
|
0,031
|
0,023
|
0,018
|
0,013
|
0,01
|
0,007
|
|
99,7
|
0,076
|
0,058
|
0,044
|
0,035
|
0,025
|
0,019
|
0,014
|
0,01
|
0,008
|
0,006
|
|
99,9
|
0,059
|
0,044
|
0,032
|
0,025
|
0,017
|
0,012
|
0,009
|
0,006
|
0,004
|
0,003
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
|
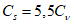
|
||||||||||
|
0,01
|
1,52
|
2,41
|
3,7
|
5,3
|
7,12
|
9,1
|
11,2
|
13,4
|
15,8
|
18,2
|
|
0,03
|
1,46
|
2,20
|
3,22
|
4,43
|
5,77
|
7,21
|
8,72
|
10,3
|
12,0
|
13,7
|
|
0,05
|
1,43
|
2,11
|
3,01
|
4,07
|
5,22
|
6,45
|
7,74
|
9,10
|
10,5
|
12,0
|
|
0,1
|
1,40
|
1,99
|
2,75
|
3,62
|
4,55
|
5,54
|
6,56
|
7,63
|
8,73
|
9,87
|
|
0,3
|
1,34
|
1,81
|
2,37
|
2,99
|
3,64
|
4,31
|
4,99
|
5,70
|
6,42
|
7,15
|
|
0,5
|
1,31
|
1,73
|
2,21
|
2,73
|
3,26
|
3,81
|
4,37
|
4,94
|
5,52
|
6,11
|
|
1
|
1,27
|
1,62
|
2,00
|
2,40
|
2,81
|
3,21
|
3,63
|
4,04
|
4,46
|
4,87
|
|
3
|
1,21
|
1,45
|
1,69
|
1,93
|
2,17
|
2,40
|
2,63
|
2,86
|
3,08
|
3,29
|
|
5
|
1,18
|
1,37
|
1,56
|
1,74
|
1,91
|
2,08
|
2,24
|
2,39
|
2,54
|
2,68
|
|
10
|
1,13
|
1,26
|
1,38
|
1,48
|
1,58
|
1,68
|
1,76
|
1,84
|
1,91
|
1,98
|
|
20
|
1,08
|
1,15
|
1,20
|
1,24
|
1,28
|
1,31
|
1,33
|
1,36
|
1,37
|
1,38
|
|
25
|
1,06
|
1,11
|
1,14
|
1,16
|
1,18
|
1,20
|
1,21
|
1,21
|
1,21
|
1,21
|
|
30
|
1,04
|
1,07
|
1,09
|
1,10
|
1,10
|
1,11
|
1,10
|
1,10
|
1,09
|
1,07
|
|
40
|
1,02
|
1,02
|
1,01
|
0,997
|
0,981
|
0,963
|
0,942
|
0,92
|
0,896
|
0,87
|
|
50
|
0,991
|
0,97
|
0,942
|
0,912
|
0,881
|
0,850
|
0,817
|
0,784
|
0,751
|
0,717
|
|
60
|
0,967
|
0,925
|
0,882
|
0,838
|
0,795
|
0,753
|
0,711
|
0,671
|
0,632
|
0,594
|
|
70
|
0,943
|
0,882
|
0,823
|
0,768
|
0,715
|
0,664
|
0,616
|
0,57
|
0,527
|
0,486
|
|
75
|
0,929
|
0,859
|
0,794
|
0,732
|
0,675
|
0,621
|
0,57
|
0,522
|
0,478
|
0,436
|
|
80
|
0,915
|
0,835
|
0,762
|
0,696
|
0,634
|
0,577
|
0,523
|
0,474
|
0,429
|
0,387
|
|
90
|
0,880
|
0,777
|
0,689
|
0,612
|
0,542
|
0,479
|
0,422
|
0,37
|
0,325
|
0,284
|
|
95
|
0,852
|
0,734
|
0,637
|
0,553
|
0,479
|
0,413
|
0,355
|
0,304
|
0,260
|
0,222
|
|
97
|
0,835
|
0,708
|
0,606
|
0,520
|
0,444
|
0,377
|
0,319
|
0,269
|
0,226
|
0,190
|
|
99
|
0,804
|
0,664
|
0,555
|
0,464
|
0,386
|
0,319
|
0,262
|
0,214
|
0,175
|
0,142
|
|
99,5
|
0,788
|
0,641
|
0,529
|
0,437
|
0,358
|
0,291
|
0,236
|
0,189
|
0,152
|
0,121
|
|
99,7
|
0,777
|
0,626
|
0,513
|
0,419
|
0,34
|
0,274
|
0,219
|
0,174
|
0,138
|
0,108
|
|
99,9
|
0,757
|
0,599
|
0,482
|
0,388
|
0,309
|
0,244
|
0,191
|
0,148
|
0,114
|
0,088
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
|
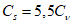
|
||||||||||
|
0,01
|
20,8
|
23,4
|
26,1
|
29,0
|
31,9
|
34,9
|
38,0
|
41,2
|
44,4
|
47,6
|
|
0,03
|
15,5
|
17,4
|
19,3
|
21,2
|
23,2
|
25,2
|
27,3
|
29,4
|
31,6
|
33,8
|
|
0,05
|
13,5
|
15,0
|
16,6
|
18,2
|
19,9
|
21,6
|
23,3
|
25,0
|
26,8
|
28,6
|
|
0,1
|
11,0
|
12,2
|
13,4
|
14,7
|
16,0
|
17,3
|
18,6
|
19,9
|
21,2
|
22,5
|
|
0,3
|
7,90
|
8,66
|
9,42
|
10,2
|
11,0
|
11,7
|
12,5
|
13,3
|
14,0
|
14,8
|
|
0,5
|
6,70
|
7,29
|
7,89
|
8,48
|
9,07
|
9,65
|
10,2
|
10,8
|
11,4
|
12,0
|
|
1
|
5,28
|
5,70
|
6,10
|
6,51
|
6,91
|
7,81
|
7,68
|
8,07
|
8,44
|
8,81
|
|
3
|
3,49
|
3,69
|
3,88
|
4,07
|
4,25
|
4,44
|
4,58
|
4,74
|
4,89
|
5,04
|
|
5
|
2,82
|
2,95
|
3,07
|
3,18
|
3,29
|
3,40
|
3,48
|
3,57
|
3,65
|
3,73
|
|
10
|
2,04
|
2,09
|
2,14
|
2,18
|
2,22
|
2,26
|
2,28
|
2,30
|
2,32
|
2,33
|
|
20
|
1,39
|
1,39
|
1,39
|
1,39
|
1,38
|
1,37
|
1,36
|
1,34
|
1,33
|
1,31
|
|
25
|
1,20
|
1,19
|
1,18
|
1,17
|
1,15
|
1,13
|
1,11
|
1,09
|
1,07
|
1,05
|
|
30
|
1,06
|
1,04
|
1,02
|
1,00
|
0,98
|
0,957
|
0,933
|
0,909
|
0,884
|
0,859
|
|
40
|
0,844
|
0,816
|
0,789
|
0,761
|
0,732
|
0,703
|
0,677
|
0,649
|
0,622
|
0,596
|
|
50
|
0,684
|
0,652
|
0,620
|
0,589
|
0,558
|
0,526
|
0,501
|
0,473
|
0,447
|
0,422
|
|
60
|
0,557
|
0,522
|
0,488
|
0,456
|
0,426
|
0,394
|
0,370
|
0,344
|
0,320
|
0,297
|
|
70
|
0,448
|
0,412
|
0,379
|
0,348
|
0,319
|
0,289
|
0,267
|
0,244
|
0,223
|
0,204
|
|
75
|
0,398
|
0,362
|
0,330
|
0,300
|
0,272
|
0,243
|
0,223
|
0,202
|
0,183
|
0,165
|
|
80
|
0,349
|
0,314
|
0,283
|
0,254
|
0,228
|
0,200
|
0,183
|
0,163
|
0,146
|
0,130
|
|
90
|
0,249
|
0,217
|
0,189
|
0,164
|
0,143
|
0,121
|
0,107
|
0,093
|
0,080
|
0,069
|
|
95
|
0,189
|
0,161
|
0,136
|
0,115
|
0,097
|
0,079
|
0,069
|
0,058
|
0,049
|
0,041
|
|
97
|
0,159
|
0,132
|
0,110
|
0,092
|
0,076
|
0,060
|
0,052
|
0,043
|
0,035
|
0,029
|
|
99
|
0,115
|
0,092
|
0,074
|
0,060
|
0,047
|
0,036
|
0,030
|
0,024
|
0,019
|
0,015
|
|
99,5
|
0,096
|
0,076
|
0,060
|
0,047
|
0,036
|
0,027
|
0,022
|
0,017
|
0,013
|
0,010
|
|
99,7
|
0,085
|
0,066
|
0,051
|
0,040
|
0,030
|
0,022
|
0,018
|
0,014
|
0,010
|
0,008
|
|
99,9
|
0,067
|
0,051
|
0,038
|
0,029
|
0,021
|
0,015
|
0,012
|
0,009
|
0,006
|
0,004
|
|
P
, %
|
|
|||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1,0
|
|
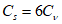
|
||||||||||
|
0,001
|
1,80
|
3,02
|
5,20
|
8,10
|
11,5
|
15,3
|
19,3
|
23,8
|
28,0
|
-
|
|
0,01
|
1,60
|
2,48
|
3,75
|
5,48
|
7,30
|
9,39
|
11,5
|
13,8
|
16,4
|
18,8
|
|
0,03
|
1,52
|
2,25
|
3,25
|
4,54
|
5,9
|
7,37
|
8,90
|
10,5
|
12,3
|
14,0
|
|
0,05
|
1,47
|
2,15
|
3,05
|
4,15
|
5,25
|
6,57
|
7,85
|
9,26
|
10,7
|
12,2
|
|
0,1
|
1,41
|
2,02
|
2,80
|
3,68
|
4,58
|
5,54
|
6,57
|
7,63
|
8,79
|
9,97
|
|
0,3
|
1,35
|
1,83
|
2,38
|
2,98
|
3,64
|
4,31
|
5,00
|
5,66
|
6,38
|
7,18
|
|
0,5
|
1,32
|
1,74
|
2,22
|
2,73
|
3,26
|
3,82
|
4,38
|
4,93
|
5,51
|
6,11
|
|
1
|
1,29
|
1,63
|
2,01
|
2,40
|
2,81
|
3,22
|
3,63
|
4,03
|
4,44
|
4,85
|
|
3
|
1,21
|
1,45
|
1,68
|
1,92
|
2,14
|
2,38
|
2,60
|
2,82
|
3,04
|
3,26
|
|
5
|
1,18
|
1,37
|
1,55
|
1,73
|
1,89
|
2,05
|
2,20
|
2,36
|
2,51
|
2,66
|
|
10
|
1,14
|
1,26
|
1,37
|
1,47
|
1,56
|
1,66
|
1,73
|
1,82
|
1,90
|
1,96
|
|
20
|
1,08
|
1,14
|
1,19
|
1,23
|
1,27
|
1,30
|
1,32
|
1,34
|
1,36
|
1,37
|
|
25
|
1,07
|
1,10
|
1,13
|
1,16
|
1,18
|
1,19
|
1,20
|
1,21
|
1,20
|
1,20
|
|
30
|
1,04
|
1,07
|
1,08
|
1,10
|
1,10
|
1,10
|
1,10
|
1,09
|
1,08
|
1,07
|
|
40
|
1,02
|
1,02
|
1,01
|
0,99
|
0,98
|
0,96
|
0,94
|
0,92
|
0,89
|
0,87
|
|
50
|
0,99
|
0,97
|
0,94
|
0,91
|
0,88
|
0,85
|
0,82
|
0,79
|
0,75
|
0,72
|
|
60
|
0,96
|
0,92
|
0,88
|
0,84
|
0,80
|
0,76
|
0,72
|
0,68
|
0,64
|
0,598
|
|
70
|
0,94
|
0,88
|
0,83
|
0,77
|
0,72
|
0,67
|
0,63
|
0,58
|
0,54
|
0,493
|
|
75
|
0,93
|
0,86
|
0,80
|
0,74
|
0,68
|
0,63
|
0,58
|
0,53
|
0,49
|
0,443
|
|
80
|
0,91
|
0,84
|
0,77
|
0,70
|
0,64
|
0,58
|
0,53
|
0,48
|
0,44
|
0,395
|
|
90
|
0,88
|
0,78
|
0,7
|
0,62
|
0,55
|
0,49
|
0,43
|
0,38
|
0,33
|
0,293
|
|
95
|
0,85
|
0,74
|
0,65
|
0,56
|
0,49
|
0,43
|
0,37
|
0,32
|
0,27
|
0,231
|
|
97
|
0,83
|
0,72
|
0,62
|
0,53
|
0,46
|
0,39
|
0,33
|
0,28
|
0,24
|
0,199
|
|
99
|
0,8
|
0,67
|
0,57
|
0,48
|
0,4
|
0,33
|
0,28
|
0,23
|
0,19
|
0,151
|
|
99,5
|
0,78
|
0,65
|
0,55
|
0,45
|
0,37
|
0,31
|
0,25
|
0,2
|
0,17
|
0,129
|
|
99,7
|
0,76
|
0,64
|
0,53
|
0,43
|
0,36
|
0,29
|
0,24
|
0,19
|
0,15
|
0,117
|
|
99,9
|
0,75
|
0,61
|
0,5
|
0,4
|
0,33
|
0,26
|
0,21
|
0,16
|
0,12
|
0,096
|
|
P
, %
|
|
|||||||||
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
|

|
||||||||||
|
0,01
|
21,4
|
24
|
26,8
|
29,6
|
32,6
|
35,7
|
39,1
|
41,9
|
45,1
|
48,4
|
|
0,03
|
15,8
|
17,7
|
19,6
|
21,6
|
23,6
|
25,6
|
27,8
|
29,8
|
32,0
|
34,2
|
|
0,05
|
13,7
|
15,2
|
16,8
|
18,4
|
20,1
|
21,8
|
23,6
|
25,2
|
27,0
|
28,8
|
|
0,1
|
11,1
|
12,3
|
13,6
|
14,8
|
16,0
|
17,3
|
18,6
|
19,9
|
21,2
|
22,5
|
|
0,3
|
7,92
|
8,67
|
9,42
|
10,2
|
10,9
|
11,7
|
12,5
|
13,0
|
14,0
|
14,7
|
|
0,5
|
6,69
|
7,28
|
7,86
|
8,45
|
9,04
|
9,61
|
10,2
|
10,7
|
11,3
|
11,9
|
|
1
|
5,26
|
5,67
|
6,07
|
6,46
|
6,85
|
7,24
|
7,59
|
7,96
|
8,35
|
8,71
|
|
3
|
3,46
|
3,66
|
3,85
|
4,03
|
4,20
|
4,37
|
4,51
|
4,68
|
4,83
|
4,97
|
|
5
|
2,79
|
2,92
|
3,04
|
3,15
|
3,25
|
3,35
|
3,43
|
3,53
|
3,60
|
3,68
|
|
10
|
2,02
|
2,07
|
2,12
|
2,16
|
2,20
|
2,23
|
2,25
|
2,28
|
2,29
|
2,31
|
|
20
|
1,38
|
1,38
|
1,38
|
1,38
|
1,37
|
1,36
|
1,35
|
1,34
|
1,32
|
1,31
|
|
25
|
1,20
|
1,19
|
1,18
|
1,16
|
1,15
|
1,13
|
1,11
|
1,09
|
1,07
|
1,05
|
|
30
|
1,06
|
1,04
|
1,02
|
1,00
|
0,973
|
0,957
|
0,935
|
0,91
|
0,887
|
0,863
|
|
40
|
0,844
|
0,818
|
0,791
|
0,764
|
0,736
|
0,703
|
0,684
|
0,655
|
0,630
|
0,604
|
|
50
|
0,688
|
0,656
|
0,625
|
0,594
|
0,565
|
0,536
|
0,511
|
0,481
|
0,456
|
0,432
|
|
60
|
0,562
|
0,528
|
0,495
|
0,464
|
0,434
|
0,406
|
0,382
|
0,353
|
0,330
|
0,308
|
|
70
|
0,455
|
0,42
|
0,387
|
0,357
|
0,328
|
0,302
|
0,280
|
0,353
|
0,233
|
0,214
|
|
75
|
0,406
|
0,371
|
0,338
|
0,309
|
0,281
|
0,256
|
0,236
|
0,211
|
0,192
|
0,175
|
|
80
|
0,357
|
0,323
|
0,291
|
0,263
|
0,237
|
0,213
|
0,195
|
0,172
|
0,155
|
0,139
|
|
90
|
0,257
|
0,226
|
0,198
|
0,173
|
0,152
|
0,132
|
0,188
|
0,100
|
0,088
|
0,076
|
|
95
|
0,198
|
0,169
|
0,145
|
0,123
|
0,105
|
0,089
|
0,078
|
0,064
|
0,055
|
0,046
|
|
97
|
0,167
|
0,141
|
0,118
|
0,099
|
0,083
|
0,069
|
0,06
|
0,048
|
0,040
|
0,033
|
|
99
|
0,123
|
0,100
|
0,081
|
0,066
|
0,053
|
0,043
|
0,036
|
0,027
|
0,022
|
0,018
|
|
99,5
|
0,104
|
0,083
|
0,066
|
0,053
|
0,042
|
0,033
|
0,027
|
0,02
|
0,016
|
0,012
|
|
99,7
|
0,092
|
0,073
|
0,057
|
0,045
|
0,035
|
0,027
|
0,022
|
0,016
|
0,013
|
0,010
|
|
99,9
|
0,074
|
0,057
|
0,044
|
0,033
|
0,025
|
0,019
|
0,015
|
0,011
|
0,008
|
0,006
|
Таблица Б.2
Нормированные отклонения от среднего значения ординат
распределения Пирсона III типа
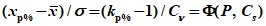
(биномиальная кривая распределения)
|
C
s
|
P
, %
|
|||||||||||
|
0,01
|
0,1
|
1,0
|
3,0
|
5,0
|
10
|
20
|
25
|
30
|
40
|
50
|
60
|
|
|
-4,0
|
0,500
|
0,500
|
0,500
|
0,500
|
0,500
|
0,500
|
0,500
|
0,49
|
0,49
|
0,46
|
0,41
|
0,31
|
|
-3,8
|
0,527
|
0,527
|
0,526
|
0,526
|
0,526
|
0,526
|
0,520
|
0,52
|
0,51
|
0,48
|
0,42
|
0,30
|
|
-3,6
|
0,556
|
0,556
|
0,556
|
0,556
|
0,556
|
0,555
|
0,550
|
0,54
|
0,54
|
0,49
|
0,42
|
0,28
|
|
-3,4
|
0,588
|
0,588
|
0,588
|
0,588
|
0,587
|
0,586
|
0,580
|
0,57
|
0,55
|
0,50
|
0,41
|
0,27
|
|
-3,2
|
0,625
|
0,625
|
0,625
|
0,625
|
0,625
|
0,621
|
0,610
|
0,59
|
0,57
|
0,51
|
0,41
|
0,25
|
|
-3,0
|
0,667
|
0,667
|
0,666
|
0,666
|
0,665
|
0,661
|
0,640
|
0,62
|
0,59
|
0,51
|
0,40
|
0,22
|
|
-2,8
|
0,715
|
0,715
|
0,715
|
0,714
|
0,711
|
0,703
|
0,670
|
0,64
|
0,60
|
0,51
|
0,39
|
0,20
|
|
-2,6
|
0,770
|
0,770
|
0,770
|
0,766
|
0,764
|
0,746
|
0,700
|
0,66
|
0,61
|
0,51
|
0,37
|
0,17
|
|
-2,4
|
0,835
|
0,833
|
0,830
|
0,826
|
0,820
|
0,792
|
0,720
|
0,67
|
0,62
|
0,51
|
0,35
|
0,17
|
|
-2,2
|
0,914
|
0,910
|
0,905
|
0,895
|
0,882
|
0,842
|
0,750
|
0,69
|
0,64
|
0,50
|
0,33
|
0,12
|
|
-2,0
|
1,01
|
1,00
|
0,990
|
0,970
|
0,950
|
0,900
|
0,780
|
0,71
|
0,64
|
0,49
|
0,31
|
0,09
|
|
-1,8
|
1,11
|
1,11
|
1,09
|
1,06
|
1,02
|
0,940
|
0,800
|
0,72
|
0,64
|
0,48
|
0,28
|
0,05
|
|
-1,6
|
1,26
|
1,24
|
1,20
|
1,14
|
1,10
|
0,990
|
0,810
|
0,73
|
0,64
|
0,46
|
0,25
|
0,02
|
|
-1,4
|
1,41
|
1,39
|
1,32
|
1,23
|
1,17
|
1,04
|
0,830
|
0,73
|
0,64
|
0,44
|
0,22
|
-0,20
|
|
-1,2
|
1,68
|
1,58
|
1,45
|
1,33
|
1,24
|
1,08
|
0,840
|
0,74
|
0,63
|
0,42
|
0,19
|
-0,05
|
|
-1,0
|
1,92
|
1,79
|
1,59
|
1,42
|
1,32
|
1,13
|
0,850
|
0,73
|
0,62
|
0,39
|
0,16
|
-0,09
|
|
-0,8
|
2,23
|
2,02
|
1,74
|
1,52
|
1,38
|
1,17
|
0,860
|
0,73
|
0,60
|
0,37
|
0,13
|
-0,12
|
|
-0,6
|
2,57
|
2,27
|
1,88
|
1,61
|
1,45
|
1,20
|
0,850
|
0,72
|
0,59
|
0,34
|
0,10
|
-0,16
|
|
-0,4
|
2,98
|
2,54
|
2,03
|
1,70
|
1,52
|
1,23
|
0,850
|
0,71
|
0,57
|
0,31
|
0,07
|
-0,19
|
|
-0,2
|
3,37
|
2,81
|
2,18
|
1,79
|
1,58
|
1,26
|
0,850
|
0,69
|
0,55
|
0,28
|
0,03
|
-0,22
|
|
0,0
|
3,72
|
3,09
|
2,33
|
1,88
|
1,64
|
1,28
|
0,840
|
0,67
|
0,52
|
0,25
|
0,00
|
-0,25
|
|
0,2
|
4,16
|
3,38
|
2,47
|
1,96
|
1,70
|
1,30
|
0,83
|
0,65
|
0,50
|
0,22
|
-0,03
|
-0,28
|
|
0,4
|
4,61
|
3,66
|
2,61
|
2,04
|
1,75
|
1,32
|
0,82
|
0,63
|
0,47
|
0,19
|
-0,07
|
-0,31
|
|
0,6
|
5,05
|
3,96
|
2,75
|
2,12
|
1,80
|
1,33
|
0,80
|
0,61
|
0,44
|
0,16
|
-0,10
|
-0,34
|
|
0,8
|
5,50
|
4,24
|
2,89
|
2,18
|
1,84
|
1,34
|
0,78
|
0,58
|
0,41
|
0,12
|
-0,13
|
-0,37
|
|
1,0
|
5,96
|
4,53
|
3,02
|
2,25
|
1,88
|
1,34
|
0,76
|
0,55
|
0,38
|
0,09
|
-0,16
|
-0,39
|
|
1,2
|
6,41
|
4,81
|
3,15
|
2,31
|
1,92
|
1,34
|
0,73
|
0,52
|
0,35
|
0,05
|
-0,19
|
-0,42
|
|
1,4
|
6,87
|
5,09
|
3,27
|
2,37
|
1,95
|
1,34
|
0,71
|
0,49
|
0,31
|
0,02
|
-0,22
|
-0,44
|
|
1,6
|
7,31
|
5,37
|
3,39
|
2,42
|
1,97
|
1,33
|
0,68
|
0,46
|
0,28
|
-0,02
|
-0,25
|
-0,46
|
|
1,8
|
7,76
|
5,64
|
3,50
|
2,46
|
1,99
|
1,32
|
0,64
|
0,42
|
0,24
|
-0,05
|
-0,28
|
-0,48
|
|
2,0
|
8,21
|
5,91
|
3,60
|
2,51
|
2,00
|
1,30
|
0,61
|
0,39
|
0,20
|
-0,08
|
-0,31
|
-0,49
|
|
2,2
|
8,63
|
6,14
|
3,68
|
2,54
|
2,02
|
1,27
|
0,57
|
0,35
|
0,16
|
-0,12
|
-0,33
|
-0,50
|
|
2,4
|
9,00
|
6,37
|
3,78
|
2,60
|
2,00
|
1,25
|
0,52
|
0,29
|
0,12
|
-0,14
|
-0,35
|
-0,51
|
|
2,6
|
9,39
|
6,54
|
3,86
|
2,63
|
2,00
|
1,21
|
0,48
|
0,25
|
0,085
|
-0,17
|
-0,37
|
-0,51
|
|
2,8
|
9,77
|
6,86
|
3,96
|
2,65
|
2,00
|
1,18
|
0,44
|
0,22
|
0,057
|
-0,20
|
-0,39
|
-0,51
|
|
3,0
|
10,16
|
7,10
|
4,05
|
2,66
|
1,97
|
1,13
|
0,39
|
0,19
|
0,027
|
-0,22
|
-0,40
|
-0,51
|
|
3,2
|
10,55
|
7,35
|
4,11
|
2,66
|
1,96
|
1,09
|
0,35
|
0,15
|
-0,006
|
-0,25
|
-0,41
|
-0,51
|
|
3,4
|
10,9
|
7,54
|
4,18
|
2,66
|
1,94
|
1,06
|
0,31
|
0,11
|
-0,036
|
-0,27
|
-0,41
|
-0,50
|
|
3,6
|
11,3
|
7,72
|
4,24
|
2,66
|
1,93
|
1,03
|
0,28
|
0,064
|
-0,072
|
-0,28
|
-0,42
|
-0,49
|
|
3,8
|
11,67
|
7,97
|
4,29
|
2,65
|
1,90
|
1,00
|
0,24
|
0,032
|
-0,095
|
-0,30
|
-0,42
|
-0,48
|
|
4,0
|
12,02
|
8,17
|
4,34
|
2,65
|
1,90
|
0,96
|
0,21
|
0,010
|
-0,120
|
-0,31
|
-0,41
|
-0,46
|
|
4,2
|
12,40
|
8,38
|
4,39
|
2,64
|
1,88
|
0,93
|
0,19
|
-0,010
|
-0,13
|
-0,31
|
-0,41
|
-0,45
|
|
4,4
|
12,76
|
8,60
|
4,42
|
2,63
|
1,86
|
0,91
|
0,15
|
-0,032
|
-0,15
|
-0,32
|
-0,40
|
-0,44
|
|
4,6
|
13,12
|
8,79
|
4,46
|
2,62
|
1,84
|
0,87
|
0,13
|
-0,052
|
-0,17
|
-0,32
|
-0,40
|
-0,42
|
|
4,8
|
13,51
|
8,96
|
4,50
|
2,60
|
1,81
|
0,82
|
0,10
|
-0,075
|
-0,19
|
-0,32
|
-0,39
|
-0,41
|
|
5,0
|
13,87
|
9,12
|
4,54
|
2,60
|
1,78
|
0,78
|
0,068
|
-0,099
|
-0,20
|
-0,33
|
-0,38
|
-0,40
|
|
5,2
|
14,25
|
9,27
|
4,59
|
2,60
|
1,74
|
0,73
|
0,035
|
-0,120
|
-0,21
|
-0,30
|
-0,37
|
-0,38
|
|
5,4
|
14,60
|
9,42
|
4,62
|
2,60
|
1,70
|
0,67
|
0,02
|
-0,100
|
-0,21
|
-0,30
|
-0,37
|
-0,37
|
|
5,6
|
14,95
|
9,59
|
4,65
|
2,60
|
1,67
|
0,62
|
0,0
|
-0,120
|
-0,21
|
-0,30
|
-0,36
|
-0,36
|
|
5,8
|
15,32
|
9,70
|
4,70
|
2,60
|
1,64
|
0,57
|
-0,02
|
-0,140
|
-0,21
|
-0,30
|
-0,35
|
-0,35
|
|
6,0
|
15,67
|
9,84
|
4,70
|
2,60
|
1,60
|
0,51
|
-0,05
|
-0,150
|
-0,21
|
-0,30
|
-0,34
|
-0,34
|
|
6,2
|
16,04
|
9,95
|
4,71
|
2,60
|
1,56
|
0,47
|
-0,05
|
-0,150
|
-0,21
|
-0,30
|
-0,34
|
-0,34
|
|
6,4
|
16,40
|
10,05
|
4,71
|
2,60
|
1,52
|
0,42
|
-0,05
|
-0,150
|
-0,21
|
-0,30
|
-0,33
|
-0,39
|
|
C
s
|
P
, %
|
|||||||
|
70
|
75
|
80
|
90
|
95
|
97
|
99
|
99,9
|
|
|
-4,0
|
-0,120
|
-0,010
|
-0,21
|
-0,96
|
-1,90
|
-2,65
|
-4,34
|
-8,17
|
|
-3,8
|
-0,095
|
-0,032
|
-0,24
|
-1,00
|
-1,90
|
-2,65
|
-4,29
|
-7,97
|
|
-3,6
|
-0,072
|
-0,064
|
-0,28
|
-1,03
|
-1,93
|
-2,66
|
-4,24
|
-7,72
|
|
-3,4
|
-0,036
|
-0,11
|
-0,31
|
-1,06
|
-1,94
|
-2,66
|
-4,18
|
-7,54
|
|
-3,2
|
-0,006
|
-0,15
|
-0,35
|
-1,09
|
-1,96
|
-2,66
|
-4,11
|
-7,35
|
|
-3,0
|
-0,027
|
-0,19
|
-0,39
|
-1,13
|
-1,97
|
-2,66
|
-4,05
|
-7,10
|
|
-2,8
|
-0,057
|
-0,22
|
-0,44
|
-1,18
|
-2,00
|
-2,65
|
-3,86
|
-6,86
|
|
-2,6
|
-0,085
|
-0,25
|
-0,48
|
-1,21
|
-2,00
|
-2,63
|
-3,86
|
-6,54
|
|
-2,4
|
-0,12
|
-0,29
|
-0,52
|
-1,25
|
-2,00
|
-2,60
|
-3,78
|
-6,37
|
|
-2,2
|
-0,16
|
-0,35
|
-0,57
|
-1,27
|
-2,02
|
-2,54
|
-3,68
|
-6,14
|
|
-2,0
|
-0,20
|
-0,39
|
-0,61
|
-1,30
|
-2,00
|
-2,51
|
-3,60
|
-5,91
|
|
-1,8
|
-0,24
|
-0,42
|
-0,64
|
-1,32
|
-1,99
|
-2,46
|
-3,50
|
-5,64
|
|
-1,6
|
-0,28
|
-0,46
|
-0,68
|
-1,33
|
-1,97
|
-2,42
|
-3,39
|
-5,37
|
|
-1,4
|
-0,31
|
-0,49
|
-0,71
|
-1,34
|
-1,95
|
-2,37
|
-3,27
|
-5,09
|
|
-1,2
|
-0,35
|
-0,52
|
-0,73
|
-1,34
|
1,92
|
-2,31
|
-3,15
|
-4,81
|
|
-1,0
|
-0,38
|
-0,55
|
-0,76
|
-1,34
|
-1,88
|
-2,25
|
-3,02
|
-4,53
|
|
-0,8
|
-0,41
|
-0,58
|
-0,79
|
-1,34
|
-1,84
|
-2,18
|
-2,89
|
-4,24
|
|
-0,6
|
-0,44
|
-0,61
|
-0,80
|
-1,33
|
-1,80
|
-2,12
|
-2,75
|
-3,96
|
|
-0,4
|
-0,47
|
-0,63
|
-0,82
|
-1,32
|
-1,75
|
-2,04
|
-2,61
|
-3,66
|
|
-0,2
|
-0,50
|
-0,65
|
-0,83
|
-1,30
|
-1,70
|
-1,96
|
-2,47
|
-3,38
|
|
0,0
|
-0,52
|
-0,67
|
-0,84
|
-1,28
|
-1,64
|
-1,88
|
-2,33
|
-3,09
|
|
0,2
|
-0,55
|
-0,69
|
-0,85
|
-1,26
|
-1,58
|
-1,79
|
-2,18
|
-2,81
|
|
0,4
|
-0,57
|
-0,71
|
-0,85
|
-1,23
|
-1,52
|
-1,70
|
-2,03
|
-2,54
|
|
0,6
|
-0,59
|
-0,72
|
-0,85
|
-1,20
|
-1,45
|
-1,61
|
-1,88
|
-2,27
|
|
0,8
|
-0,60
|
-0,73
|
-0,86
|
-1,17
|
-1,38
|
-1,52
|
-1,74
|
-2,02
|
|
1,0
|
-0,62
|
-0,73
|
-0,85
|
-1,13
|
-1,32
|
-1,42
|
-1,59
|
-1,79
|
|
1,2
|
-0,63
|
-0,74
|
-0,84
|
-1,08
|
-1,24
|
-1,33
|
-1,45
|
-1,58
|
|
1,4
|
-0,64
|
-0,73
|
-0,83
|
-1,04
|
-1,17
|
-1,23
|
-1,32
|
-1,39
|
|
1,6
|
-0,64
|
-0,73
|
-0,81
|
-0,99
|
-1,10
|
-1,14
|
-1,20
|
-1,24
|
|
1,8
|
-0,64
|
-0,72
|
-0,80
|
-0,94
|
-1,02
|
-1,06
|
-1,09
|
-1,11
|
|
2,0
|
-0,64
|
-0,71
|
-0,78
|
-0,90
|
-0,95
|
-0,97
|
-0,99
|
-1,00
|
|
2,2
|
-0,64
|
-0,69
|
-0,75
|
-0,842
|
-0,882
|
-0,895
|
-0,905
|
-0,910
|
|
2,4
|
-0,62
|
-0,67
|
-0,72
|
-0,792
|
-0,820
|
-0,826
|
-0,830
|
-0,833
|
|
2,6
|
-0,61
|
-0,66
|
-0,70
|
-0,746
|
-0,764
|
-0,766
|
-0,770
|
-0,770
|
|
2,8
|
-0,60
|
-0,64
|
-0,67
|
-0,703
|
-0,711
|
-0,714
|
-0,715
|
-0,715
|
|
3,0
|
-0,59
|
-0,62
|
-0,64
|
-0,661
|
-0,665
|
-0,666
|
-0,666
|
-0,667
|
|
3,2
|
-0,57
|
-0,59
|
-0,61
|
-0,621
|
-0,625
|
-0,625
|
-0,625
|
-0,625
|
|
3,4
|
-0,55
|
-0,57
|
-0,58
|
-0,586
|
-0,587
|
-0,588
|
-0,588
|
-0,588
|
|
3,6
|
-0,54
|
-0,54
|
-0,55
|
-0,555
|
-0,556
|
-0,556
|
-0,556
|
-0,556
|
|
3,8
|
-0,51
|
-0,52
|
-0,52
|
-0,526
|
-0,526
|
-0,526
|
-0,526
|
-0,527
|
|
4,0
|
-0,49
|
-0,49
|
-0,50
|
-0,500
|
-0,500
|
-0,500
|
-0,500
|
-0,500
|
|
4,2
|
-0,47
|
-0,473
|
-0,475
|
-0,476
|
-0,476
|
-0,476
|
-0,477
|
-0,477
|
|
4,4
|
-0,451
|
-0,454
|
-0,455
|
-0,455
|
-0,455
|
-0,455
|
-0,455
|
-0,455
|
|
4,6
|
-0,432
|
-0,454
|
-0,435
|
-0,435
|
-0,435
|
-0,435
|
-0,435
|
-0,435
|
|
4,8
|
-0,416
|
-0,416
|
-0,416
|
-0,416
|
-0,416
|
-0,416
|
-0,417
|
-0,417
|
|
5,0
|
-0,399
|
-0,400
|
-0,400
|
-0,400
|
-0,400
|
-0,400
|
-0,400
|
-0,400
|
|
5,2
|
-0,384
|
-0,385
|
-0,385
|
-0,385
|
-0,385
|
-0,385
|
-0,385
|
-0,385
|
|
5,4
|
-0,37
|
-0,37
|
-0,37
|
-0,37
|
-0,37
|
-0,37
|
-0,37
|
-0,37
|
|
5,6
|
-0,36
|
-0,36
|
-0,36
|
-0,36
|
-0,36
|
-0,36
|
-0,36
|
-0,36
|
|
5,8
|
-0,35
|
-0,35
|
-0,35
|
-0,35
|
-0,35
|
-0,35
|
-0,35
|
-0,35
|
|
6,0
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
|
6,2
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
-0,34
|
|
6,4
|
-0,33
|
-0,33
|
-0,33
|
-0,33
|
-0,33
|
-0,33
|
-0,33
|
-0,33
|
Таблица Б.3
и
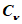 методом приближенно наибольшего правдоподобия
методом приближенно наибольшего правдоподобия
при трех свободно назначаемых параметрах
|
|

|

|
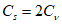
|
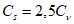
|
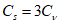
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,10
|
-0,00219
|
0,00218
|
-0,00218
|
0,00217
|
-0,00218
|
0,00217
|
(-0,00217)
|
(0,00216)
|
(-0,00216)
|
(0,00216)
|
|
0,15
|
-0,00498
|
0,00490
|
-0,00494
|
0,00489
|
-0,00490
|
0,00487
|
-0,00486
|
0,00484
|
(-0,00482)
|
(0,00482)
|
|
0,20
|
-0,00897
|
0,00876
|
-0,00886
|
0,00868
|
-0,00874
|
0,00863
|
-0,00863
|
0,00857
|
(-0,00853)
|
(0,00854)
|
|
0,25
|
-0,01433
|
0,01371
|
-0,01401
|
0,01357
|
-0,01371
|
0,01343
|
-0,01344
|
0,01330
|
(-0,01315)
|
(0,01316)
|
|
0,30
|
-0,02117
|
0,01987
|
-0,02046
|
0,01953
|
-0,01984
|
0,01925
|
-0,01928
|
0,01900
|
(-0,01875)
|
(0,01875)
|
|
0,35
|
-0,02971
|
0,02712
|
-0,02832
|
0,02656
|
-0,02714
|
0,02605
|
-0,02614
|
0,02560
|
-0,02528
|
0,02519
|
|
0,40
|
-0,04022
|
0,03561
|
-0,03772
|
0,03466
|
-0,03567
|
0,03382
|
-0,03400
|
0,03308
|
-0,03262
|
0,03242
|
|
0,45
|
-0,05305
|
0,04529
|
-0,04879
|
0,04380
|
-0,04545
|
0,04249
|
-0,04283
|
0,04137
|
-0,04076
|
0,04031
|
|
0,50
|
-0,06860
|
0,05677
|
-0,06173
|
0,05395
|
-0,05653
|
0,05204
|
-0,05265
|
0,05042
|
-0,04968
|
0,04906
|
|
0,55
|
-0,08719
|
0,06823
|
-0,07670
|
0,06508
|
-0,06897
|
0,06240
|
-0,06342
|
0,06018
|
-0,05935
|
0,05835
|
|
0,60
|
-0,10939
|
0,08145
|
-0,09300
|
0,07715
|
-0,08281
|
0,07354
|
-0,07516
|
0,07060
|
-0,06975
|
0,06821
|
|
0,65
|
-0,13563
|
0,09575
|
-0,11259
|
0,09014
|
-0,09810
|
0,08539
|
-0,08784
|
0,08161
|
-0,08085
|
0,07860
|
|
0,70
|
-0,16635
|
0,11108
|
-0,13584
|
0,10388
|
-0,11490
|
0,09790
|
-0,10148
|
0,09317
|
-0,09265
|
0,08947
|
|
0,75
|
-0,20200
|
0,12735
|
-0,16098
|
0,11841
|
-0,13328
|
0,11101
|
-0,11608
|
0,10563
|
-0,10513
|
0,10077
|
|
0,80
|
-0,24296
|
0,14446
|
-0,18918
|
0,13362
|
-0,15328
|
0,12467
|
-0,13164
|
0,11774
|
-0,11828
|
0,11246
|
|
0,85
|
-0,29000
|
0,16232
|
-0,22053
|
0,14944
|
-0,17496
|
0,13881
|
-0,14818
|
0,13065
|
-0,13210
|
0,12451
|
|
0,90
|
-0,34218
|
0,18081
|
-0,25530
|
0,16578
|
-0,19839
|
0,15339
|
-16569
|
0,14392
|
-0,14658
|
0,13686
|
|
0,95
|
-0,40097
|
0,19989
|
-0,29358
|
0,18259
|
-0,22361
|
0,16834
|
-0,18420
|
0,15751
|
-0,16171
|
0,14950
|
|
1,00
|
-0,46614
|
0,21933
|
-0,33552
|
0,19978
|
-0,25068
|
0,18361
|
-0,20371
|
0,17137
|
-0,17749
|
0,16237
|
|
1,05
|
-0,53779
|
0,23916
|
-0,38121
|
0,21728
|
-0,27964
|
0,19916
|
-0,22424
|
0,18547
|
-0,19393
|
0,17546
|
|
1,10
|
-0,61597
|
0,25924
|
-0,43080
|
0,23505
|
-0,31055
|
0,21394
|
-0,24581
|
0,19978
|
-0,21102
|
0,18872
|
|
1,15
|
-0,70065
|
0,27950
|
-0,48428
|
0,25301
|
-0,34344
|
0,23090
|
-0,26843
|
0,21426
|
-0,22877
|
0,20216
|
|
1,20
|
-0,79160
|
0,29984
|
-0,54175
|
0,27111
|
-0,37836
|
0,24601
|
-0,29212
|
0,22888
|
-0,24717
|
0,21571
|
|
1,25
|
-
|
-
|
-0,60331
|
0,28930
|
-0,41635
|
0,26323
|
-0,31691
|
0,24360
|
-0,26604
|
0,22938
|
|
1,30
|
-
|
-
|
-0,66895
|
0,30755
|
-0,45442
|
0,27953
|
-0,34280
|
0,25842
|
-0,28507
|
0,24313
|
|
1,35
|
-
|
-
|
-0,73874
|
0,32581
|
-0,49563
|
0,29587
|
-0,36994
|
0,27340
|
-0,30637
|
0,25695
|
|
1,40
|
-
|
-
|
-0,81267
|
0,34405
|
-0,53808
|
0,31222
|
-0,39839
|
0,28815
|
-0,32744
|
0,27081
|
|
1,45
|
-
|
-
|
-0,89078
|
0,36223
|
-0,58452
|
0,32858
|
-0,42730
|
0,30316
|
-0,34920
|
0,28470
|
|
1,50
|
-
|
-
|
-0,97307
|
0,38034
|
-0,63225
|
0,34490
|
-0,45781
|
0,31810
|
-0,37166
|
0,29861
|
|
1,55
|
-
|
-
|
-1,05955
|
0,39835
|
-0,68220
|
0,36117
|
-0,36117
|
0,33302
|
-0,39480
|
0,31252
|
|
1,60
|
-
|
-
|
-1,15022
|
0,41624
|
-0,73440
|
0,37738
|
-0,37738
|
0,34792
|
-0,41865
|
0,32641
|
|
1,65
|
-
|
-
|
-1,24510
|
0,43399
|
-0,78884
|
0,39351
|
-0,39351
|
0,36277
|
-0,44321
|
0,34029
|
|
1,70
|
-
|
-
|
-1,34415
|
0,45159
|
-0,87554
|
0,40054
|
-0,40054
|
0,37756
|
-0,46850
|
0,35412
|
|
1,75
|
-
|
-
|
-1,44768
|
0,46904
|
-0,90453
|
0,42548
|
-0,42548
|
0,39229
|
-0,49451
|
0,36791
|
|
1,80
|
-
|
-
|
-155479
|
0,48631
|
-0,96580
|
0,44130
|
-0,44130
|
0,40695
|
-0,52130
|
0,38165
|
|
1,85
|
-
|
-
|
-1,66636
|
0,50340
|
-1,02936
|
0,45609
|
-0,45609
|
0,42152
|
-0,54877
|
0,39532
|
|
1,90
|
-
|
-
|
-1,78209
|
0,52031
|
-1,09523
|
0,47256
|
-0,47256
|
0,43599
|
-0,57792
|
0,40893
|
|
1,95
|
-
|
-
|
-1,90196
|
0,53703
|
-1,16340
|
0,48799
|
-0,48799
|
0,46038
|
-0,60604
|
0,42247
|
|
2,00
|
-
|
-
|
-2,02597
|
0,55356
|
-1,23389
|
0,50327
|
-0,50327
|
0,46466
|
-0,63584
|
0,43592
|
Таблица Б.4
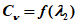 для вычисления
для вычисления
наибольшего правдоподобия при закрепленном
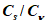
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
|
||||||||||
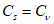
|
||||||||||
|
0,10
|
0,0022
|
0,0026
|
0,0032
|
0,0038
|
0,0044
|
0,0050
|
0,0058
|
0,0066
|
0,0074
|
0,0082
|
|
0,20
|
0,0090
|
0,0100
|
0,0111
|
0,0122
|
0,0132
|
0,0143
|
0,0157
|
0,0171
|
0,0184
|
0,0199
|
|
0,30
|
0,0212
|
0,0229
|
0,0246
|
0,0263
|
0,0280
|
0,0297
|
0,0318
|
0,0339
|
0,0360
|
0,0381
|
|
0,40
|
0,0402
|
0,0428
|
0,0454
|
0,0479
|
0,0505
|
0,0530
|
0,0562
|
0,0593
|
0,0624
|
0,0655
|
|
0,50
|
0,0686
|
0,0723
|
0,0760
|
0,0797
|
0,0835
|
0,0872
|
0,0916
|
0,0961
|
0,101
|
0,105
|
|
0,60
|
0,109
|
0,115
|
0,120
|
0,125
|
0,130
|
0,136
|
0,142
|
0,148
|
0,154
|
0,160
|
|
0,70
|
0,166
|
0,173
|
0,181
|
0,188
|
0,195
|
0,202
|
0,210
|
0,218
|
0,227
|
0,235
|
|
0,80
|
0,243
|
0,252
|
0,262
|
0,271
|
0,281
|
0,290
|
0,300
|
0,311
|
0,321
|
0,332
|
|
0,90
|
0,342
|
0,354
|
0,366
|
0,377
|
0,389
|
0,401
|
0,414
|
0,427
|
0,440
|
0,453
|
|
1,00
|
0,466
|
0,480
|
0,495
|
0,509
|
0,523
|
0,538
|
0,553
|
0,569
|
0,585
|
0,600
|
|
1,10
|
0,616
|
0,633
|
0,650
|
0,668
|
0,684
|
0,701
|
0,719
|
0,737
|
0,755
|
0,773
|
|
1,20
|
0,792
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
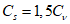
|
||||||||||
|
0,10
|
0,0022
|
0,0026
|
0,0031
|
0,0037
|
0,0043
|
0,0049
|
0,0057
|
0,0065
|
0,0073
|
0,0081
|
|
0,20
|
0,0089
|
0,0099
|
0,0109
|
0,0120
|
0,0130
|
0,0140
|
0,0153
|
0,0166
|
0,0178
|
0,0192
|
|
0,30
|
0,0205
|
0,0220
|
0,0236
|
0,0252
|
0,0267
|
0,0283
|
0,0302
|
0,0321
|
0,0340
|
0,0358
|
|
0,40
|
0,0377
|
0,0399
|
0,0421
|
0,0444
|
0,0466
|
0,0488
|
0,0514
|
0,0540
|
0,0566
|
0,0591
|
|
0,50
|
0,0617
|
0,0647
|
0,0677
|
0,0707
|
0,0737
|
0,0767
|
0,0800
|
0,0832
|
0,0865
|
0,0897
|
|
0,60
|
0,0930
|
0,0969
|
0,101
|
0,105
|
0,109
|
0,113
|
0,117
|
0,122
|
0,127
|
0,131
|
|
0,70
|
0,136
|
0,141
|
0,146
|
0,151
|
0,156
|
0,161
|
0,167
|
0,172
|
0,178
|
0,184
|
|
0,80
|
0,189
|
0,195
|
0,202
|
0,208
|
0,214
|
0,221
|
0,227
|
0,234
|
0,241
|
0,248
|
|
0,90
|
0,255
|
0,263
|
0,271
|
0,278
|
0,286
|
0,294
|
0,302
|
0,310
|
0,319
|
0,327
|
|
1,00
|
0,336
|
0,345
|
0,354
|
0,363
|
0,372
|
0,381
|
0,391
|
0,401
|
0,411
|
0,421
|
|
1,10
|
0,431
|
0,441
|
0,452
|
0,463
|
0,474
|
0,484
|
0,496
|
0,507
|
0,519
|
0,530
|
|
1,20
|
0,542
|
0,554
|
0,566
|
0,579
|
0,591
|
0,603
|
0,616
|
0,630
|
0,643
|
0,656
|
|
1,30
|
0,669
|
0,683
|
0,697
|
0,711
|
0,725
|
0,739
|
0,754
|
0,768
|
0,783
|
0,798
|
|
1,40
|
0,813
|
0,828
|
0,844
|
0,860
|
0,875
|
0,891
|
0,907
|
0,924
|
0,940
|
0,957
|
|
1,50
|
0,973
|
0,990
|
1,008
|
1,025
|
1,042
|
1,060
|
1,078
|
1,096
|
1,114
|
1,132
|
|
1,60
|
1,150
|
1,169
|
1,188
|
1,207
|
1,226
|
1,245
|
1,265
|
1,285
|
1,305
|
1,324
|
|
1,70
|
1,344
|
1,365
|
1,386
|
1,406
|
1,427
|
1,448
|
1,469
|
1,491
|
1,512
|
1,533
|
|
1,80
|
1,555
|
1,577
|
1,599
|
1,622
|
1,644
|
1,666
|
1,690
|
1,713
|
1,736
|
1,759
|
|
1,90
|
1,782
|
1,806
|
1,830
|
1,854
|
1,878
|
1,902
|
1,927
|
1,952
|
1,976
|
2,001
|
|
2,00
|
2,026
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
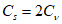
|
||||||||||
|
0,10
|
0,0022
|
0,0026
|
0,0031
|
0,0037
|
0,0043
|
0,0049
|
0,0056
|
0,0063
|
0,0071
|
0,0079
|
|
0,20
|
0,0087
|
0,0096
|
0,0106
|
0,0116
|
0,0126
|
0,0137
|
0,0148
|
0,0160
|
0,0172
|
0,0185
|
|
0,30
|
0,0198
|
0,0212
|
0,0226
|
0,0241
|
0,0256
|
0,0271
|
0,0287
|
0,0304
|
0,0321
|
0,0339
|
|
0,40
|
0,0357
|
0,0357
|
0,0394
|
0,0414
|
0,0434
|
0,0454
|
0,0476
|
0,0497
|
0,0519
|
0,0542
|
|
0,50
|
0,0565
|
0,0589
|
0,0613
|
0,0638
|
0,0664
|
0,069
|
0,0716
|
0,0743
|
0,0771
|
0,0799
|
|
0,60
|
0,0828
|
0,0858
|
0,0887
|
0,0918
|
0,0949
|
0,0981
|
0,101
|
0,105
|
0,108
|
0,11
|
|
0,70
|
0,115
|
0,118
|
0,122
|
0,126
|
0,129
|
0,133
|
0,137
|
0,141
|
0,145
|
0,149
|
|
0,80
|
0,153
|
0,157
|
0,162
|
0,166
|
0,170
|
0,175
|
0,180
|
0,184
|
0,189
|
0,194
|
|
0,90
|
0,198
|
0,203
|
0,208
|
0,213
|
0,218
|
0,224
|
0,229
|
0,234
|
0,240
|
0,245
|
|
1,00
|
0,251
|
0,256
|
0,262
|
0,268
|
0,274
|
0,280
|
0,286
|
0,292
|
0,298
|
0,304
|
|
1,10
|
0,311
|
0,317
|
0,323
|
0,330
|
0,337
|
0,343
|
0,350
|
0,357
|
0,364
|
0,371
|
|
1,20
|
0,378
|
0,386
|
0,393
|
0,400
|
0,408
|
0,415
|
0,423
|
0,431
|
0,438
|
0,446
|
|
1,30
|
0,454
|
0,462
|
0,171
|
0,479
|
0,487
|
0,496
|
0,504
|
0,513
|
0,521
|
0,530
|
|
1,40
|
0,539
|
0,548
|
0,557
|
0,566
|
0,575
|
0,584
|
0,594
|
0,603
|
0,613
|
0,623
|
|
1,50
|
0,632
|
0,642
|
0,652
|
0,662
|
0,672
|
0,682
|
0,692
|
0,703
|
0,713
|
0,724
|
|
1,60
|
0,734
|
0,745
|
0,756
|
0,767
|
0,778
|
0,789
|
0,800
|
0,811
|
0,823
|
0,834
|
|
1,70
|
0,846
|
0,857
|
0,860
|
0,881
|
0,893
|
0,905
|
0,917
|
0,929
|
0,911
|
0,953
|
|
1,80
|
0,966
|
0,978
|
0,991
|
1,004
|
1,016
|
1,029
|
1,042
|
1,055
|
1,069
|
1,082
|
|
1,90
|
1,095
|
1,109
|
1,122
|
1,136
|
1,150
|
1,163
|
1,177
|
1,191
|
1,205
|
1,220
|
|
2,00
|
1,234
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
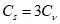
|
||||||||||
|
0,10
|
0,0022
|
0,0026
|
0,0031
|
0,0037
|
0,0043
|
0,0048
|
0,0055
|
0,0062
|
0,0070
|
0,0078
|
|
0,20
|
0,0085
|
0,0094
|
0,0104
|
0,0113
|
0,0122
|
0,0132
|
0,0143
|
0,0154
|
0,0165
|
0,0176
|
|
0,30
|
0,0188
|
0,0201
|
0,0214
|
0,0227
|
0,0240
|
0,0253
|
0,0267
|
0,0282
|
0,0297
|
0,0311
|
|
0,40
|
0,0326
|
0,0342
|
0,0359
|
0,0375
|
0,0391
|
0,0408
|
0,0425
|
0,0443
|
0,0461
|
0,0479
|
|
0,50
|
0,0497
|
0,0516
|
0,0535
|
0,0555
|
0,0574
|
0,0594
|
0,0614
|
0,0635
|
0,0656
|
0,0677
|
|
0,60
|
0,0698
|
0,0720
|
0,0742
|
0,0764
|
0,0786
|
0,0808
|
0,0832
|
0,0856
|
0,0879
|
0,0903
|
|
0,70
|
0,0926
|
0,0951
|
0,0976
|
0,100
|
0,103
|
0,105
|
0,108
|
0,110
|
0,113
|
0,116
|
|
0,80
|
0,118
|
0,121
|
0,124
|
0,127
|
0,129
|
0,132
|
0,135
|
0,138
|
0,141
|
0,144
|
|
0,90
|
0,147
|
0,150
|
0,153
|
0,156
|
0,159
|
0,162
|
0,165
|
0,168
|
0,171
|
0,174
|
|
1,00
|
0,177
|
0,181
|
0,184
|
0,187
|
0,191
|
0,194
|
0,197
|
0,201
|
0,204
|
0,208
|
|
1,10
|
0,211
|
0,215
|
0,218
|
0,222
|
0,225
|
0,229
|
0,232
|
0,236
|
0,240
|
0,243
|
|
1,20
|
0,247
|
0,251
|
0,255
|
0,258
|
0,262
|
0,266
|
0,270
|
0,274
|
0,277
|
0,281
|
|
1,30
|
0,285
|
0,289
|
0,294
|
0,298
|
0,302
|
0,306
|
0,311
|
0,315
|
0,319
|
0,323
|
|
1,40
|
0,327
|
0,332
|
0,336
|
0,340
|
0,345
|
0,349
|
0,354
|
0,358
|
0,363
|
0,367
|
|
1,50
|
0,372
|
0,376
|
0,381
|
0,386
|
0,390
|
0,395
|
0,400
|
0,404
|
0,409
|
0,414
|
|
1,60
|
0,419
|
0,424
|
0,428
|
0,433
|
0,438
|
0,443
|
0,448
|
0,453
|
0,458
|
0,463
|
|
1,70
|
0,468
|
0,474
|
0,479
|
0,484
|
0,489
|
0,495
|
0,500
|
0,505
|
0,511
|
0,516
|
|
180
|
0,521
|
0,527
|
0,532
|
0,538
|
0,543
|
0,549
|
0,555
|
0,560
|
0,566
|
0,572
|
|
1,90
|
0,578
|
0,584
|
0,589
|
0,595
|
0,600
|
0,606
|
0,612
|
0,618
|
0,624
|
0,630
|
|
2,00
|
0,636
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|

|
||||||||||
|
0,10
|
0,0022
|
0,0026
|
0,0031
|
0,0037
|
0,0043
|
0,0048
|
0,0055
|
0,0062
|
0,0069
|
0,0076
|
|
0,20
|
0,0083
|
0,0092
|
0,0101
|
0,0110
|
0,0119
|
0,0128
|
0,0138
|
0,0148
|
0,0159
|
0,0169
|
|
0,30
|
0,0180
|
0,0192
|
0,0203
|
0,0215
|
0,0227
|
0,0239
|
0,0252
|
0,0265
|
0,0279
|
0,0292
|
|
0,40
|
0,0305
|
0,0319
|
0,0334
|
0,0348
|
0,0363
|
0,0377
|
0,0392
|
0,0408
|
0,0423
|
0,0439
|
|
0,50
|
0,0454
|
0,0471
|
0,0488
|
0,0505
|
0,0522
|
0,0538
|
0,0556
|
0,0574
|
0,0592
|
0,0609
|
|
0,60
|
0,0627
|
0,0646
|
0,0665
|
0,0683
|
0,0702
|
0,0721
|
0,0741
|
0,0760
|
0,0780
|
0,0800
|
|
0,70
|
0,0820
|
0,0840
|
0,0861
|
0,0882
|
0,0903
|
0,0923
|
0,0946
|
0,0966
|
0,0989
|
0,101
|
|
0,80
|
0,103
|
0,105
|
0,108
|
0,110
|
0,112
|
0,114
|
0,117
|
0,119
|
0,121
|
0,124
|
|
0,90
|
0,126
|
0,128
|
0,131
|
0,133
|
0,136
|
0,138
|
0,141
|
0,143
|
0,146
|
0,148
|
|
1,00
|
0,151
|
0,153
|
0,156
|
0,158
|
0,161
|
0,163
|
0,166
|
0,169
|
0,171
|
0,174
|
|
1,10
|
0,177
|
0,179
|
0,182
|
0,185
|
0,188
|
0,190
|
0,193
|
0,196
|
0,199
|
0,201
|
|
1,20
|
0,204
|
0,207
|
0,210
|
0,213
|
0,216
|
0,219
|
0,222
|
0,224
|
0,227
|
0,230
|
|
1,30
|
0,233
|
0,236
|
0,239
|
0,242
|
0,245
|
0,248
|
0,251
|
0,254
|
0,258
|
0,261
|
|
1,40
|
0,264
|
0,267
|
0,270
|
0,273
|
0,276
|
0,279
|
0,283
|
0,286
|
0,289
|
0,292
|
|
1,50
|
0,296
|
0,299
|
0,320
|
0,305
|
0,309
|
0,312
|
0,315
|
0,319
|
0,322
|
0,325
|
|
1,60
|
0,329
|
0,332
|
0,336
|
0,339
|
0,342
|
0,346
|
0,349
|
0,353
|
0,356
|
0,360
|
|
1,70
|
0,363
|
0,367
|
0,370
|
0,374
|
0,377
|
0,381
|
0,384
|
0,388
|
0,392
|
0,395
|
|
1,80
|
0,399
|
0,403
|
0,406
|
0,410
|
0,414
|
0,417
|
0,421
|
0,425
|
0,429
|
0,432
|
|
1,90
|
0,436
|
0,440
|
0,444
|
0,447
|
0,451
|
0,455
|
0,459
|
0,463
|
0,467
|
0,471
|
|
2,00
|
0,474
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
Таблица Б.5
усеченного гамма-распределения
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
0,1
|
0,925
|
0,919
|
0,913
|
0,906
|
0,900
|
0,894
|
0,887
|
0,882
|
0,875
|
0,869
|
|
0,2
|
0,863
|
0,856
|
0,852
|
0,847
|
0,841
|
0,836
|
0,831
|
0,825
|
0,820
|
0,814
|
|
0,3
|
0,809
|
0,805
|
0,800
|
0,795
|
0,791
|
0,787
|
0,782
|
0,777
|
0,773
|
0,769
|
|
0,4
|
0,764
|
0,760
|
0,756
|
0,751
|
0,747
|
0,743
|
0,739
|
0,735
|
0,730
|
0,726
|
|
0,5
|
0,722
|
0,719
|
0,715
|
0,712
|
0,708
|
0,705
|
0,702
|
0,698
|
0,695
|
0,691
|
|
0,6
|
0,688
|
0,685
|
0,681
|
0,678
|
0,674
|
0,671
|
0,668
|
0,664
|
0,661
|
0,657
|
|
0,7
|
0,654
|
0,652
|
0,649
|
0,647
|
0,645
|
0,643
|
0,640
|
0,638
|
0,636
|
0,633
|
|
0,8
|
0,631
|
0,629
|
0,627
|
0,624
|
0,622
|
0,620
|
0,618
|
0,616
|
0,613
|
0,611
|
|
0,9
|
0,609
|
0,607
|
0,605
|
0,604
|
0,602
|
0,600
|
0,598
|
0,596
|
0,595
|
0,593
|
|
1,0
|
0,591
|
0,589
|
0,588
|
0,586
|
0,585
|
0,583
|
0,581
|
0,580
|
0,578
|
0,577
|
|
1,1
|
0,575
|
0,574
|
0,572
|
0,571
|
0,569
|
0,568
|
0,567
|
0,565
|
0,564
|
0,562
|
|
1,2
|
0,561
|
0,560
|
0,559
|
0,558
|
0,557
|
0,556
|
0,554
|
0,553
|
0,552
|
0,551
|
|
1,3
|
0,550
|
0,549
|
0,548
|
0,547
|
0,546
|
0,545
|
0,544
|
0,543
|
0,542
|
0,541
|
|
1,4
|
0,540
|
0,539
|
0,538
|
0,538
|
0,537
|
0,536
|
0,535
|
0,534
|
0,534
|
0,533
|
|
1,5
|
0,532
|
0,531
|
0,530
|
0,530
|
0,529
|
0,528
|
0,528
|
0,527
|
0,526
|
0,526
|
|
1,6
|
0,526
|
0,525
|
0,525
|
0,524
|
0,524
|
0,523
|
0,522
|
0,522
|
0,521
|
0,521
|
|
1,7
|
0,520
|
0,520
|
0,519
|
0,519
|
0,518
|
0,518
|
0,518
|
0,517
|
0,517
|
0,516
|
|
1,8
|
0,516
|
0,516
|
0,155
|
0,515
|
0,514
|
0,514
|
0,513
|
0,513
|
0,513
|
0,512
|
|
1,9
|
0,512
|
0,512
|
0,511
|
0,511
|
0,511
|
0,511
|
0,510
|
0,510
|
0,510
|
0,509
|
|
2,0
|
0,509
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
Таблица Б.6
изменчивости
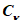 усеченного гамма-распределения
усеченного гамма-распределения
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
|
||||||||||
|
0,10
|
0,00050
|
0,00070
|
0,0090
|
0,00110
|
0,00130
|
0,00150
|
0,00170
|
0,00190
|
0,00210
|
0,00230
|
|
0,20
|
0,00250
|
0,00281
|
0,00321
|
0,0343
|
0,00374
|
0,00405
|
0,00436
|
0,00467
|
0,00498
|
0,00529
|
|
0,30
|
0,00560
|
0,00608
|
0,00656
|
0,00704
|
0,00752
|
0,00800
|
0,00848
|
0,00896
|
0,00944
|
0,00992
|
|
0,40
|
0,0104
|
0,0109
|
0,0114
|
0,0119
|
0,0124
|
0,0129
|
0,0135
|
0,0142
|
0,0148
|
0,0154
|
|
0,50
|
0,0161
|
0,0168
|
0,0176
|
0,0183
|
0,0191
|
0,0198
|
0,0206
|
0,0231
|
0,0220
|
0,0228
|
|
0,60
|
0,0235
|
0,0243
|
0,0250
|
0,0259
|
0,0267
|
0,0275
|
0,0282
|
0,0290
|
0,0298
|
0,0306
|
|
0,70
|
0,0314
|
0,0324
|
0,0328
|
0,0335
|
0,0342
|
0,0349
|
0,0358
|
0,0366
|
0,0375
|
0,0383
|
|
0,80
|
0,0392
|
0,0400
|
0,0409
|
0,0417
|
0,0426
|
0,0434
|
0,0444
|
0,0453
|
0,0463
|
0,0473
|
|
0,90
|
0,0482
|
0,0493
|
0,0503
|
0,0514
|
0,0524
|
0,0534
|
0,0545
|
0,0556
|
0,0568
|
0,0579
|
|
1,00
|
0,0590
|
0,0601
|
0,0613
|
0,0624
|
0,0636
|
0,0647
|
0,0659
|
0,0670
|
0,0682
|
0,0693
|
|
1,10
|
0,0704
|
0,0718
|
0,0731
|
0,0744
|
0,758
|
0,0771
|
0,0785
|
0,0799
|
0,0813
|
0,0828
|
|
1,20
|
0,0842
|
0,0856
|
0,0871
|
0,0886
|
0,0901
|
0,0916
|
0,0932
|
0,0948
|
0,0964
|
0,0980
|
|
1,30
|
0,0995
|
0,101
|
0,103
|
0,105
|
0,106
|
0,108
|
0,110
|
0,112
|
0,113
|
0,115
|
|
1,40
|
0,117
|
0,119
|
0,121
|
0,122
|
0,124
|
0,126
|
0,128
|
0,130
|
0,132
|
0,134
|
|
1,50
|
0,136
|
0,137
|
0,139
|
0,141
|
0,143
|
0,145
|
0,147
|
0,149
|
0,151
|
0,154
|
|
1,60
|
0,156
|
0,158
|
0,160
|
0,162
|
0,164
|
0,166
|
0,168
|
0,170
|
0,173
|
0,175
|
|
1,70
|
0,177
|
0,180
|
0,183
|
0,185
|
0,188
|
0,190
|
0,193
|
0,195
|
0,197
|
0,200
|
|
1,80
|
0,202
|
0,205
|
0,207
|
0,210
|
0,213
|
0,215
|
0,217
|
0,220
|
0,222
|
0,224
|
|
1,90
|
0,227
|
0,229
|
0,231
|
0,234
|
0,236
|
0,238
|
0,241
|
0,245
|
0,248
|
0,251
|
|
2,00
|
0,254
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
ТАБЛИЦЫ ЗНАЧЕНИЙ ПАРАМЕТРОВ РАСЧЕТНЫХ ФОРМУЛ
Таблица В.1
|
Значение
|
r
(1)
|
Коэффициенты
|
|||||
|
a
1
|
a
2
|
a
3
|
a
4
|
a
5
|
a
6
|
||
|
2
|
0
|
0
|
0,19
|
0,99
|
-0,88
|
0,01
|
1,54
|
|
0,3
|
0
|
0,22
|
0,99
|
-0,41
|
0,01
|
1,51
|
|
|
0,5
|
0
|
0,18
|
0,98
|
0,41
|
0,02
|
1,47
|
|
|
3
|
0
|
0
|
0,69
|
0,98
|
-4,34
|
0,01
|
6,78
|
|
0,3
|
0
|
1,15
|
1,02
|
-7,53
|
-0,04
|
12,38
|
|
|
0,5
|
0
|
1,75
|
1,00
|
-11,79
|
-0,05
|
21,13
|
|
|
4
|
0
|
0
|
1,36
|
1,02
|
-9,68
|
-0,05
|
15,55
|
|
0,3
|
-0,02
|
2,61
|
1,13
|
-19,85
|
-0,22
|
34,15
|
|
|
0,5
|
-0,02
|
3,47
|
1,18
|
-29,71
|
-0,41
|
58,08
|
|
|
|
r
(1)
|
Коэффициенты
|
|||||
|
b
1
|
b
2
|
b
3
|
b
4
|
b
5
|
b
6
|
||
|
0
|
0,03
|
2,00
|
0,92
|
-5,09
|
0,03
|
8,1
|
|
|
0,3
|
0,03
|
1,77
|
0,93
|
-3,45
|
0,03
|
8,03
|
|
|
0,5
|
0,03
|
1,63
|
0,92
|
-0,97
|
0,03
|
7,94
|
|
Несмещенную оценку коэффициента автокорреляции между смежными членами ряда
r
(1) определяют по формуле
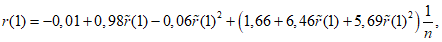 (В.1)
(В.1)
где смещенную оценку определяют по формуле
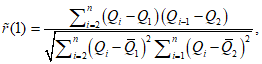 (В.2)
(В.2)
здесь
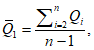
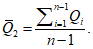 (В.3)
(В.3)
Таблица В.2
|
Параметры распределения
|
Нормальное распределение
|
Гамма-распределение
|
|
Среднее значение
|
R
xy
|
R
xy
|
|
Дисперсия
|
|
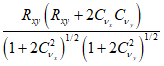
|
|
Стандартное отклонение
|
|

|
|
Коэффициент изменчивости
|
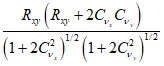
|
|
|
Коэффициент асимметрии
C
s
|
|
|
|
Отношение
|
|
|
Таблица В.3
вероятности превышения
|
Вероятность доверительного интервала, %
|
Число лет наблюдений
n
|
|||||||||||
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
110
|
120
|
|
|
Для наибольшего члена ряда наблюдений
|
||||||||||||
|
5
|
0,5
|
0,27
|
0,2
|
0,15
|
0,10
|
0,09
|
0,08
|
0,07
|
0,06
|
0,05
|
0,04
|
0,03
|
|
95
|
25,9
|
13,4
|
9,8
|
7,7
|
6,0
|
5,0
|
4,3
|
3,7
|
3,3
|
3,0
|
2,0
|
1,6
|
|
Для наименьшего члена ряда наблюдений
|
||||||||||||
|
5
|
74,1
|
87,0
|
90,0
|
92,2
|
94,0
|
95,0
|
95,7
|
96,3
|
96,7
|
97,0
|
97,8
|
98,5
|
|
95
|
99,50
|
99,72
|
99,81
|
99,86
|
99,90
|
99,91
|
99,92
|
99,93
|
99,94
|
99,95
|
99,96
|
99,97
|
Таблица В.4
|
Значения
|
Коэффициенты вариации
|
||||||||||||||
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
|
|
Трехпараметрическое гамма-распределение
|
|||||||||||||||
|
Метод приближенного наибольшего правдоподобия
|
|||||||||||||||
|
2
|
0,25
|
0,45
|
0,6
|
0,75
|
0,88
|
0,96
|
1,05
|
1,14
|
1,22
|
1,30
|
1,38
|
1,46
|
1,54
|
1,60
|
1,67
|
|
3
|
0,3
|
0,50
|
0,75
|
1,00
|
1,18
|
1,3
|
1,43
|
1,55
|
1,68
|
1,78
|
1,90
|
2,00
|
2,10
|
2,24
|
2,33
|
|
4
|
0,4
|
0,70
|
1,00
|
1,30
|
1,48
|
1,6
|
1,74
|
1,88
|
2,00
|
2,15
|
2,27
|
2,40
|
2,58
|
2,65
|
2,77
|
|
Метод моментов
|
|||||||||||||||
|
2
|
0,25
|
0,45
|
0,6
|
0,75
|
0,88
|
0,96
|
1,05
|
1,14
|
1,22
|
1,30
|
1,38
|
1,46
|
1,54
|
1,60
|
1,67
|
|
3
|
0,30
|
0,57
|
0,84
|
1,10
|
1,34
|
1,55
|
1,74
|
1,93
|
2,12
|
2,28
|
2,42
|
2,56
|
2,68
|
2,80
|
2,92
|
|
4
|
0,40
|
0,77
|
1,12
|
1,43
|
1,73
|
2,00
|
2,22
|
2,42
|
2,60
|
2,77
|
2,94
|
3,10
|
3,26
|
3,41
|
3,57
|
|
Биномиальное распределение
|
|||||||||||||||
|
Метод моментов
|
|||||||||||||||
|
2
|
0,25
|
0,45
|
0,6
|
0,75
|
0,88
|
0,96
|
1,05
|
1,14
|
1,22
|
1,30
|
1,38
|
1,46
|
1,54
|
1,6
|
1,67
|
|
3
|
0,28
|
0,52
|
0,75
|
0,97
|
1,19
|
1,35
|
1,59
|
1,63
|
1,96
|
2,14
|
2,31
|
2,49
|
2,66
|
2,84
|
3,01
|
|
4
|
0,30
|
0,61
|
0,91
|
1,20
|
1,49
|
1,66
|
2,04
|
2,30
|
2,56
|
2,82
|
3,09
|
3,35
|
3,62
|
3,89
|
4,15
|
Таблица В.5
и шероховатость русла водотока
|
Характеристика русла и поймы
|
m
|
m
р
, м/мин
|
|
Реки и водотоки со средними уклонами
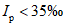 : чистые русла постоянных равнинных рек; русла периодически пересыхающих водотоков (сухих логов)
: чистые русла постоянных равнинных рек; русла периодически пересыхающих водотоков (сухих логов)
|
1/3
|
11
|
|
Извилистые, частично заросшие русла больших и средних рек; периодически пересыхающие водотоки, несущие во время паводка большое количество наносов
|
1/3
|
9
|
|
Сильно засоренные и извилистые русла периодически пересыхающих водотоков
|
1/3
|
7
|
|
Реки и периодически пересыхающие водотоки со средними уклонами
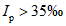
|
1/7
|
10
|
Таблица В.6
|
Характеристика поверхности склонов
|
Травяной покров склонов
|
||
|
Редкий или отсутствует
|
Обычный
|
Густой
|
|
|
Укатанная, спланированная грунтовая; такыровидные равнины
|
0,40
|
0,30
|
0,25
|
|
Без кочек, в населенных пунктах с застройкой менее 20%
|
0,30
|
0,25
|
0,20
|
|
Кочковатая, таежные завалы, а также в населенных пунктах с застройкой более 20%
|
0,20
|
0,15
|
0,10
|
Таблица В.7
y
=
Q
i
/
Q
р%
при различных коэффициентах
 и
k
s
и
k
s
|
x = t
i
/
t
П
|
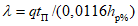
|
||||||||||||||||||||
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1,0
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
2,2
|
2,4
|
2,6
|
|
|
0,1
|
0,023
|
0,002
|
0
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,2
|
0,21
|
0,091
|
0,034
|
0,011
|
0,003
|
0
|
0
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,3
|
0,45
|
0,29
|
0,18
|
0,099
|
0,050
|
0,022
|
0,009
|
0,003
|
0,001
|
0
|
0
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,4
|
0,66
|
0,51
|
0,39
|
0,28
|
0,19
|
0,12
|
0,076
|
0,043
|
0,024
|
0,013
|
0,006
|
0,003
|
0,001
|
0
|
0
|
0
|
0
|
0
|
-
|
-
|
-
|
|
0,5
|
0,78
|
0,69
|
0,59
|
0,49
|
0,40
|
0,31
|
0,24
|
0,18
|
0,13
|
0,088
|
0,059
|
0,039
|
0,025
|
0,015
|
0,009
|
0,005
|
0,003
|
0,002
|
0
|
0
|
0
|
|
0,6
|
0,88
|
0,82
|
0,75
|
0,69
|
0,61
|
0,54
|
0,47
|
0,39
|
0,33
|
0,27
|
0,22
|
0,18
|
0,14
|
0,12
|
0,088
|
0,066
|
0,049
|
0,036
|
0,017
|
0,009
|
0,004
|
|
0,7
|
0,94
|
0,91
|
0,87
|
0,83
|
0,79
|
0,74
|
0,69
|
0,64
|
0,59
|
0,54
|
0,48
|
0,43
|
0,39
|
0,34
|
0,30
|
0,26
|
0,22
|
0,19
|
0,14
|
0,094
|
0,062
|
|
0,8
|
0,97
|
0,96
|
0,95
|
0,93
|
0,91
|
0,89
|
0,87
|
0,84
|
0,81
|
0,78
|
0,75
|
0,72
|
0,69
|
0,66
|
0,62
|
0,59
|
0,55
|
0,52
|
0,46
|
0,40
|
0,34
|
|
0,9
|
0,99
|
0,99
|
0,99
|
0,98
|
0,98
|
0,97
|
0,97
|
0,96
|
0,96
|
0,95
|
0,94
|
0,93
|
0,92
|
0,91
|
0,90
|
0,89
|
0,88
|
0,87
|
0,84
|
0,82
|
0,79
|
|
1,0
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
1,00
|
|
1,1
|
0,99
|
0,99
|
0,99
|
0,99
|
0,98
|
0,97
|
0,97
|
0,97
|
0,96
|
0,96
|
0,95
|
0,94
|
0,93
|
0,93
|
0,92
|
0,91
|
0,90
|
0,87
|
0,87
|
0,85
|
0,82
|
|
1,2
|
0,98
|
0,97
|
0,96
|
0,95
|
0,94
|
0,92
|
0,91
|
0,89
|
0,87
|
0,85
|
0,83
|
0,80
|
0,78
|
0,76
|
0,73
|
0,70
|
0,68
|
0,65
|
0,60
|
0,54
|
0,49
|
|
1,3
|
0,97
|
0,95
|
0,93
|
0,91
|
0,88
|
0,85
|
0,82
|
0,78
|
0,75
|
0,71
|
0,68
|
0,64
|
0,60
|
0,56
|
0,52
|
0,48
|
0,44
|
0,41
|
0,34
|
0,28
|
0,22
|
|
1,4
|
0,95
|
0,92
|
0,89
|
0,85
|
0,81
|
0,77
|
0,72
|
0,67
|
0,62
|
0,57
|
0,52
|
0,48
|
0,43
|
0,38
|
0,34
|
0,30
|
0,26
|
0,23
|
0,17
|
0,12
|
0,084
|
|
1,5
|
0,92
|
0,88
|
0,84
|
0,79
|
0,74
|
0,68
|
0,62
|
0,56
|
0,50
|
0,44
|
0,39
|
0,34
|
0,29
|
0,25
|
0,21
|
0,17
|
0,14
|
0,12
|
0,075
|
0,046
|
0,027
|
|
1,6
|
0,90
|
0,85
|
0,79
|
0,73
|
0,66
|
0,59
|
0,52
|
0,46
|
0,39
|
0,34
|
0,28
|
0,23
|
0,19
|
0,15
|
0,12
|
0,092
|
0,071
|
0,054
|
0,030
|
0,016
|
0,008
|
|
1,7
|
0,87
|
0,81
|
0,74
|
0,66
|
0,59
|
0,51
|
0,44
|
0,37
|
0,30
|
0,25
|
0,20
|
0,15
|
0,12
|
0,089
|
0,066
|
0,047
|
0,034
|
0,024
|
0,011
|
0,005
|
0,002
|
|
1,8
|
0,84
|
0,77
|
0,69
|
0,60
|
0,52
|
0,44
|
0,36
|
0,29
|
0,23
|
0,18
|
0,13
|
0,10
|
0,072
|
0,050
|
0,035
|
0,023
|
0,015
|
0,010
|
0,004
|
0,001
|
0
|
|
1,9
|
0,81
|
0,73
|
0,64
|
0,55
|
0,46
|
0,37
|
0,29
|
0,23
|
0,17
|
0,13
|
0,089
|
0,063
|
0,043
|
0,028
|
0,018
|
0,011
|
0,007
|
0,004
|
0,001
|
0
|
-
|
|
2,0
|
0,78
|
0,69
|
0,59
|
0,49
|
0,40
|
0,31
|
0,24
|
0,18
|
0,13
|
0,088
|
0,059
|
0,039
|
0,025
|
0,015
|
0,009
|
0,005
|
0,003
|
0,002
|
0
|
-
|
-
|
|
2,2
|
0,73
|
0,61
|
0,59
|
0,40
|
0,30
|
0,22
|
0,15
|
0,10
|
0,066
|
0,042
|
0,025
|
0,014
|
0,008
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2,4
|
0,67
|
0,54
|
0,42
|
0,32
|
0,22
|
0,15
|
0,096
|
0,058
|
0,034
|
0,019
|
0,010
|
0,005
|
0,002
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2,6
|
0,62
|
0,48
|
0,35
|
0,25
|
0,16
|
0,10
|
0,060
|
0,032
|
0,017
|
0,008
|
0,004
|
0,002
|
0,001
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2,8
|
0,57
|
0,42
|
0,29
|
0,19
|
0,12
|
0,068
|
0,036
|
0,018
|
0,008
|
0,004
|
0,001
|
0,001
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
3,0
|
0,53
|
0,37
|
0,24
|
0,15
|
0,086
|
0,045
|
0,022
|
0,010
|
0,004
|
0,002
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
3,5
|
0,43
|
0,26
|
0,15
|
0,079
|
0,037
|
0,016
|
0,006
|
0,002
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
4,0
|
0,34
|
0,19
|
0,092
|
0,042
|
0,016
|
0,005
|
0,002
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
5,0
|
0,21
|
0,091
|
0,034
|
0,011
|
0,003
|
0
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
6,0
|
0,13
|
0,044
|
0,012
|
0,003
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
8,0
|
0,052
|
0,010
|
0,002
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
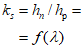
|
0,19
|
0,23
|
0,26
|
0,29
|
0,31
|
0,33
|
0,34
|
0,36
|
0,37
|
0,38
|
0,38
|
0,39
|
0,40
|
0,40
|
0,41
|
0,42
|
0,42
|
0,42
|
0,43
|
0,43
|
0,44
|
Таблица В.8
весеннего половодья
у
при различных коэффициентах
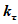
|
Время, ч
|
Относительные ординаты гидрографа при
|
|||||||||||
|
1
|
1,2
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
4,0
|
4,5
|
5,0
|
5,5
|
6,0
|
|
|
1
|
1,0
|
0,99
|
0,81
|
0,43
|
0,26
|
0,12
|
0,07
|
0,05
|
0,03
|
0,03
|
0,0
|
0,0
|
|
2
|
1,0
|
0,97
|
0,76
|
0,39
|
0,23
|
0,11
|
0,07
|
0,05
|
0,03
|
0,03
|
0,0
|
0,0
|
|
3
|
1,0
|
0,94
|
0,71
|
0,36
|
0,21
|
0,11
|
0,07
|
0,05
|
0,03
|
0,03
|
0,0
|
0,0
|
|
4
|
1,0
|
0,91
|
0,66
|
0,33
|
0,19
|
0,10
|
0,06
|
0,04
|
0,03
|
0,03
|
0,0
|
0,0
|
|
5
|
1,0
|
0,88
|
0,58
|
0,29
|
0,18
|
0,10
|
0,06
|
0,04
|
0,02
|
0,02
|
0,0
|
0,0
|
|
6
|
1,0
|
0,86
|
0,50
|
0,27
|
0,16
|
0,10
|
0,06
|
0,04
|
0,02
|
0,02
|
0,0
|
0,0
|
|
7
|
1,0
|
0,84
|
0,42
|
0,24
|
0,14
|
0,09
|
0,06
|
0,04
|
0,02
|
0,01
|
0,0
|
0,0
|
|
8
|
1,0
|
0,82
|
0,40
|
0,23
|
0,13
|
0,09
|
0,06
|
0,02
|
0,02
|
0,01
|
0,01
|
0,0
|
|
9
|
1,0
|
0,78
|
0,38
|
0,22
|
0,13
|
0,11
|
0,08
|
0,03
|
0,03
|
0,03
|
0,02
|
0,01
|
|
10
|
1,0
|
0,74
|
0,40
|
0,22
|
0,14
|
0,15
|
0,10
|
0,05
|
0,08
|
0,04
|
0,12
|
0,08
|
|
11
|
1,0
|
0,72
|
0,42
|
0,21
|
0,18
|
0,25
|
0,16
|
0,11
|
0,24
|
0,18
|
0,31
|
0,27
|
|
12
|
1,0
|
0,72
|
0,43
|
0,29
|
0,23
|
0,44
|
0,36
|
0,30
|
0,44
|
0,39
|
0,53
|
0,45
|
|
13
|
1,0
|
0,71
|
0,45
|
0,36
|
0,35
|
0,65
|
0,69
|
0,54
|
0,73
|
0,64
|
1,00
|
1,00
|
|
14
|
1,0
|
0,71
|
0,50
|
0,48
|
0,55
|
0,92
|
0,86
|
0,81
|
1,00
|
1,00
|
0,75
|
0,75
|
|
15
|
1,0
|
0,70
|
0,58
|
0,62
|
0,71
|
1,00
|
1,00
|
1,00
|
0,84
|
0,80
|
0,56
|
0,56
|
|
16
|
1,0
|
0,72
|
0,63
|
0,78
|
0,94
|
0,93
|
0,88
|
0,83
|
0,63
|
0,69
|
0,41
|
0,40
|
|
17
|
1,0
|
0,76
|
0,70
|
0,95
|
1,00
|
0,78
|
0,71
|
0,68
|
0,45
|
0,43
|
0,26
|
0,25
|
|
18
|
1,0
|
0,81
|
0,79
|
1,00
|
0,95
|
0,62
|
0,56
|
0,50
|
0,32
|
0,29
|
0,14
|
0,12
|
|
19
|
1,0
|
0,84
|
0,88
|
0,96
|
0,82
|
0,45
|
0,39
|
0,35
|
0,20
|
0,15
|
0,06
|
0,04
|
|
20
|
1,0
|
0,88
|
0,98
|
0,87
|
0,69
|
0,33
|
0,25
|
0,21
|
0,11
|
0,08
|
0,03
|
0,01
|
|
21
|
1,0
|
0,90
|
1,00
|
0,77
|
0,54
|
0,25
|
0,18
|
0,14
|
0,07
|
0,05
|
0,02
|
0,0
|
|
22
|
1,0
|
0,94
|
0,98
|
0,66
|
0,44
|
0,18
|
0,14
|
0,10
|
0,04
|
0,03
|
0,01
|
0,0
|
|
23
|
1,0
|
0,99
|
0,93
|
0,57
|
0,35
|
0,15
|
0,10
|
0,06
|
0,04
|
0,03
|
0,01
|
0,0
|
|
24
|
1,0
|
1,00
|
0,87
|
0,50
|
0,30
|
0,13
|
0,08
|
0,05
|
0,04
|
0,03
|
0,0
|
0,0
|
Таблица В.9
|
Характеристика русел и пойм
|
|||
|
n
|
Равнинные реки
|
Полугорные и горные реки
|
Поймы
|
|
0,020
|
Прямолинейные русла канализированных рек в плотных грунтах с тонким слоем илистых отложений
|
-
|
-
|
|
0,025
|
Естественные земляные русла в благоприятных условиях, чистые, прямые, со спокойным течением
|
Искусственные отводы русел, высеченные в скале
|
Ровная чистая пойма с низкой травой без сельскохозяйственного использования
|
|
0,030
|
Гравийно-галечные русла в тех же условиях
|
Гравийно-галечные русла в благоприятных условиях (чистые, прямые)
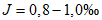
|
Ровная пойма под пашней без посевов и пастбищем с низкой травой
|
|
0,040
|
Сравнительно чистые русла постоянных водотоков с некоторыми неправильностями в направлениях струй, неровностями дна и берегов и влечением донных наносов
|
Земляные русла периодических водотоков (сухих логов) в благоприятных условиях. Правильные хорошо разработанные галечные русла в нижнем течении

|
Ровная пойма, занятая зрелыми полевыми культурами, пастбищем с высокой травой и вырубками без побегов, небольшое количество староречий и мелких просек
|
|
0,050
|
Значительно засоренные русла больших и средних рек, частично заросшие или каменистые, с неспокойным течением. Чистые русла периодических водотоков
|
Значительно засоренные каменистые русла с бурным течением. Периодические водотоки с крупногалечным покрытием ложа
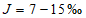
|
Пойма, поросшая редким кустарником и деревьями (весной без листвы), изрезанная староречьями
|
|
0,065
|
Скалистые русла больших и средних рек. Русла периодических водотоков, засоренные и заросшие
|
Галечно-валунные русла с бурным течением. Засоренные периодические водотоки
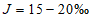
|
Пойма под редким кустарником и деревьями с листвой или вырубками с развивающейся порослью
|
|
0,080
|
Речные русла, значительно заросшие, с промоинами и неровностями дна и берегов
|
Валунные русла в средней и верхней частях бассейна и периодические водотоки с бурным течением и взволнованной водной поверхностью
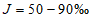
|
Поймы, покрытые кустарником средней и большой густоты (весной без листвы)
|
|
0,100
|
Русла рек, сильно заросшие, загроможденные стволами деревьев и валунами
|
Русла водопадного типа преимущественно в верховьях с крупновалунным ложем и бурным течением
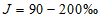
|
Поймы, занятые лесом при уровне ниже ветвей и кустарником средней и большой густоты с листвой
|
|
0,140
|
Реки болотного типа (заросли, кочки, во многих местах почти стоячая вода)
|
Русла с завалами из валунов и обломков скал и валунами
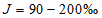
|
Поймы, покрытые лесом при затоплении ветвей и густым ивняком
|
|
0,200
|
-
|
Русла с завалами из валунов и обломков скал
|
Глухие, сплошь заросшие, труднопроходимые поймы таежного типа
|
ПОРЯДОК УТОЧНЕНИЯ ОРДИНАТ КРИВЫХ РЕДУКЦИИ ОСАДКОВ
И ПАРАМЕТРОВ ФОРМУЛЫ ПРЕДЕЛЬНОЙ ИНТЕНСИВНОСТИ
Г.1 Корректировку значений
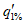 следует проводить поэтапно в такой последовательности:
следует проводить поэтапно в такой последовательности:
- на первом этапе
(первая строка таблицы Г.1)
для заданных значений бассейнового времени добегания
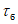 приводят ординаты кривых редукции осадков
приводят ординаты кривых редукции осадков
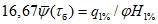 ;
;
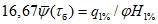 ;
;
- на втором этапе
(вторая строка таблицы Г.1)
по формуле, приведенной в
графе
"Вид расчета", для каждого из заданных значений бассейнового времени добегания
 рассчитывают значения руслового времени добегания
рассчитывают значения руслового времени добегания
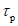 , мин;
, мин;
- на третьем этапе
(третья строка таблицы Г.1)
по формуле, приведенной в
графе
"Вид расчета", рассчитывают значения гидроморфометрического параметра
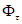 для каждого значения руслового времени добегания, приведенного в
строке 2
, и соответствующего ему значения ординаты кривой редукции осадков
для каждого значения руслового времени добегания, приведенного в
строке 2
, и соответствующего ему значения ординаты кривой редукции осадков
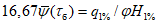 .
.
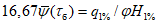 .
.
Таблица Г.1
в долях произведения (при
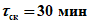 )
)
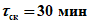 )
)
|
Номер этапа расчета
|
Значения для
A
1%
, для
|
||||||
|
5
|
10
|
20
|
40
|
...
|
1440
|
||

|
0,50
|
0,40
|
0,30
|
0,20
|
...
|
0,013
|
|

|
-
|
-
|
-
|
6,88
|
...
|
622
|
|
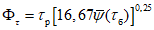
|
-
|
-
|
-
|
4,68
|
...
|
211
|
|
|
Примечание - При
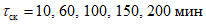 расчеты следует проводить в том же порядке, что и при
расчеты следует проводить в том же порядке, что и при
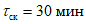 .
.
|
|||||||
Для перехода от расчетов, проведенных по
таблице Г.1
, к рекомендациям по выбору параметра
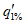 необходимо построить серию зависимостей
необходимо построить серию зависимостей
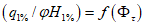 для каждого из принятых значений
для каждого из принятых значений
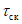 , по которым следует определить значения
, по которым следует определить значения
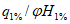 , соответствующие значениям
, соответствующие значениям
 .
.
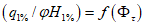 для каждого из принятых значений
для каждого из принятых значений
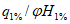 , соответствующие значениям
, соответствующие значениям
 .
.
Г.2 Уточнение рекомендаций по определению сборного коэффициента стока
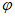 для равнинных рек необходимо проводить в следующем порядке:
для равнинных рек необходимо проводить в следующем порядке:
а) для условного водосбора с площадью, равной 10 км
2
, по
формуле (7.25)
определяют модуль максимального срочного расхода воды вероятности превышения
P
= 1% на основе использования гидрометрических данных гидрологически изученных рек. Для исследуемых рек, расположенных в тундровой и лесной зонах, в расчет включают водотоки с площадью водосбора менее 500 км
2
, для остальных - с площадью менее 300 км
2
:
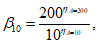 (Г.2)
(Г.2)
где
q
200
- то же, что и в
формуле (7.23)
;
б) для выбранных рек по
формуле (7.20)
рассчитывают продолжительность руслового добегания и по графику связи
 определяют среднее значение
определяют среднее значение
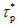 , соответствующее площади водосбора 10 км
2
;
, соответствующее площади водосбора 10 км
2
;
 определяют среднее значение
определяют среднее значение
в) по
формуле (7.29)
рассчитывают значение продолжительности бассейнового добегания
 , используя полученное значение
, используя полученное значение
 и рекомендации
Г.4
относительно назначения
и рекомендации
Г.4
относительно назначения
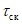 ;
;
г) по уточненным ординатам кривой редукции осадков определяют значение
 , соответствующее значению
, соответствующее значению
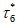 ;
;
 , соответствующее значению
, соответствующее значению
д) для каждого из выбранных водотоков рассчитывают коэффициент
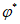 по формуле
по формуле
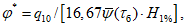 (Г.3)
(Г.3)
где
q
10
- то же, что и в
формуле (Г.1)
;
H
1%
- то же, что и в
формуле (7.25)
;
е) строят график связи
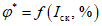 для выбранных рек с однородным (по типу и механическому составу) почвенным покровом, на основе использования которого уточняют рекомендации по назначению параметров
n
2
и
для выбранных рек с однородным (по типу и механическому составу) почвенным покровом, на основе использования которого уточняют рекомендации по назначению параметров
n
2
и
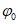 в
формуле (7.32)
.
в
формуле (7.32)
.
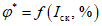 для выбранных рек с однородным (по типу и механическому составу) почвенным покровом, на основе использования которого уточняют рекомендации по назначению параметров
n
2
и
для выбранных рек с однородным (по типу и механическому составу) почвенным покровом, на основе использования которого уточняют рекомендации по назначению параметров
n
2
и
Г.3 Для горных рек корректировку рекомендаций по назначению сборного коэффициента стока
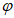 следует проводить на основе использования данных гидрологически изученных рек, для которых значения
следует проводить на основе использования данных гидрологически изученных рек, для которых значения
 определяют исходя из
формулы (7.25)
обратным путем. При этом необходимо исследовать степень влияния средней высоты водосбора, экспозиции склонов, а для районов, характеризующихся наличием многолетней мерзлоты, - также характера распространения многолетней мерзлоты (сплошной, прерывистой или островной).
определяют исходя из
формулы (7.25)
обратным путем. При этом необходимо исследовать степень влияния средней высоты водосбора, экспозиции склонов, а для районов, характеризующихся наличием многолетней мерзлоты, - также характера распространения многолетней мерзлоты (сплошной, прерывистой или островной).
Г.4 При отсутствии возможности уточнения параметров
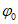 и
n
2
в
формуле (7.32)
допускается проводить уточнение только параметра
и
n
2
в
формуле (7.32)
допускается проводить уточнение только параметра
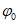 по формуле
по формуле
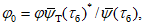 (Г.4)
(Г.4)
где
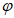 - сборный коэффициент стока;
- сборный коэффициент стока;
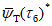 - уточненная ордината кривой редукции осадков, соответствующая заданной величине
- уточненная ордината кривой редукции осадков, соответствующая заданной величине

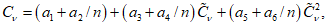
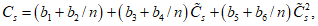
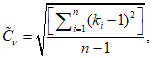
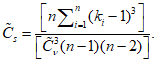



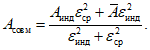
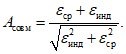
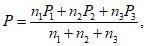
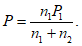
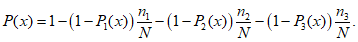
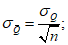
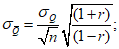

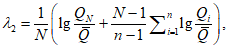

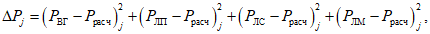
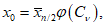

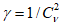 .
.
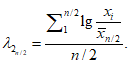
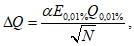
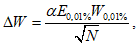
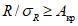 ;
;
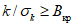 , (6.1)
, (6.1)
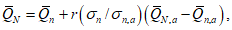
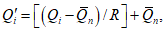
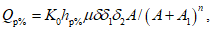
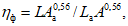
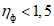 расчетное значение коэффициента
расчетное значение коэффициента
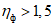 - по
- по

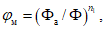

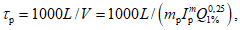

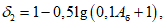
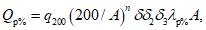

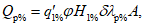
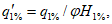
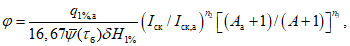
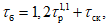
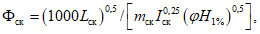
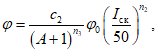



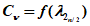 для вычисления коэффициента
для вычисления коэффициента